1.3 Сызықты электр схемаларын түрлендіру

Электр тізбектерін есептеген кезде, осы тізбектердің схемаларын қарапайым және есептеу үшін ыңғайлы схемаларға түрлендірген дұрыс, мысалы бірконтурлы немесе екі түйіні бар схемалар. Осындай түрлендірулерге тұрақты және айнымалы токтың сызықты тізбектері жатады. Төменде тұрақты ток тізбектеріне

қатысты түрлендірулер қарастырылған, бірақ сондай түрлендірулер айнымалы ток тізбегінде де қолданылады.

1.3.1 Элементтердің бірізді, параллель және аралас қосылуы

Бірізді қосылуы. 1.18 суретінде бейнеленген тізбектің барлық бірізді қосылған элементтері бойынша бір ғана I тогы өтеді. Элементтердегі осы токтан кернеулердің кемуі Ом заңы бойынша анықталады … .

1.18 Сурет

Тізбектің қыспақтарындағы кернеу Кирхгофтың екінші заңы бойынша есептеледі

U = U₁ + U₂ +…+ U_n = IR₁ + IR₂ +…+ IR_n = I , (1.7)

мұндағы R = – элементтері бірізді қосылған тізбектің қосынды (баламалы) кедергісі.

Баламалы тізбек 1.19 суретінде бейнеленген.

1.19 Сурет

Осы тізбектегі ток Ом заңы бойынша анықталады

.

Осыдан, бастапқы тізбектің жеке элементтеріндегі кернеудің кемуі осы элементтердің кедергілеріне пропорционал екенін көруге болады

. (1.8)

Резисторлардың бірізді қосылуы, тізбектің тогын шектеу үшін қолданылады, өйткені тізбектің кедергісі жоғарлайды.

1.20 Сурет − ЭҚК мен кедергілердің бірізді қосылуы

Е_бал = Е₁ – Е₂ + Е₃;

R_бал = R₁ + R₂ + R₃.

Параллель қосылуы. Өткізгіштіктері q₁, q₂, … q_n тең, 1.21 суретінде бейнеленген элементтердің параллель қосылуы кезінде, әр элементке жұмсалатын U кернеуі бірдей. Осы кезде тармақтарда I₁, I₂, … I_n токтары орын алады.

Параллель қосылуы кезінде екі түйін арасында көптеген тармақтар орналасады.

Кирхгофтың бірінші заңы бойынша тізбектің қосынды тогы

I = I₁ + I₂ +…+ I_n,

1.21 Сурет

немесе келесі формуламен есептелінеді

I=g₁U + g₂U +…+ g_nU = U* , (1.9)

мұндағы – k тармағының өткізгіштігі;

= g – элементтері параллель қосылған тізбектің баламалы өткізгіштігі.

Сондықтан тізбектің қосынды кедергісі келесіге тең

,

мұндағы – тізбектің кедергісі.

Осы формулаға 1.22 суретіндегі баламалы тізбек сәйкес келеді.

1.22 Сурет

1.21 суретінде бейнеленген бастапқы тізбектің тармақтарындағы ток өткізгіштіктерге пропорционал болады және келесі формулалармен есептелінеді

; . (1.10)

Екі тармағы бар тізбек үшін

немесе .

Сондықтан, осындай тізбектің жалпы кедергісі келесі формуламен есептелінеді

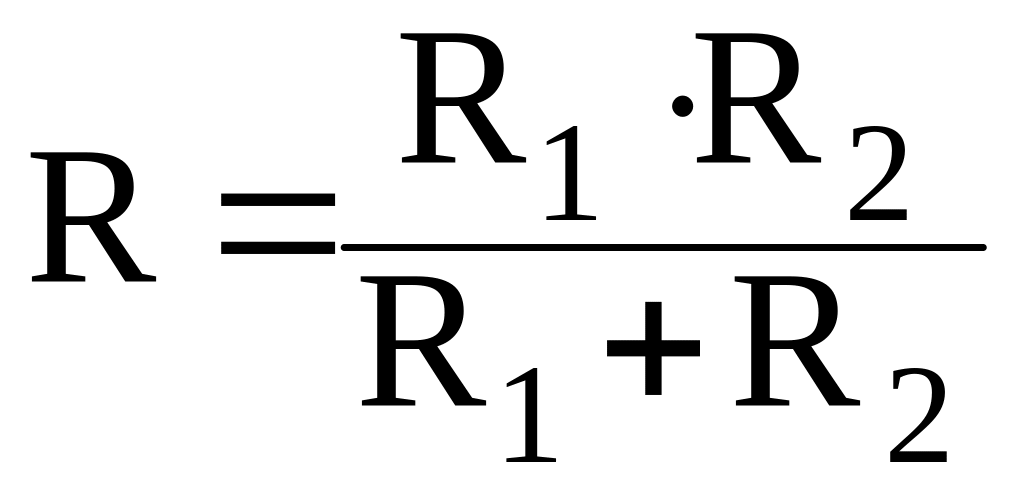. (1.11)

Тізбектің екі, шамалары бірдей параллель қосылған кедергілердің жалпы кедергісі екі есе аз болады.

Резисторлары параллель қосылған тізбектің жалпы (баламалы) кедергісі, тізбектің ең төмен кедергісінен аз болады; осындай қосылу тізбектің кедергісін төмендету үшін қолданылады (мысалы, жермен қосу жүйелерінде).

1.23 Сурет − Ток көздерінің параллель қосылуы

J_бал = J1 – J2 + J3.

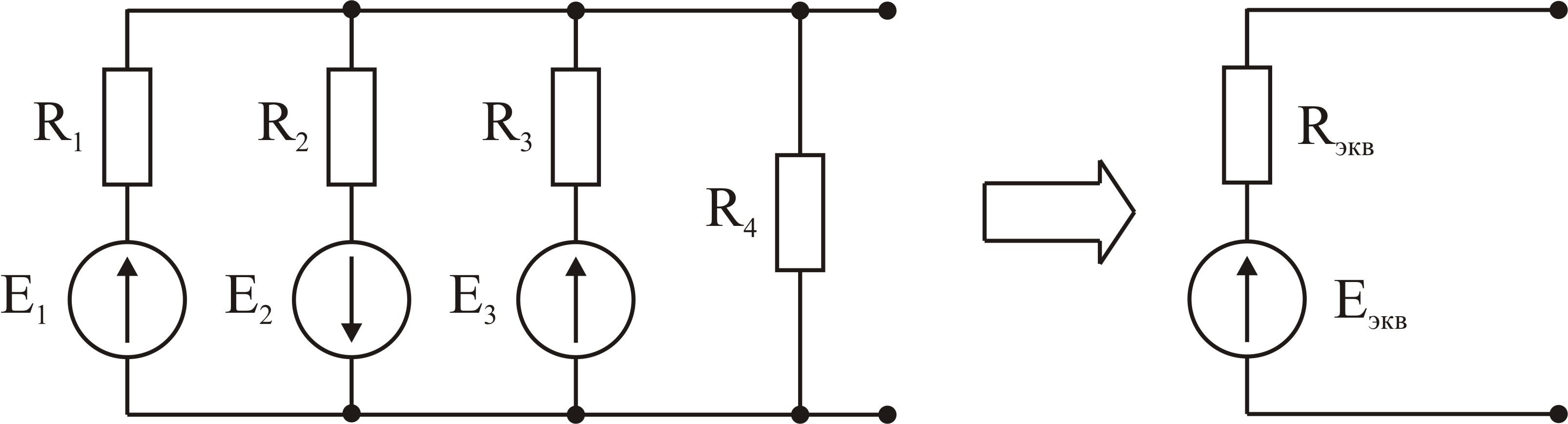
1.24 Сурет − ЭҚК мен кедергілерден тұратын тармақтардың

параллель қосылуы

Аралас қосылуы. Элементтері аралас қосылған 1.25 суретінде бейнеленген схеманы қарапайым схемаға түрлендіруге болады. Ол үшін параллель тарақтарды бір тармаққа, ал біріздіні – бір бөлікке ауыстыру керек.