2.9 Синусоидалы ток тізбегіндегі қуат

Электр тізбегінің кернеуі

болсын, ал тогы

.

Тізбекке келетін лездік қуат

, (2.24)

екі құраушыдан тұрады: тұрақты шамасынан және ток пен кернеудің жиілігімен салыстырғанда екі еселі жиілікке ие синусоидалы құраушыдан.

уақыт аралығында өзгерудің екі циклын жасайтын екінші құраушының орташа мәні нөлге тең. Сондықтан қарастырылатын тізбек бөлігіне келетін активті қуат

(2.25)

көбейткіші қуат коэфициенті деп аталады. (2.25)-тен активті қуат ток пен кернеудің нақты мәндерінің қуат коэфициентіне көбейтінді сияқты анықталатынын көреміз. бұрышы нөлге жақын болса, бірге жақын болады, сондықтан U мен I берілген мәндері кезінде қорек көзінен қабылдағышқа үлкен активті қуат беріледі.

Өндірістік электрқондырғыларының қуат коэффициентін көтеру маңызды технико-экономикалық міндет болып саналады.

(2.16) және (2.22) ескеріп активті қуаттың өрнегін келесідей түрлендіруге болады

.

Сонымен қатар активті қуат кернеу ( ) немесе токтың ( ) активті құраушылары арқылы анықталады

Лездік және активті қуаттардың келтірілген жалпы өрнектері жоғарыда қарастырылған жеке жағдайлар үшін қолданылады, олар (§ 2.4 қара), (§2.5 қара) және (§ 2.6).

Активті-реактивті тізбектің жалпы жағдайын қарастырайық, мысалы тізбек индуктивтілік пен кедергіден тұрсын; осы кезде

,

және

.

(2.24) сәйкес лездік қуат желі бойынша екі еселі жиілікпен тербеледі және уақыт өсінен

,

қалып тұрады (2.18 сурет).

2.18 Сурет − Активті-индуктивті тізбекке келетін қуат

және таңбалары бірдей болғандағы уақыт аралығында лездік қуат оң болады, энергия қорек көзінен қабылдағышқа барады және кедергіге сіңіріледі де индуктивтіліктің магнит өрісінде жиналады.

және таңбалары әртүрлі болғандағы уақыт аралығында лездік қуат кері болады және энергияның бір бөлігі қабылдағыштан қорек көзіне қайта оралады. 2.18 суретінен көретініміз, мерзімнің үлкен бөлігі кезінде лездік қуат оң таңбалы болады, сондықтан қисығының оң аймағы қысымының кері аймағынан басым болады. Нәтижесінде мерзім ішіндегі орташа қуат, яғни активті қуат, >0 болады.

Активті–сиымдылықты тізбек кезінде осындай жағдай қайталанады

Электр энергиясының көзі болып айнымалы токтың генераторлары саналатын электр жүйелеріндегі қуат генераторлары айналдыратын бірінші реттік қозғалтқыштар арқылы алынады. Синусоидалы тербеліс электронды немесе жартылайөткізгішті аспаптар арқылы жасалатын радиотехникада және электроникада қуат, электронды генераторларды немесе басқа түрлі құрылғыларды қоректендіретін тұрақты токтың көздері арқылы алынады.

Тізбектің нақты токтары мен кернеулердің көбейтіндісіне тең шама

(2.26)

тізбектің толық қуаты деп аталады және вольт-ампермен (ВА) өлшенеді. Айта кетсек, лездік қуаттың синусоидалы құраушысының амплитудасы (2.24) толық қуатқа тең.

(2.25) және (2.26) негізінде қуат коэффициенті активті қуаттың толық қуатқа қатынасы сияқты анықталады

Электр тізбектерін есептеген кезде және практикада реактивті қуат түсінігін қолданады және келесі формуламен есептейді

,

бұл реактивті токтың тұтыну (немесе шығару) өлшемі болып келеді.

Бұл қуат ВАр (вольт-ампер реактивті) деп аталатын бірлікпен өлшемденеді.

Сондықтан,

(2.16) мен (2.22) ескеріп реактивті қуаттың өрнегін келесідей түрлендіруге болады

Сонымен қатар, реактивті қуат токтың реактивті құраушысы ( ) немесе кернеудің реактивті құраушысы ( ) арқылы шығарылуы мүмкін

бұрышы үшін алдында қабылданған таңбалар ережесіне сәйкес, қалып тұрған ток кезде реактивті қуат оң болады (индуктивті жүктеме), ол озып тұратын ток кезде реактивті қуат кері болады (сиымдылықты жүктеме).

Индуктивтілік пен сиымдылыққа келтіретін реактивті қуат келесі түрде келтірілуі мүмкін

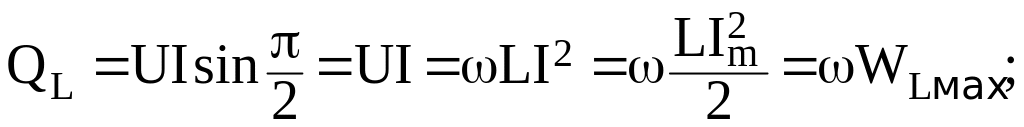
мұндағы және – индуктивтілікке және сиымдылықта жиналатын энергияның максималды мәндері.

Индуктивтілік пен сиымдылықтан тұратын тізбектің реактивті-қуат магниттік және электрлік өрістерде жиналатын энергияның максималды мәндердің айырымына пропорционал

(2.27)