
- •Расчет газодинамических параметров при течении газов в трубах, соплах и струях
- •6.05060101 «Теплоэнергетика»
- •Содержание
- •Введение
- •1 Общие указания и задание на курсовую работу
- •1.1 Исходные условия
- •1.2 Объем и содержание курсовой работы. Оформление пояснительной записки
- •1.3 Порядок сдачи курсовой работы и критерии оценок
- •2 Методические указания и теоретические основы
- •2.1 Расчет газопроводов. Порядок выполнения пневмогидравлического расчета
- •2.2 Потери давления при течении вязкого газа по каналу постоянного сечения
- •2.2.1 Изотермическое установившееся течение газа с трением по каналу постоянного сечения
- •2.2.2 Адиабатическое течение газа с трением в трубе постоянного сечения
- •2.3 Расчет кольцевых газопроводных сетей при изотермическом течении сжимаемого газа
- •2.4 Изоэнтропическое (адиабатное обратимое) течение газа в соплах
- •2.4.1 Выбор типа сопла и построение его профиля
- •2.4.2 Расчет параметров течения и основных геометрических размеров сопла
- •2.5 Адиабатическое течение вязкого газа в соплах
- •2.6 Расчет параметров свободных сверхзвуковых струй на основном участке (распределение скорости, концентрации и температуры газа в струе)
- •3 Контрольные вопросы
- •Приложение а
- •Приложение б
- •Приложение в
- •Приложение г
- •Приложение д
- •Приложение е
- •Приложение ж
- •Приложение и
- •П риложение к
2.4 Изоэнтропическое (адиабатное обратимое) течение газа в соплах
2.4.1 Выбор типа сопла и построение его профиля
При выборе
конструкции сопла для технологического
агрегата необходимо руководствоваться
значением полного перепада давления
![]() .
Давление газа в выходном сечении
.
Давление газа в выходном сечении
![]() согласно заданию должно быть равно
давлению в окружающей среде
согласно заданию должно быть равно
давлению в окружающей среде
![]() ,
т.е. реализуется расчетный режим истечения
и степень нерасчетности
,
т.е. реализуется расчетный режим истечения
и степень нерасчетности
![]() .
При
.
При
![]() условиям расчетного истечения
соответствует конструкция сопла Лаваля,
в противном случае (
условиям расчетного истечения
соответствует конструкция сопла Лаваля,
в противном случае (![]() )
– сужающееся (конфузорное) сопло или
цилиндрическое.
)
– сужающееся (конфузорное) сопло или
цилиндрическое.
2.4.2 Расчет параметров течения и основных геометрических размеров сопла
При адиабатном течении в соплах скорость течения газа велика и может быть выше скорости звука. Поэтому при таких больших скоростях (и адиабатном течении) теплообмен с окружающей средой отсутствует и, следовательно, не происходит потерь энергии в виде тепла в окружающую среду.
В этом случае при написании уравнения энергии (уравнения Бернулли) особо нет нужды учитывать работу сил трения, т.к. она сводится к преобразованию механической работы сил трения в тепловую энергию, а следовательно, не влечет к изменению содержания энергии в выделенном объеме газа.
Поэтому уравнение Бернулли можно представить как
![]() ;
(3.1)
;
(3.1)
или
![]() ,
,
где
![]() – показатель адиабаты;
– показатель адиабаты;
ср – изобарная теплоемкость, Дж/(кгК);
сv – изохорная теплоемкость, Дж/(кгК);
Р – абсолютное давление, Па;
ρ – плотность газа, кг/м3;
w – скорость газа, м/с;
i – энтальпия газа, Дж/кг;
Р0, ρ0, Т0, i0 – параметры торможения, т.е. параметры газа в точке, где скорость его адиабатически обращается в нуль;
![]() – удельная
потенциальная энергия давления, Дж/кг;
– удельная
потенциальная энергия давления, Дж/кг;
![]() – удельная
кинетическая энергия, Дж/кг;.
– удельная
кинетическая энергия, Дж/кг;.
![]() – удельная
внутренняя энергия, Дж/кг.
– удельная
внутренняя энергия, Дж/кг.
![]() – удельная тепловая
энергия (энтальпия) потока, Дж/кг;
– удельная тепловая
энергия (энтальпия) потока, Дж/кг;
![]() – удельная полная
энергия (полная энтальпия) потока или
энтальпия торможения, Дж/кг
– удельная полная
энергия (полная энтальпия) потока или
энтальпия торможения, Дж/кг
Следует отметить, что условие (3.1) соблюдается как вдоль оси потока, так и в любом поперечном сечении (живом) потока.
Уравнение Бернулли для двух сечений адиабатического потока сжимаемой вязкой жидкости обычно записывают в виде:
![]()
![]() .
.
Наряду с уравнениями Бернулли, которые записываются в разных формах, используют и уравнение адиабаты
![]() .
(3.2)
.
(3.2)
Разные формы
уравнения Бернулли обусловлены тем,
что течение газа характеризуется многими
параметрами и для каждой точки выполняется
уравнение состояния
![]() .
С учетом последнего и того, что скорость
звука в данной точке газа определяется
по формуле:
.
С учетом последнего и того, что скорость
звука в данной точке газа определяется
по формуле:
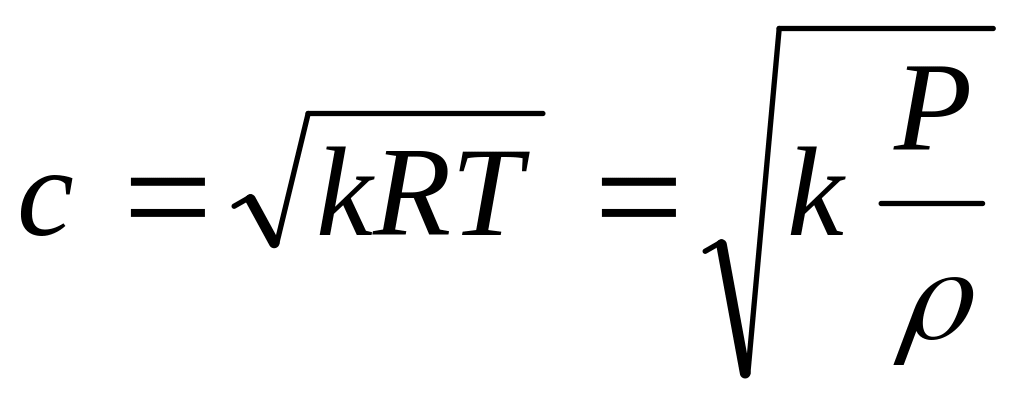 ,
(3.3)
,
(3.3)
уравнение Бернулли можно представить так:
![]() или
или
![]() ,
(3.4)
,
(3.4)
где с0 – скорость звука в покоящемся газе, м/с.
Из последних уравнений следует:
В потоке газа скорость звука изменяется вместе с его скоростью. При этом если скорость потока растет, то скорость звука в нем уменьшается.
В потоке газа могут существовать точки, в которых скорость звука равна скорости потока. Такие точки называются критическими. Параметры газа в этих точках тоже называются критическими.
Между критическими параметрами и параметрами торможения легко установить связь.
Так как критическая скорость выражается по формуле:
![]() .
(3.5)
.
(3.5)
Отсюда
![]() ;
(3.6)
;
(3.6)
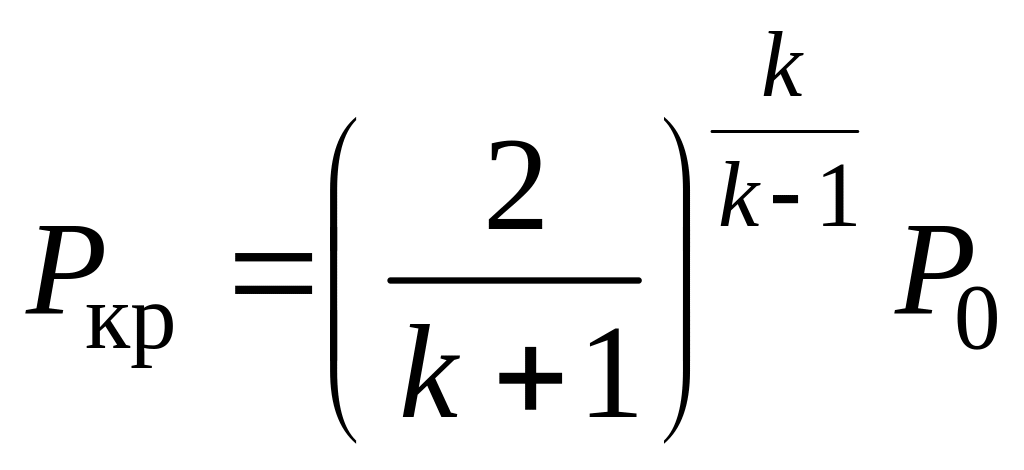 ;
(3.7)
;
(3.7)
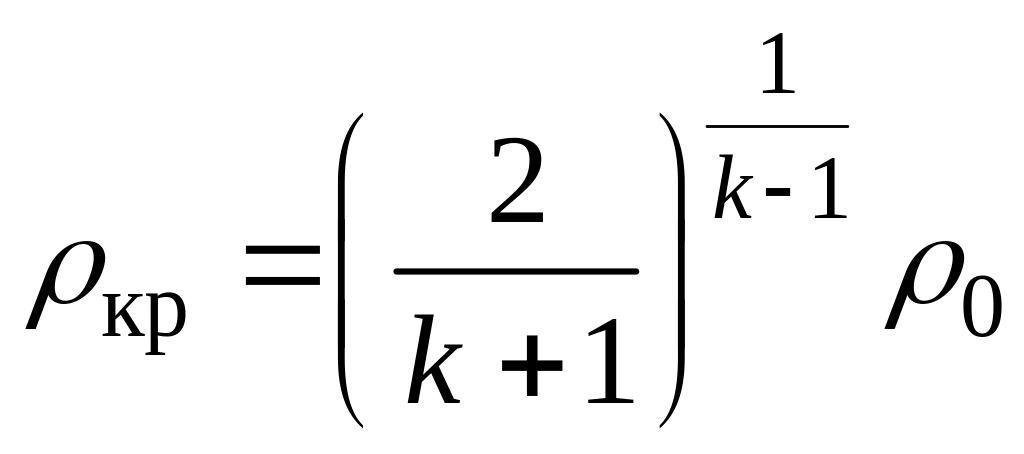 .
(3.8)
.
(3.8)
Так как при адиабатном течении температура торможения одинакова для всего потока, то и критическая скорость одинакова для всего потока. Поэтому приведенную скорость (коэффициент скорости) в этом случае использовать удобней.
Легко убедиться, что в критических точках М 1 и λ 1 и при M < 1 λ > M, а при M > 1 λ < M.
Вероятно, уравнение Бернулли можно привести к безразмерному виду и представить так
![]() (3.9)
(3.9)
или
![]() ,
(3.10)
,
(3.10)
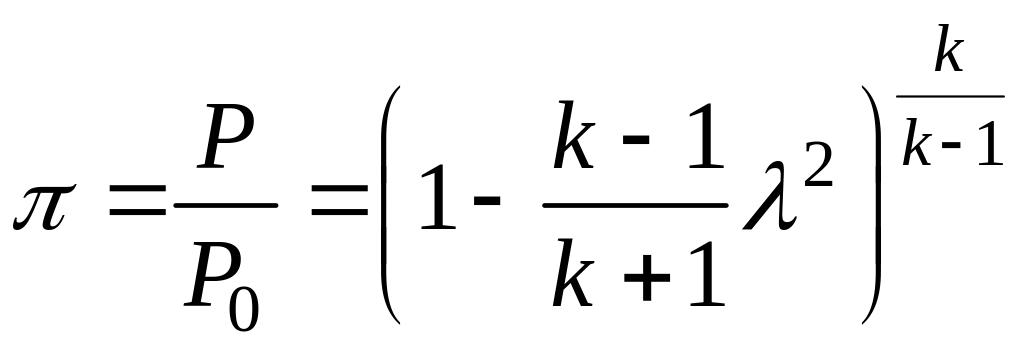 ,
(3.11)
,
(3.11)
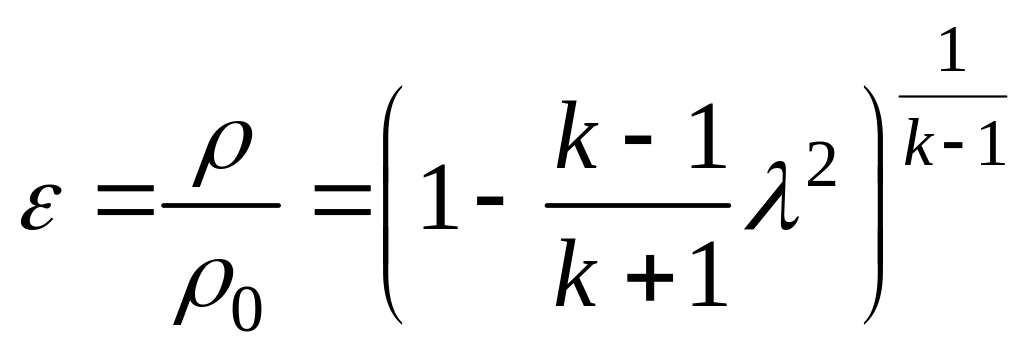 ,
(3.12)
,
(3.12)
а уравнение неразрывности – к виду
![]() ,
(3.13)
,
(3.13)
где τ, π, ε и q – основные газодинамические функции, для которых имеются таблицы ГДФ [11-13], облегчающие расчеты.
Таким образом, при отсутствии внешней механической работы и теплообмена через стенки выполняется условие постоянства температуры торможения по пути потока. Уместно заметить, что при изоляции газа от окружающей среды при помощи стенок каналов трение влияет не на температуру торможения Т0, а на термодинамическую температуру Т, повышая ее за счет уменьшения кинетической энергии, что соответствует закону сохранения энергии.
Полное давление торможения будет оставаться постоянным при отсутствии внутреннего трения и постоянства энтропии. В сугубо теоретическом, изоэнтропическом процессе (dS 0)
dP0 0
и давление торможения
![]() .
.
В адиабатических и изоэнтропических течениях температура торможения Т0 служит для оценки общей энергии всех видов движений, а давление торможения Р0 – для оценки механического движения.
Ниже приводится пример типового конструктивного расчета сопел Лаваля (рис.2.2) для невязкого (адиабатного обратимого) течения аналитическим способом и с помощью таблиц газодинамических функций (ТГФ).
Пример расчёта сопла Лаваля в предположении изоэнтропного процесса течения.
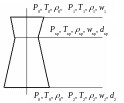 Рисунок
2.2 – Схема сопла Лаваля с характерными
термогазодинамическими параметрами
Рисунок
2.2 – Схема сопла Лаваля с характерными
термогазодинамическими параметрами
Давление газа (кислород), измеренное манометром на входе в конические сопла Лаваля, число которых z 4, составило 1,48 МПа, температура в потоке 303 К, скорость 54,3 м/с при массовом расходе 9,4045 кг/с. Определить параметры течения газа (Р, Т, , w, М, , I, Iизб, F, d) в критическом и выходном сечениях, размеры этих сечений и длину диффузора конического сопла, если угол наклона образующей диффузора сопла 6о. Давление в атмосфере принять равным 0,102 МПа. Показатель адиабаты газа k 1,4.
Решение.
Для удобства расчётов параметры на входе в сопло будем обозначать индексом 1, в критическом сечении индексом «кр», на выходе индексом 2:
Режим течения считается расчётным, если давление в выходном сечении и в окружающей среде равны: Р2 Рокр.ср.
Расчёты сопла выполним двумя способами.
I. Аналитический способ расчёта.
Предварительно определяем параметры заторможенного потока Т0, Р0, 0, критическую скорость звука акр, затем плотность газа 1 и местную скорость звука а1 в сечении 1:
![]()
![]()
![]()
![]()
![]()
![]()
Проверяем
условие
![]() :
:
![]() ,
,
т.е. перепад давлений сверхкритический, что позволяет получать сверхзвуковые скорости истечения из сопла Лаваля. При докритическом перепаде сверхзвуковое истечение невозможно.
Параметры (температура, скорость, плотность и давление) в критическом сечении:
![]()
![]() ;
;
![]()
![]()
Проверка:
![]()
Площадь, диаметр (одного из 4-х сопел) и полный импульс в критическом сечении:
![]()
![]()
![]()
Параметры (температура и плотность) в выходном сечении:
![]()
![]()
Скорость, площадь, диаметр сопла, полный и избыточный импульс в этом сечении:

![]()
![]()
![]()
![]()
где приведенная скорость и число Маха:
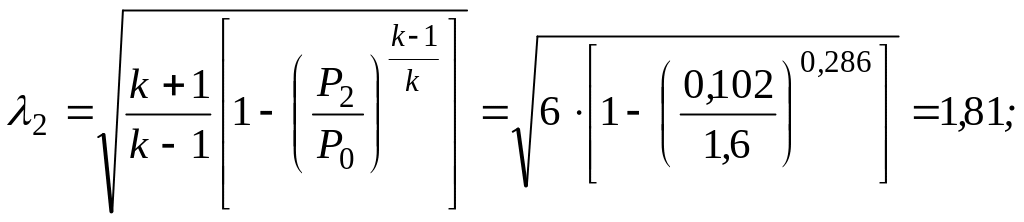

Длина расширяющейся части сопла составляет:
![]()
II. Расчёт с помощью таблиц газодинамических функций [13].
Полное давление
и плотность на входе в сопло рассчитываем,
предварительно определив по
![]() в ТГФ [13] для
k
1,4 приведенное давление
в ТГФ [13] для
k
1,4 приведенное давление
![]() и приведенную плотность
и приведенную плотность
![]() на
входе в сопло, откуда
на
входе в сопло, откуда
![]() МПа;
МПа;
![]()
Параметры в критическом сечении находим в ТГФ при Мкр кр 1 для k 1,4:
![]()
![]()
![]()
Параметры в выходном
сечении (температуру и плотность газа)
рассчитываем, предварительно определив
газодинамическую функцию приведенного
давления
![]() ,
по которой находим в ТГФ функции (2)
и (2):
,
по которой находим в ТГФ функции (2)
и (2):
![]()
![]() затем
соответственно приведенную скорость,
число Маха, функции приведенного расхода
и приведенного импульса:
затем
соответственно приведенную скорость,
число Маха, функции приведенного расхода
и приведенного импульса:
![]()
![]() .
.
Тогда величина скорости на выходе из сопла составит
![]() ,
,
площадь и диаметр выходного сечения, полный и избыточный импульс:
![]()
![]()
![]()
![]() .
.
