2.2.2 Адиабатическое течение газа с трением в трубе постоянного сечения

В отличие от изотермического, адиабатическое течение протекает без теплообмена с окружающей средой, т.е. dq  0, и температура газа зависит от местной скорости потока. Температура торможения в этих условиях не изменяется: T₀  const. Полное давление (давление торможения) вдоль потока не является постоянной, причем в конце трубопровода полное давление меньше из-за наличия потерь.

При установившемся течении в трубе постоянного сечения при наличии трения, используем закон обращения воздействий [1,3], связывающее изменение скорости вдоль трубы постоянного сечения на участке 1-2 с работой сил трения

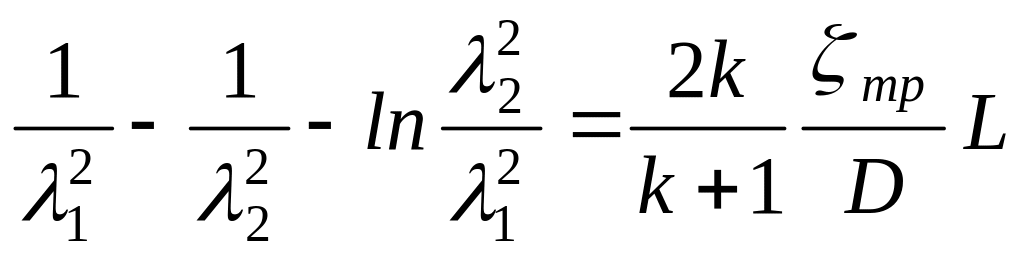(2.8)

где ₁ – значение приведенной скорости в начале трубы;

₂ – значение приведенной скорости потока в произвольном сечении трубы на расстоянии L от начала трубопровода.

Уравнение (2.8) можно представить, используя подстановку , в виде

(2.9)

Использование функции , которая приводится в некоторых таблицах газодинамических функций (ТГФ) (например, [12, 13]), ускоряет процесс расчетов. С помощью выражений (2.8) и (2.9) можно определить значение коэффициента скорости (и скорости) потока в произвольном сечении трубы, если известны коэффициент скорости ₁ (или скорость w₁) в начале трубопровода, диаметр трубопровода D, коэффициент трения  и показатель адиабаты k.

Из уравнения неразрывности и уравнения состояния с учетом постоянства поперечного сечения канала и температуры торможения Т₀  const следует зависимость плотности газа от скорости (и приведенной скорости ): , т.е.

. (2.10)

Давление и полное давление газа в конце участка на расстоянии L от начала трубопровода равно

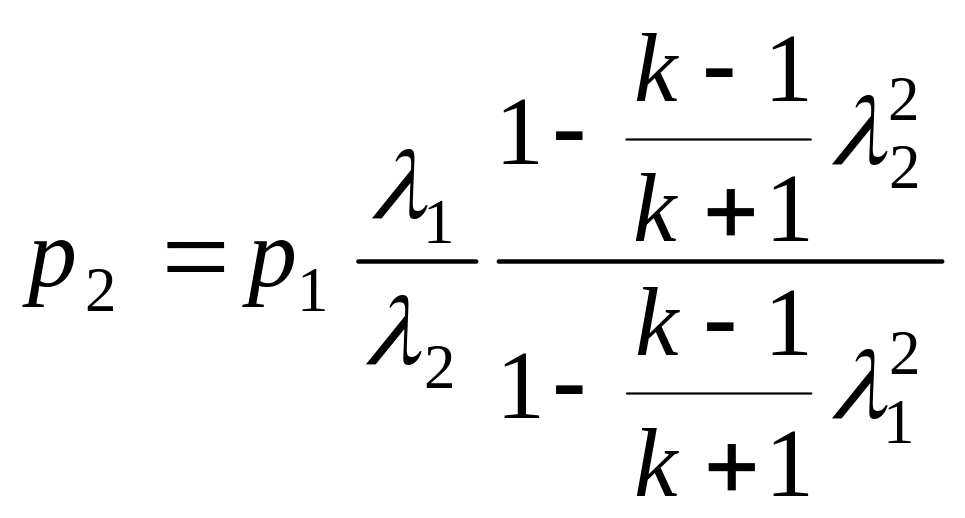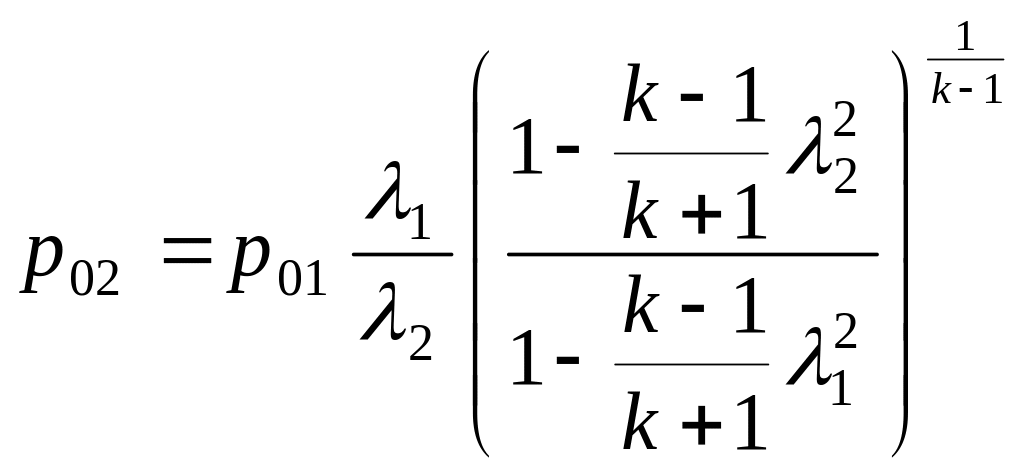, (2.11)

Пример расчета потерь давления из-за трения о стенки канала при адиабатном течении газа в трубопроводе постоянного сечения. Давление воздуха (молекулярная масса  = 28,97 кг/кмоль) на входе участка канала постоянного сечения длиной l = 0,15 м и диаметром D = 100 мм составляет 6 ата. Определить давление газа на выходе из канала, если расход газа при температуре t = 20⁰С (н.у.) в нем составляет V_н.у = 600 м³/мин. Процесс течения – адиабатный. Труба стальная нормальная (эквивалентная высота выступов шероховатости  = 1 мм).

Решение. Из выражения (2.12) можно определить давление газа на выходе из трубопровода

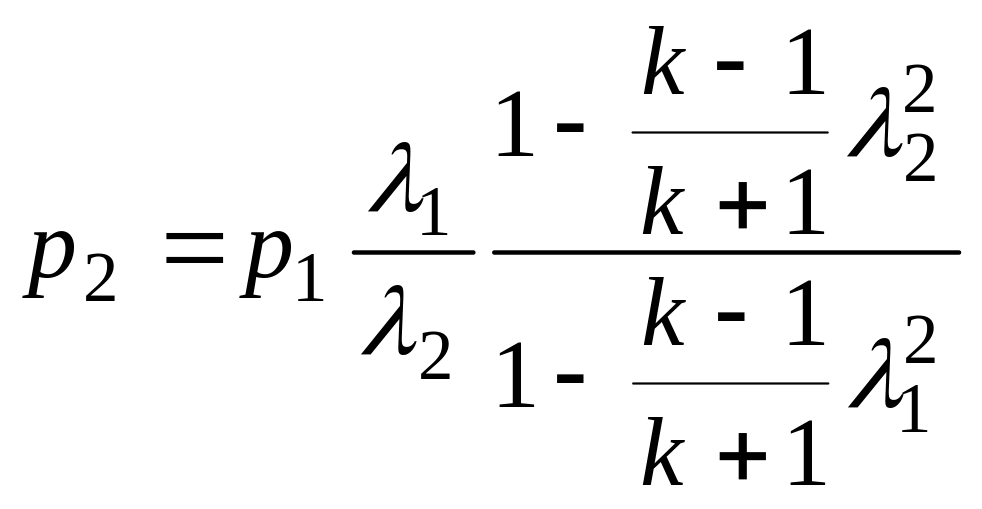
Приведенная скорость  на входе в трубопровод

.

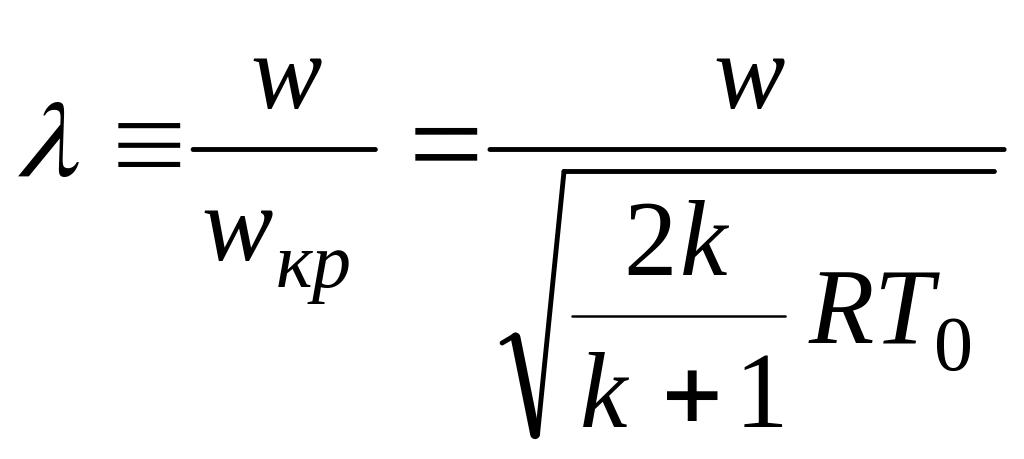Скорость движения газа в начале трубопровода

,

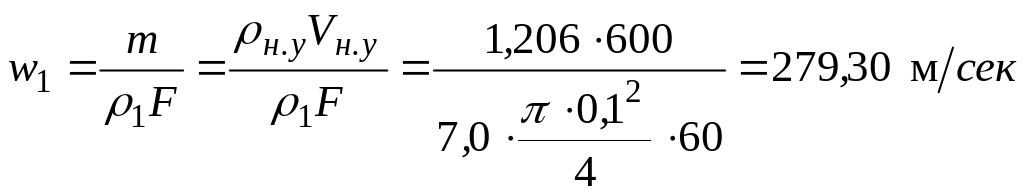где плотность газа при н.у.

.

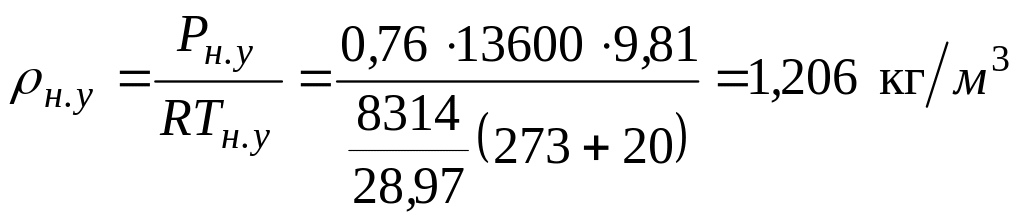Плотность движущегося газа в начальном сечении трубопровода

,

при массовом его расходе

.

Число Рейнольдса потока в начале участка трубопровода

,

где коэффициент динамической вязкости определен по Приложению Г с помощью метода линейной интерполяции по формуле

Таким образом, режим течения турбулентный и соотношение , т.е. трубопровод не «гидравлически гладкий», а т.к. величина, исходя из данных табл. Д1 (Приложение Д), , то коэффициент Дарси определим из выражения, представленного в Приложении Д

,

где  – коэффициент формы, учитывающий профиль поперечного сечения трубопровода. Для круглого сечения  = 1.

Из соотношения (Приложение Д) толщина ламинарного пограничного слоя

что меньше высоты выступов шероховатости и область сопротивления – квадратичная зона.

Температура заторможенного газа

.

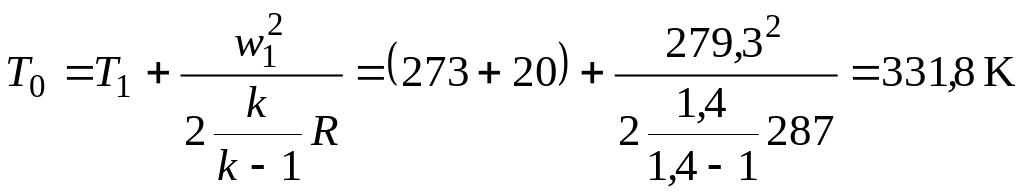Приведенная скорость

.

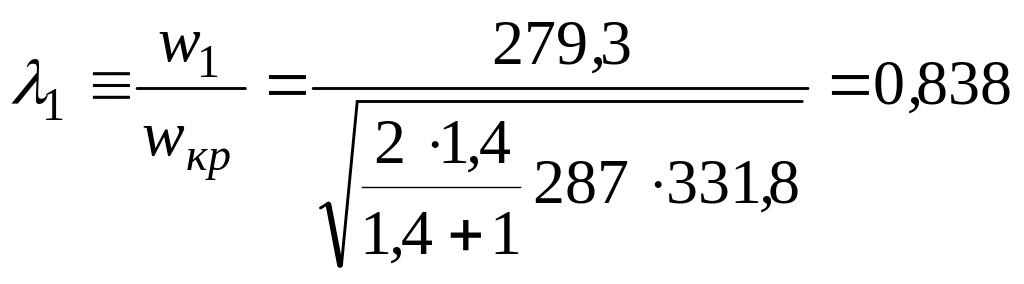Приведенную скорость ₂ на выходе из участка трубопровода определим методом последовательных приближений пренебрегая в первом приближении членом, содержащим логарифм отношения квадратов приведенных скоростей . Тогда

.

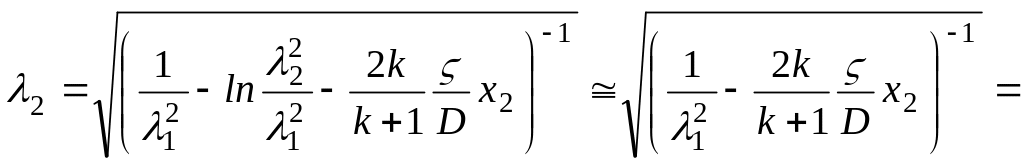
После второго и третьего приближений, уже не пренебрегая вторым членом в предыдущем уравнении, получим соответственно 0,8706 и 0,8815; четвертого и пятого – 0,8902 и 0,8972; шестого и седьмого – 0,9030 и 0,9077; далее – 0,9116; 0,9149; 0,9176; 0,920; 0,9220.

Окончательно получим ₂ = 0,9342.

Тогда статическое давление в конце участка трубопровода равно

.

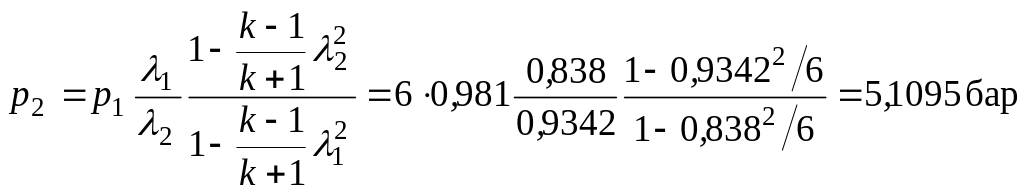Полное давление газа в этом сечении

.

Полное давление газа на входе в канал

.

Коэффициент восстановления полного давления   Р₀₂/Р₀₁ = 0,9734.

Расчет приведенной скорости ₂ в конце трубопровода по известной приведенной скорости в начале трубопровода можно упростить, используя для расчета таблицы газодинамических функций [12,13].

По ₁ = 0,838 определим, интерполируя значения по [13] (табл. 8), функцию ₁ = 1,0728.

Тогда

По значению ₂ = 1,0119 из ТГФ [13] (табл. 8) находим ₂ = 0,9324.

Остальные параметры определяются аналогично приведенному выше решению.