Лекція 6т розрахунок електричних мереж за втратою напруги

План лекції

1. Спад і втрата напруги в мережах змінного струму.

2. Розрахунок електричних мереж трифазного струму при сталому перерізі проводів магістралі за допустимою втратою напруги.

3. Перевірка електричної мережі на коливання напруги при пуску електричних двигунів.

4. Вплив відхилень напруги на роботу споживачів електричної енергії. Допустимі відхилення напруги.

5. Вплив елементів електричної мережі на відхилення напруги.

6. Визначення допустимої втрати напруги за таблицею відхилень.

Література: 2. c. 114-167; 3. с. 92-153; 4 с.90-156; 5 с.80-144; 6 с.70-118; 8 с.42-71; 9 с.258-288; 10 с.59-74; с.90-98.

1. Спад і втрата напруги в мережах змінного струму

Р озглянемо лінію трифазного змінного струму із навантаженням в кінці (рисунок 6.1, а). Вважатимемо, що навантаження усіх трьох фаз однакові. В цьому випадку трифазну лінію можна зобразити у вигляді однієї лінії (рисунок 6.1, б) і вести розрахунок для фазних напруг та струмів а потім перейти до їх лінійних значень.

а б

Рисунок 6.1 – Одна фаза трифазного струму із симетричним навантаженням в кінці: а – розгорнута схема; б – однолінійна схема.

На рисунку 6.1 прийняті наступні позначення: та – фазні напруги, відповідно, на початку і в кінці лінії, – струм навантаження,

соs  ₂ – коефіцієнт потужності навантаження, r – активний опір проводу, х – індуктивний опір проводу, z_нав – опір навантаження.

Струм, що проходить по провіднику, створює в ньому спад напруги. Тому напруга в кінці лінії відрізняється від напруги на її початку. Вектор спаду напруги в активному опорі збігається за напрямом із вектором струму, а вектор спаду напруги в індуктивному опорі випереджає вектор струму на 90⁰. Тому, в загальному випадку, вектор напруги в кінці лінії відрізняється від вектора напруги на початку лінії не лише за значенням, а й за напрямом.

Для запропонованої схеми побудуємо векторну діаграму (рисунок 6.2). Відкладаємо вектор напруги на початку лінії Під кутом  ₁ до нього відкладаємо вектор струму . Щоб дістати вектор напруги в кінці лінії необхідно від напруги на початку лінії відняти спад напруги в ній:

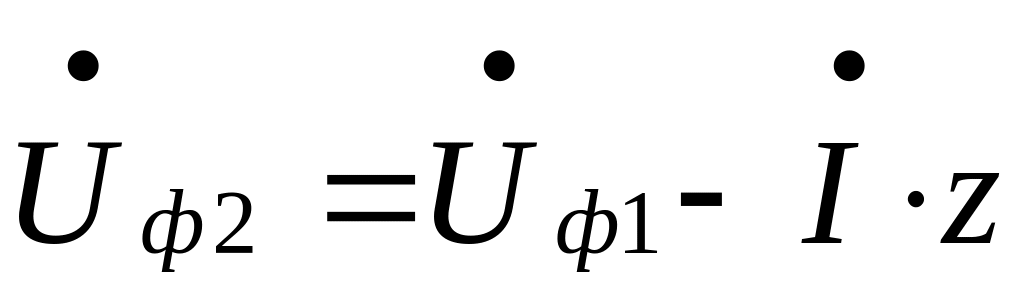. (6.1)

Для цього з кінця вектора напруги (0 a) паралельно вектору струму , але в протилежному напрямку відкласти вектор спаду напруги в активному опорі (a b), а під кутом 90⁰ до нього відкласти вектор спаду напруги в реактивному опорі (b c). Вектор (а с) і буде спадом напруги в повному опорі магістралі. Сполучивши точку 0 з точкою с отримаємо вектор напруги в кінці лінії (0 с).

Геометрична різниця між вектором напруги на початку і в кінці лінії називається спадом напруги:

. (6.2)

Якщо в напрямку вектора (0 a) відкласти значення вектора

напруги в кінці лінії (0 d), то матимемо відрізок a d – алгебрагічну різницю. Алгебрагічну різницю між напругою на початку лінії і в кінці називають втратою напруги:

. (6.3)

Рисунок 6.2 – Векторна діаграма для однієї фази трифазної лінії із навантаженням в кінці

Спад напруги можна розглядати не лише як суму його активної і реактивної складових. Опустивши з точки с перпендикуляр на напрямок вектора (0 a), із трикутника а е с матимемо:

. (6.4)

Відрізок а е називають поздовжньою складовою спаду напруги і позначають .

Відрізок е с називають поперечною складовою спаду напруги і позначають .

Опустивши перпендикуляр з точки b на вектор (0 a), і побудувавши прямокутник e g b f , матимемо:

. (6.5)

. (6.6)

Міжфазна складова напруги більша від фазної в рази, тому для поздовжньої складової міжфазної (лінійної) напруги можна записати:

, (6.7)

а для поперечної складової міжфазної (лінійної) напруги:

, (6.8)

або

, (6.9)

. (6.10)

Якщо навантаження задано у вигляді потужності, тоді:

; ; .

Увівши значення потужності в рівняння (6.9) та (6.10), матимемо:

, (6.11)

. (6.12)

Якщо магістраль живить кількох споживачів, то рівняння (6.9) та (6.10) приймуть вигляд:

, (6.13)

, (6.14)

а рівняння (6.11) та (6.12) – вигляд:

(6.15)

(6.16)

Для споживачів значення має не фаза, а абсолютне значення напруги, тому мережі розраховують не за спадом, а за втратою напруги.

З векторної діаграми (рисунок 6.2) видно, що за значенням втрата напруги відрізняється від поздовжньої складової спаду напруги на незначний за довжиною відрізок e d. Тому, для практичних розрахунків, в електричних мережах напругою до 35 кВ включно втрату напруги прирівнюють поздовжній складовій спаду напруги:

(6.17)

Похибка від такого припущення не перебільшує 5 %. Лінійна втрата напруги при цьому, якщо  ₂ =  :

, (6.18)

або

. (6.19)