5) Розкладання в ряд Фур’є функції на відрізку

Те, що за основній відрізок задання функцій, що розкладаються в тригонометричний ряд Фур’є, брали , є дуже зручним, але не принциповим. В багатьох теоретичних або практичних задачах доводиться мати справу з розкладаннями в тригонометричний ряд Фур’є в будь-якому відрізку .

Перехід від до можна здійснити зсувом початкового відрізку вздовж осі Ох і зміною масштабу по цій осі.

Зокрема, система тригонометричних функцій , є ортонормованою не тільки на , але й на будь-якому відрізку

Для коефіцієнтів Фур’є функції на маємо:

; (9)

;

Оскільки система тригонометричних функцій є ортонормованою на будь-якому проміжку , де , то функція розкладається в ряд Фур’є на . Коефіцієнти цього розкладу:

(10)

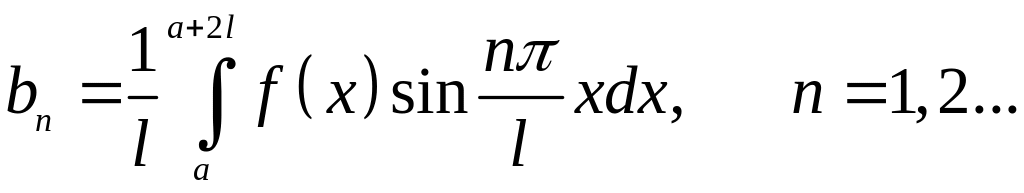
Фізичний зміст розкладу функції в тригонометричний ряд Фур’є

Гармонічне коливання задається функцією

,

де – амплітуда коливання, – частота, – початкова фаза. Йому відповідає пара членів тригонометричного ряду

,

де , .

Дійсно,

де , .

Гармонічна складова руху називається -ою гармонікою руху. Амплітуда -ої гармоніки .

У застосуваннях гармоніку записують в загальному вигляді

де – амплітуда, – частота.

Накладанням гармонік можна дістати різноманітні періодичні рухи на певному відрізку часу. Справедливе й обернене: користуючись розкладанням в ряд Фур’є, будь-яку функцію, що описує періодичний рух, можна розкласти на гармоніки.

Інтеграл та перетворення Фур’є

Нехай функція визначена на всій числовій осі і є абсолютно інтегрованою на ній, тобто

Тоді на довільному скінченному проміжку її можна розкласти в ряд Фур’є. Якщо вважати, що змінюється не від до , а перебігає всю числову вісь від до , то функція, зображена рядом Фур’є, вже не буде збігатися з зовні проміжка .

Для багатьох прикладних задач було б дуже корисно вивести з ряду Фур’є розклад, який зображав би функцію , визначену на . Таким розкладом є розклад в інтеграл Фур’є.

Інтеграл називається інтегралом Фур’є для функції .

Фур’є дістав його у 1811 році.

Перепишемо інтеграл в іншому вигляді, скориставшись формулою :

=

Позначимо:

; ;

Тоді:

Достатні умови зображення функції інтегралом Фур’є. Якщо функція визначена на проміжку і задовольняє умови:

1) є на ньому неперіодичною;

2) є на ньому абсолютно інтегрованою, тобто ;

3) на довільному скінченному відрізку функція задовольняє умови Діріхле, тобто є кусково-гладкою,

то її інтеграл Фур’є збігається в усіх точках відрізку .

Якщо – границя інтегралу Фур’є функції , то в усіх точках неперервності цієї функції , а в усіх точках розриву .

Інтеграл Фур’є для парних та непарних функцій

Нехай – парна функція, яка задовольняє умовам зображення функції інтегралом Фур’є. Враховуючи, що, , а також властивість інтегралів по симетричному відносно точки інтервалу від парних функцій, из рівностей (4) одержуємо:

Таким чином, інтеграл Фур’є парної функції запишеться так:

З аналогічних міркувань для непарної функції , одержимо

і, таким чином, інтеграл Фур’є непарної функції запишеться так:

,