Застосування лишків до обчислення інтегралів

Одним з найбільш важливих застосувань теорії аналітичних функцій є обчислення криволінійних, визначених та невластивих інтегралів за допомогою лишків. Основна теорема про лишки дозволяє звести обчислення інтегралів по замкнених контурах до обчислення лишків.

П риклад. Обчислити інтеграл .

Розв’язання.

1) Намалюємо контур інтегрування: коло з центром в точці і радіусом 4.

2) Знайдемо особливі точки функції .

, , , ,

З’ясуємо характер особливих точки:

, отже, – простий полюс функції .

, отже, – усувна особлива точка функції .

3) З’ясуємо, як розташовані особливі точки відносно контуру інтегрування.

Всередині контуру знаходяться обидві особливі точки підінтегральної функції, тому їх враховуємо при обчисленні інтегралу.

4) Обчислимо лишки в особливих точках. За формулою

.

Оскільки – усувна особлива точка, то .

5) За основною теоремою про лишки маємо:

.

Приклад. Обчислити інтеграл .

Розв’язання.

1 ) Намалюємо контур інтегрування–коло з центром в точці і радіусом 2.

2) Знайдемо особливі точки функції

:

, ,

З’ясуємо характер особливих точки:

, отже, , – прості полюси функції .

3) З’ясуємо, як розташовані особливі точки відносно контуру інтегрування.

Всередині контуру знаходяться дві особливі точки підінтегральної функції і , тому їх враховуємо при обчисленні інтегралу, всі інші особливі точки лежать поза контуром, тому при обчисленні інтегралу за основною теоремою про лишки їх не враховуємо.

4) Обчислимо лишки в особливих точках і . За формулою (9) обчислювати лишки в даному випадку незручно, тому скористаємося формулою (8)

,

5) Таким чином, за основною теоремою про лишки маємо:

.

Елементи операційного числення

Функцією-оригіналом називається будь-яка функція дійсного аргументу , що задовольняє умовам:

1) – інтегрована на будь-якому скінченому інтервалі осі (локально інтегрована).

2) Для всіх від’ємних функція : .

3) зростає при не швидше показникової функції, тобто, існують такі додатні сталі і , що для всіх виконується умова : .

Приклад 1. З’ясувати, чи є функція оригіналом ?

Розв’язання. Перевіримо виконання умов 1)–3).

1) Функція неперервана на будь-якому інтервалі , отже вона і інтегрована на будь-якому інтервалі .

2) Ця вимога виконана за умовою.

3) Для всіх має місце нерівність , отже і третя умова виконана.

Отже, функція – оригінал.

Найпростішою функцією-оригіналом є так звана функція Хевісайда:

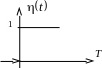
(Хевісайд Олівер (1850-1925) – англійський інженер і фізик, член Лондонського королівського товариства. Першим застосував операційне числення як один з методів прикладного аналізу, який дає можливість дуже просто розв’язувати складні задачі механіки, електротехніки тощо.)

Очевидно, що якщо деяка функція задовольняє умовам 1) та 3), то функція є оригіналом.

Наприклад, функція задовольняє умовам 1) та 3), тоді функція задовольняє умовам 1), 2) та 3) для всіх .

Зауваження. Для скорочення запису, ми у подальшому будемо у функції опускати множник . Наприклад, будемо писати , хоча будемо розуміти при цьому, що .

Означення. Зображенням Лапласа функції називається функція комплексної змінної , що визначається рівністю

Той факт, що є зображенням оригіналу символічно записують так , або ÷ .

Інтеграл з формули (1) часто називають інтегралом Лапласа або перетворенням Лапласа.

Приклад 1. Користуючись означенням, знайти зображення функції Хевісайда .

Розв’язання.

.

Отже,

÷

Теорема єдиності перетворення Лапласа. Перетворення Лапласа є єдиним в тому розумінні, що дві функції та , що мають одинакові зображення, збігаються в усіх точках неперервності (для будь-яких ).

Ця теорема має важливе прикладне значення. Якщо при розв’язуванні практичної задачі ми якимось чином визначили зображення шуканої функції, а потім по зображенню знайшли його оригінал, то на підставі цієї теореми ми робимо висновок, що знайдена функція є розв’язком поставленої задачі, і інших розв’язків не існує.