Модуль 4 Ряди. Елементи теорії функцій комплексної змінної Поняття числового ряду та його збіжності

Нехай – нескінченна послідовність дійсних чисел.

Вираз =

називається рядом (в даному випадку - числовим рядом), а елементи послідовності називаються членами ряду.

Звичайно член ряду описується як деяка функція від свого номера. Аналітичний вираз цієї функції називають загальним членом ряду.

.Сума перших членів ряду називається п-ю частинною суми ряду.

Означення. Ряд (1) називається збіжним, якщо послідовність його частинних сум має скінчену границю . Значення S цієї границі називається сумою ряду.

Якщо ж послідовність частинних сум скінченої границі не має, то ряд називається розбіжним (в цьому випадку ніякої суми йому не приписують).

Найпростіші властивості числових рядів

Розглянемо ряд = (1)

Ряд (2)

називається залишком ряду (1) після -го члена ( -м залишком).

Теорема 1. Ряд (1) збігається (розбігається) тоді і тільки тоді, коли збігається (розбігається) довільний його залишок.

Наслідок. Відкидання або приєднання до ряду скінченої кількості його членів не порушує його збіжність.

Теорема 2. Якщо всі члени збіжного ряду помножити на одне й те саме число , то збіжність його не буде порушена, а сума зміниться в разів.

Теорема 3. Збіжні ряди можна почленно додавати (віднімати). При цьому утворюється збіжний ряд, сума якого дорівнює сумі рядів-доданків.

,

.

Теорема 4. (необхідна умова збіжності ряду). Якщо ряд (1) збіжний, то

.

Теорема 5. (достатня умова розбіжності ряду). Якщо , то ряд розбіжний.

Приклад. 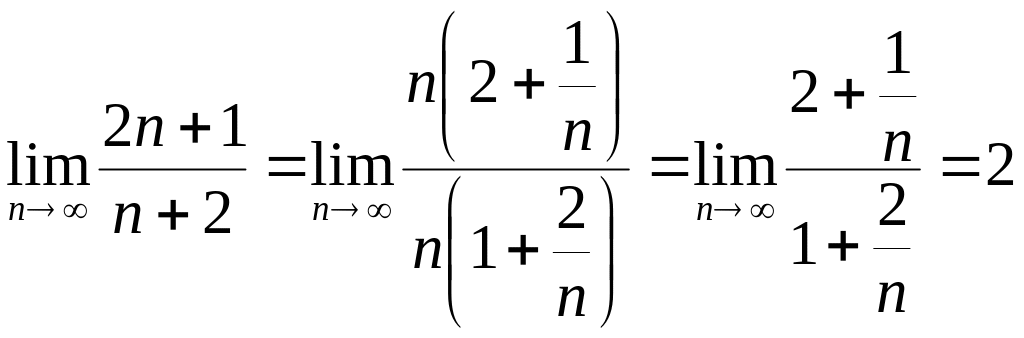– виконується достатня умова, тобто ряд розбіжний.

Достатні ознаки збіжності знакододатних числових рядів

Ряд, всі члени якого невід’ємні, називається знакододатним (або просто додатним):

, .

Властивості додатного числового ряду

1. Частинні суми знакододатного ряду утворюють монотонно неспадну послідовність

,

2. Ряд , збігається: , якщо послідовність його частинних обмежена зверху,тобто , причому мають місце нерівності .

П.1. Ознаки порівняння

Теорема (ознака порівняння). Нехай задано два додатних ряди

(1) і (2),

члени яких задовольняють умову . Тоді, якщо ряд (2) збігається, то збігається і ряд (1), а якщо ряд (1) розбігається, то розбігається і ряд (2).

Теорема (гранична ознака порівняння). Припустимо, що для рядів (1) і (2) існує границя . Тоді, якщо , то ряди (1) і (2) водночас збігаються або водночас розбігаються.

Зауваження. При дослідженні рядів за допомогою ознак порівняння за ряд (2) беруть ряд, поведінка якого відома. Найчастіше використовують геометричний ряд

і узагальнений гармонічний ряд (ряд Діріхле)

Приклад. Дослідити на збіжність ряди:

1. (1)

Підберемо ряд порівняння

Ряд (2) збігається як гармонічний ряд з показником

Оскільки , то за ознакою порівняння ряд (1) збігається.

2. (1)

Підберемо ряд порівняння

Ряд розбігається як гармонічний ряд.

З’ясуємо, чи поводить себе ряд (1), як ряд (2). За граничною ознакою порівняння

.

Оскільки , то ряди (1) і (2) водночас розбігаються.