3.7 Методы исследования нелинейных динамических систем и линеаризованных моделей.

Синтез нелинейной системы управления представляет собой решение задачи о выборе управления нелинейной системой в целях обеспечения устойчивости и заданных динамических свойств (времени регулирования, относительного коэффициента перерегулирования и времени срабатывания).

Для синтеза управления технической системой используют линеаризованную математическую модель.

Для выбора алгоритма управления:

Или передаточную функцию автоматического устройства

Для выбора коэффициента настройки автопилота используют метод расчета желаемой передаточной функции замкнутой системы при аналитическом решении, либо желаемой передаточной функции разомкнутой системы методом наращивания устойчивых контуров или другие подходы.

После синтеза алгоритма управления определяются области значений фазовых координат, на котором выполняются требования к заданным динамическим свойствам, к устойчивости и управляемости нелинейной системой.

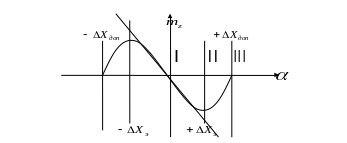
Комментарий: Первая область совпадения устойчивости и динамических характеристик нелинейной и линеаризованной модели определяют первый уровень пилотажных характеристик самолета. В этой области пилотирование самолета обеспечивается системными способами управления, самолет удобен в управлении.

Вторая область представляет собой область 2-ого уровня пилотажных характеристик. В этой области пилотирование самолета представляет определенные трудности, требует выдержки и специальных методов пилотирования. В ряде случаев эта область называется областью особых форм движения самолета и пилотажные характеристики самолета неудовлетворительны.

Третья область представляет собой область третьего уровня пилотажных характеристик. В этой области появляются критические и опасные формы движения, самолет не управляется обычными методами и движение самолета может привести к катастрофе.

При летных испытаниях самолета определяют области эксплуатационных значений параметров.

Область эксплуатационных значений параметров ограничивает область первого уровня пилотажных характеристик.

Область допустимых значений параметров ограничивает области второго уровня пилотажных характеристик.

Эти ограничения вводятся в алгоритм работы автопилота в виде фазовых координат и управления.

граничные условия

Система ограничений режима полета обеспечиваемая следующими проектными решениями:

1) Конструкция самолета в случае приближения к эксплуатационной и допустимой границам области полета создает тряску, вибрации и другие неблагоприятные формы поведения.

2) В автоматике используются блоки нелинейных ограничений, которые предусматривают уменьшение управляющих воздействий при выходе за ограничения.

3) Системы экспресс-контроля, запасы бортовой аппаратуры, регистрации параметров полета.

После синтеза автомата управления, с учетом блока нелинейного ограничения, выполняется математическое и натурное моделирование в полете переходных процессов при ступенчатой и импульсной даче рулей.