Министерство образования и науки российской федерации
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
Московский авиационный институт (национальный исследовательский университет)
«МАИ»
Факультет № 1: «Авиационная техника»
Кафедра № 106: «Динамика и управление летательных аппаратов»
Утверждено на заседании
Учебно-методического Совета факультета № 1
Протокол №
от «___»___________20 г.
Тексты лекций по дисциплине:
«Теория автоматического управления»
для основной образовательной программы
«Теория автоматического управления»
по направлению (специальности) подготовки
131402 «Динамика и управление полетом ЛА»
Разработано:
Маркин Н. Н.
Утверждено
на заседании кафедры
«___»____________ 20 г.
Москва – 2014 г.
Раздел 1. Линейный анализ технических систем
1.1 Введение
Любая техническая система описывается замкнутой структурной схемой. Элементами этой схемы являются:
Теория автоматического управления изучает решение следующих задач:
определение статических и динамических характеристик элементов системы управления;
исследование свойств элементов технической системы в частотной и временной области;
анализ структурных схем управления объектом и определение устойчивости, частотных и временных характеристик для разомкнутой и замкнутой системы;
синтез алгоритмов управляющих и корректирующих устройств для выполнения заданных технических требований;
исследование влияния нелинейных и дискретных элементов системы на режимы автоколебания и запасы устойчивости.
Для решения перечисленных задач в теории автоматического управления рассматриваются следующие разделы:
линейный анализ систем управления;
синтез линейных систем управления;
исследование динамики линейной системы с нелинейными и дискретными элементами в цепи обратной связи.
1.2 Линейный анализ системы управления
В данном разделе рассматриваются элементы систем управления, которые обладают следующими свойствами:
Статические характеристики линейных элементов описываются линейной зависимостью;
Динамика движения линейного элемента описывается линейными дифференциальными уравнениями;
Структура технической системы, которая включает объект управления, измерительные и управляющие устройства, включает только линейные элементы.
Статические
свойства:
,
но соотношение между ними будет
описываться некоторой статической
характеристикой:
,
где
– коэффициент усиления.
Динамические свойства:
Это дифференциальное
уравнение порядка
можно преобразовать к форме Коши:
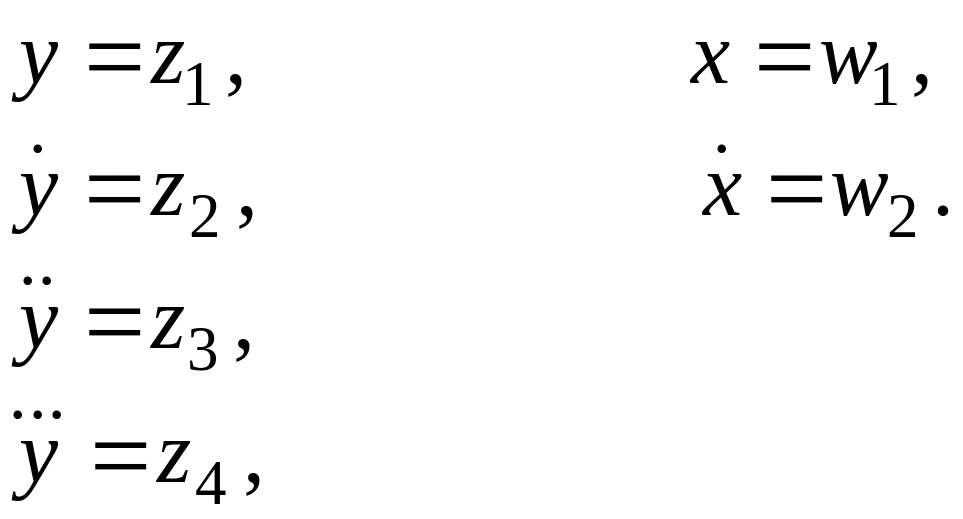
1.3 Исследование элементов линейной системы управления.
Для исследования линейных систем управления используются методы решения линейных дифференциальных уравнений, операторные и частотные методы.
Для исследования линейной системы необходимо составить дифференциальные уравнения на основе методов физики и теоретической механики и выполнить их преобразование операторными, частотными методами и найти решение дифференциальных уравнений.
Разработка математической модели:
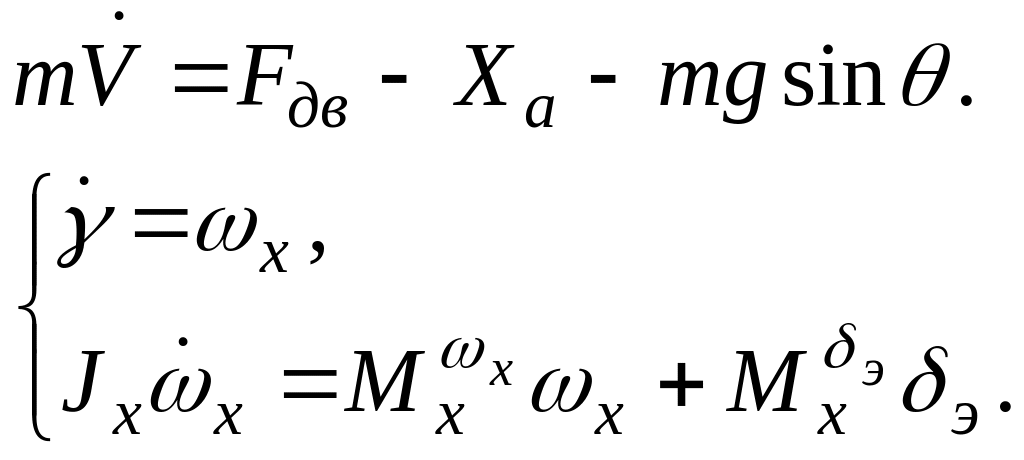
Уравнения разрешаются относительно входного и выходного сигналов в правой и левой части.
Преобразование:
Оператор Лапласа, операторная форма записи дифференциального уравнения и передаточная функция:
Лаплас ввел оператор
преобразования
.
Операторная форма записи дифференциального уравнения:
Передаточная функция представляет собой отношение изображения координаты на выходе к входной координате.
