
Принятие решений Методы анализа иерархий Томас Саати, Москва Радио и связь 1993 (Книга)
.pdf


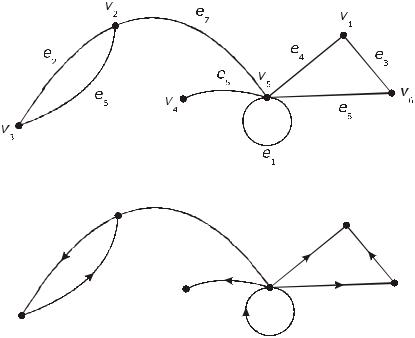

Рис. П.3
Два ребра с общей вершиной, или две вершины, являющиеся концевыми точками ребра, называют смежными. Вершина является изолированной, если она не ин-
цидентна никакому ребру. Обозначим граф следующим образом: G = (V , E ). Подграф графа G – это подмножество V1 множества вершин V и подмножество
E1 множества ребер E с теми же связями между вершинами и ребрами, что и в G .
Граф называют простым, если он не имеет ни петель, ни параллельных ребер, т. е. кратных ребер между парами вершин. В основном будем рассматривать простые графы, но поскольку в определение графов введены петли и параллельные ребра, при рассмотрении непростых графов будем вносить ясность.
С каждым ребром можно ассоциировать направления или ориентацию, указанную стрелкой. Тогда граф называют направленным (ориентированным) графом и его ребра называют дугами (см. рис. П.2). Направленный граф обозначают так:
D = (V , A).
Число ребер инцидентных вершине v V |
называют степенью вершины и обо- |
значают d (x). Обозначим d − (v) число дуг, |
направленных к v , а d + (v) – число |
дуг, направленных от v . При определении степени инцидентная вершине петля считается дважды. Для изолированной вершины имеем d (v) = 0 .
Обозначим число вершин и число ребер графа G = (V , E) через |
|
V |
|
и |
|
E |
|
|
|
соот- |
||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
ветственно, |
|
V |
|
называют степенью графа. Граф на рис. П.З имеет |
|
V |
|
= 7 и |
|
|
|
E |
|
=10 . |
||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
Граф называется конечным, если и |
|
V |
|
и |
|
E |
|
конечны, в противном случае – граф |
||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
бесконечный. |
Рассматривать будем только конечные графы. Степень |
|
v1 графа на |
|||||||||||||||||||||||||
рис. П.З равна 5: v7 – изолированная вершина.
Легко показать, что в любом графе число вершин нечетной степени четно. Для
этого отметим, что ∑d (v)= 2 E , так как каждое ребро считается дважды. Если
v V
обозначить через V0 и Ve множество вершин, имеющих нечётные и чётные степени соответственно, то получим этот результат, учитывая, что
246

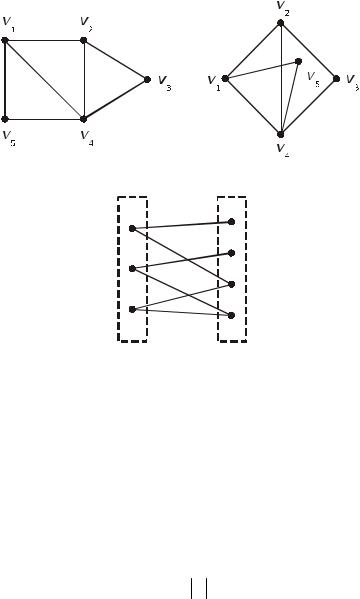
Рис. П.5
Рис. П.6
Специальный тип цикла в графе, важный для практических применений, назван в честь известного ирландского математика Уильяма Гамильтона (1805–1865). Мы называем цикл, который проходит через каждую вершину графа только однажды, гамильтоновым циклом. В то же время отметим, что имя швей царского математика Л. Эйлера (1707—1783) ассоциируется с эйлеровым графом, в котором ребра формируют цепь с каждым ребром графа, включенным в цепь только однажды. Цепь может быть разомкнута или может образовать цикл.
Два графа G = (V , E) и G′ = (V ′, E′) изоморфны друг другу, если существует
взаимно однозначное соответствие между V и V ′ и между E а E′, сохраняющее инцидентность. Например, два графа, показанные на рис. П.5, изоморфны.
Простой граф G = (V , E), у которого V = n и любая пара вершин соединена ребром, называется полным графом для n -вершин. Легко убедиться, что полный граф имеет n(n −1) 2 ребер. Так как любые два полных графа, имеющие одинако-
2 ребер. Так как любые два полных графа, имеющие одинако-
вое число вершин, изоморфны, говорят о полном графе для n -вершин.
Граф называется двудольным, если его вершины могут быть так разделены на два непересекающихся множества, что ребра графа будут только соединять вершины одного множества с вершинами другого (см. рис. П.6).
Обсуждение
Важным элементарным понятием, связанным с графом G на n вершинах, является связность. По сути, большая часть алгоритмической теории графов имеет отношение к связности, ее избыточности и даже ее отсутствию в графе.
Граф не связан (или несвязный), когда множество вершин V может быть разделено на два множества V1 и V2 так, что нет ребра, соединяющего вершину в V1 с вершиной в V2 , в противном случае говорят, что граф связный. Хотя две вершины
могут не быть прямо связанными ребром, оказывается возможно достижение одной из этих вершин из другой простой цепью. Если такая цепь, соединяющая любую пару вершин, имеется, то говорят, что граф связный. Иногда предпочитают примене-
248
