Сочетание энергетического и динамического подходов

Применим закон сохранения энергии. В состоянии I тело обладает потенциальной энергией

в состоянии II – кинетической

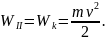
Поскольку , то

или

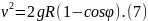
Нормальное ускорение можно выразить через линейную скорость как Тогда второй закон Ньютона в проекции на направление нормали для состояния II примет вид , или

Приравнивая выражения (7) и (8), , приходим к полученному ранее выражению Видно, что применение закона сохранения энергии целесообразнее решения уравнения (2).

Пример 22. Небольшой брусок начинает скользить по наклонной плоскости, составляющей угол α с горизонтом (рис.36). Коэффициент трения зависит от пройденного пути х по закону μ=kx, где k – постоянная. Найти путь, пройденный бруском до остановки.

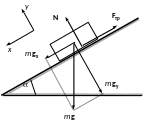
Рис.36

Решение.

Применение законов динамики

В данной задаче рассматривается движение под действием переменной результирующей силы.

На брусок действует Земля с силой тяжести mg и наклонная плоскость с силой нормального давления N и силой трения F_тр, величина которой равна

По второму закону Ньютона в векторной форме имеем:

Спроектируем это векторное уравнение на оси координат, указанные на рисунке,

Разрешая полученную систему уравнений относительно ускорения, получим зависимость ускорения от координаты х:

Далее решается кинематическая задача, связанная с преобразованием уравнений (задача третьего класса). Воспользуемся определениями скорости и ускорения

v = dx/dt, a = dv/dt,

и исключим переменные a и dt. В результате получим дифференциальное уравнение с разделяющимися переменными v и х:

Интегрируя это уравнение от момента, соответствующего началу движения (v₀=0, x₀=0) до остановки (v_ост=0, x=x_ост), получим

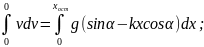
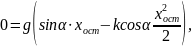
откуда искомая координата остановки равна

(корень x_ост=0 соответствует началу движения).

Энергетический способ

Значительно чаще эта задача решается с помощью закона изменения энергии.

Рис.37

В состоянии I (рис.37) тело обладает потенциальной энергией

в состоянии II (рис.37) - как кинетическая, так и потенциальная энергия равна нулю

Энергия изменяется вследствие работы, совершаемой силой трения:

величина силы трения, как отмечалось раньше, составляет

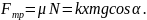
Как видно из формулы, сила трения зависит от пройденного расстояния (координаты х). При перемещении на расстояние dx совершается работа

Полная работа до остановки составит

Подставим полученные выражения в применяемый закон:

и выразим искомую величину - путь, пройденный телом до остановки,

Видно, что и в этом случае энергетический способ решения задачи оказывается более предпочтительным.

Решение задач различными способами.

В существующих учебных пособиях каждая задача решается, как правило, одним способом, что приводит к неверному представлению о существовании единственно возможного пути решения конкретной задачи. Убедимся, что это не так.

Пример 23. На сплошной однородный цилиндр симметрично намотаны две тонкие нерастяжимые и невесомые нити, свободные концы которых закреплены (рис.38). Под действием силы тяжести цилиндр, вращаясь, опускается вниз. Определить ускорение а_с, с которым перемещается центр масс этого цилиндра.

Рис.38

Решение. На цилиндр действуют сила тяжести mg, точкой приложения которой можно считать центр масс цилиндра, и две одинаковые по величине силы натяжения нити Т.

Применение законов динамики. Вариант 1

Рассмотрим движение цилиндра как наложение двух видов движения: перемещение цилиндра как целого с ускорением, равным ускорению центра масс и вращение вокруг оси, проходящей через центр масс (рис.39). Поэтому применяются два закона динамики, каждый из которых описывает соответствующий вид движения.

Рис.39

Первый вид движения подчиняется уравнению движения центра масс:

второй - уравнению динамики вращательного движения:

Момент инерции цилиндра относительно оси, проходящей через центр масс составляет , моменты M_mg=0, M_2T=2TR. С учетом этих соотношений уравнение (2) принимает вид

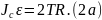
Уравнение кинематической связи, как и при решении других подобных ранее рассмотренных задач, имеет вид

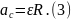
Разрешим систему уравнений (1) - (3) относительно искомой величины. Выразим из (3) угловое ускорение и подставим в формулу (2):

Полученную из последнего выражения силу натяжения нити подставим в (1) откуда и получим искомое ускорение

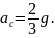
Применение законов динамики. Вариант 2

Движение цилиндра можно рассматривать как чисто вращательное относительно мгновенной оси О с угловым ускорением ε (рис.40).

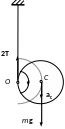
Рис.40

Уравнение динамики вращательного движения в данном случае имеет вид

в котором момент инерции относительно оси вращения находится по теореме Штейнера Подстановка выражения дает

Моменты сил относительно оси О также имеют иной вид, отличающийся от предыдущего случая: M_mg=mgR, M_2T=0. Ускорение центра масс а_с является тангенциальным при движении точки С по окружности радиуса R, следовательно Подстановка полученных выражений в уравнение (1) приводит к тому же выражению искомого ускорения

Применение законов динамики во второй формулировке

Как в предыдущем случае, будем рассматривать движение цилиндра как чисто вращательное относительно мгновенной оси О (рис.41).

Рис.41

Уравнение динамики вращательного движения можно представить в ином виде, а именно, скорость изменения момента импульса равна сумме моментов сил, действующих на тело:

Момент импульса цилиндра относительно оси О , моменты сил M_mg=mgR, M_2T=0, поэтому

Учитывая определение углового ускорения 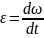и формулу связи 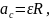приходим к выражению для ускорения цилиндра

Безусловно, законы динамики во второй формулировке можно применять и при интерпретации движения цилиндра как сочетания поступательного и вращательного.

Применение закона сохранения энергии. Вариант 1

Закон сохранения энергии, как и законы динамики, можно применять по разному, в зависимость от описания движения цилиндра.

Рассмотрим первый способ, при котором движение цилиндра рассматривается как сложное. Пусть центр масс за время t опустился на расстояние h. В начальном состоянии цилиндр обладал потенциальной энергией , спустя время t - кинетической, , причем . Угловая скорость вращения относительно оси, проходящей через центр масс связана с линейной скоростью центра масс соотношением Тогда

Подставим полученные выражения в закон сохранения энергии

Учтем, что при движении с постоянным ускорением Тогда последнее выражение принимает вид из которого легко получить ускорение цилиндра

Применение закона сохранения энергии. Вариант 2

Рассмотрим вращение цилиндра относительно мгновенной оси с угловой скоростью ω. Скорость центра масс связана с угловой скоростью соотношением . В данном случае выражение кинетической энергии принимает вид 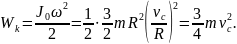По закону сохранения энергии 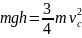с учетом соотношений получается прежний ответ.

Применение закона изменения момента импульса

Рассмотрим движение цилиндра как чисто вращательное относительно мгновенной оси О. Закон изменения момента импульса имеет вид

В начальном состоянии момент импульса цилиндра L_I=0, спустя время t после начала движения , моменты внешних сил M_mg=mgR, M_2T=0; поэтому

или

Учитывая, что , и определение ускорения 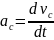, находим ускорение цилиндра

Применение законов изменения импульса и момента импульса

Если описывать сложное движение цилиндра, то, кроме закона изменения момента импульса, необходимо применить и закон изменения импульса.

В начальном состоянии момент импульса цилиндра относительно оси, проходящей через центр масс L_I=0, спустя время t после начала движения 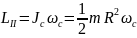, моменты внешних сил M_mg=0, M_2T=2TR; поэтому

Закон изменения импульса примет вид

Исключая из системы уравнений силу натяжения нити Т и учитывая, что , приходим к выражению

Здесь представлено семь способов решения задачи. Это не означает, что любую задачу можно решить множеством способов. Иногда существует один единственно возможный путь решения, например в том случае, когда недостаточно сведений о характере взаимодействия тел в системе. В частности, это относится к описанию процессов взрыва или удара. Тем не менее, иметь представление о существующих возможностях весьма полезно.

Применение неинерциальной системы отсчета.

Пример 24. Плоскую спираль из жесткой гладкой проволоки, расположенную в горизонтальной плоскости, вращают с постоянной угловой скоростью ω вокруг неподвижной вертикальной оси О (рис.42). По спирали без трения скользит небольшая муфта массой m. Найти ее скорость относительно спирали v’ как функцию расстояния r от оси вращения, если муфта начала двигаться от этой оси со скоростью .

Рис.42

Решение. В условии задачи как известная величина ( ), так и искомая (v’) заданы в системе отсчета, связанной со спиралью. На муфту действуют реальные силы тяжести mg и реакции со стороны спирали N. Силой трения пренебрегаем, так как проволока гладкая. Поскольку муфта движется относительно вращающейся системы отсчета, в перечень сил следует включить как центробежную силу F_цб, так и кориолисову силу инерции F_кор. Выражения для сил инерции имеют вид

Центробежная сила направлена от оси вращения, кориолисова сила согласно правилу векторного произведения направлена перпендикулярно векторам 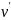и ω (рис.43).

Рис.43

Сила тяжести, сила реакции спирали и кориолисова сила работы не совершают, так как они перпендикулярны к направлению перемещения. Поэтому изменение кинетической энергии муфты происходит только за счет работы центробежной силы

Выражения для кинетической энергии в состояниях, о которых говорится в условии задачи, имеют вид

Получим выражение для работы центробежной силы. При перемещении на расстояние ds совершается элементарная работа , где α - угол между векторами силы и перемещения. Проекция вектора перемещения на направление вектора силы равна dr=dscosα. Поэтому с учетом выражения для центробежной силы получаем элементарную работу После интегрирования находим выражение для полной работы

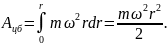
Подставляя выражения для кинетической энергии и работы в формулу (1)

находим скорость муфты относительно спирали как функцию расстояния от оси вращения: