
- •Лекция 7. Приложение общих теорем к динамике твердого тела.
- •Силы инерции при поступательном движении.
- •Принцип Даламбера.
- •Главный вектор и главный момент сил инерции твёрдого тела.
- •Движение тела с переменной массой.
- •Сочетание энергетического и динамического подходов
- •Решение нестандартных задач.
- •Задачи для самостоятельного решения
Главный вектор и главный момент сил инерции твёрдого тела.
Система
сил инерции твёрдого тела можно заменить
одной силой, равной
и приложенной в центре О,
и парой с моментом, равным
.
Главный вектор системы сил, как известно,
не зависит от центра приведения и может
быть вычислен заранее. Т.к.
 ,
то
,
то

Следовательно, главный вектор сил инерции тела, совершающего любое движение, равен произведению массы тела на ускорение его центра масс и направлен противоположно этому ускорению.
Прикладывается главный вектор к точке приведения, которую можно назначить в любом месте, т.е. он не зависит от выбора этой точки.
Если
ускорение
 разложить на касательное и нормальное,
то вектор
разложиться на составляющие
разложить на касательное и нормальное,
то вектор
разложиться на составляющие

С определением главного момента сил инерции возникает немало сложностей. Рассмотрим несколько частных случаев.
1.
Поступательное движение.
В этом случае тело никакого вращения
вокруг центра масс С
не имеет. Отсюда заключаем, что
 ,
и равенство (1) даёт
,
и равенство (1) даёт
 .
.
Следовательно, при поступательном движении силы инерции твёрдого тела приводят к одной равнодействующей, равной и проходящей через центр масс тела.
2. Плоскопараллельное движение. Пусть тело имеет плоскость симметрии и движется параллельно ей. Вследствие симметрии главный вектор и результирующая пара сил инерции, так же как и центр масс С тела, лежат в плоскости симметрии.
Тогда,
помещая центр приведения в точке С,
получим из равенства (16)
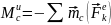 .
С другой стороны
.
С другой стороны
 .
Отсюда заключаем, что
.
Отсюда заключаем, что


Рис.7
Таким
образом, в рассмотренном случае движение
системы сил инерции приводится к
результирующей силе, равной
[формула (18)] и приложенной в центре масс
С
тела (рис.7), и к лежащей в плоскости
симметрии тела паре, момент которой
определяется формулой (18). Знак минус в
формуле показывает, что направление
момента
 противоположно направлению углового
ускорения тела.
противоположно направлению углового
ускорения тела.
3.
Вращение вокруг
оси, проходящей через центр масс тела.
Пусть опять тело имеет плоскость
симметрии, а ось вращения СZ
перпендикулярна к этой плоскости и
проходит через центр масс тела. Тогда
данный случай будет частным случаем
предыдущего. Но при этом
 а следовательно, и
а следовательно, и
 .
.
Таким образом, в рассмотренном случае система сил инерции приводится к данной паре, лежащей в плоскости, перпендикулярной к оси вращения тела, и имеющей момент
 .
.
При решение задач по формулам (16) и (18) вычисляются модули соответствующих величин, а направление их указывают на чертеже.
Приложение общих теорем к динамике твердого тела.
Вращательное движение твёрдого тела.
Рассмотрим приложения общих теорем динамики к некоторым задачам о движении абсолютно твёрдого тела. Так как изучение поступательного движения твёрдого тела сводится к задачам динамики точки, то мы начнём непосредственно с рассмотрения вращательного движения.

Рис.8
Пусть
на твёрдое тело, имеющее неподвижную
ось вращения Z
(рис.8), действует система заданных сил
 .
Одновременно на тело действуют реакции
подшипников
.
Одновременно на тело действуют реакции
подшипников
 и
и
 .
Чтобы исключить из уравнения движения
эти наперед неизвестные силы, воспользуемся
теоремой моментов относительно оси
Z. Так как
моменты сил
и
относительно оси Z
равны нулю, то получим:
.
Чтобы исключить из уравнения движения
эти наперед неизвестные силы, воспользуемся
теоремой моментов относительно оси
Z. Так как
моменты сил
и
относительно оси Z
равны нулю, то получим:
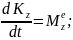

Будем
в дальнейшем величину
 называть вращающим моментом.
называть вращающим моментом.
Подставляя
в предыдущее равенство значение
 ,
найдём:
,
найдём:

Уравнение представляет собой дифференциальное уравнение вращательного движения твёрдого тела. Из него следует, что произведение момента инерции тела относительно оси вращения на угловое ускорение равно вращающему моменту:

Равенство показывает, что при данном чем больше момент инерции тела, тем меньше угловое ускорение и наоборот. Следовательно, момент инерции тела действительно играет при вращательном движении такую же роль, как масса при поступательном, т.е. является мерой инертности тела при вращательном движении.
Отметим следующие частные случаи:
1)
Если
 ,
то
,
то
 ,
т.е. тело вращается равномерно.
,
т.е. тело вращается равномерно.
2)
Если
 ,
то и
,
то и
 ,
т.е. тело вращается равнопеременно.
,
т.е. тело вращается равнопеременно.
Пример 3. Стержень весом Р и длиной l качается как маятник в вертикальной плоскости, вращаясь вокруг горизонтальной оси О (рис.9).

Рис.9
Решение. Составим уравнение качаний стержня.
Так
как
 и реакции оси не учитываются, то получим
и реакции оси не учитываются, то получим

Физический маятник
Физическим маятником называется твёрдое тело, которое может совершать колебания вокруг неподвижной горизонтальной оси под действием силы тяжести.

а) б)
Рис.10
Изобразим сечение маятника плоскостью, перпендикулярной оси подвеса и проходящей через центр масс маятника С (рис.10, а).
Введём
обозначения: Р
– вес маятника,
а – расстояние
ОС
от центра масс до оси подвеса, I0
– момент инерции маятника относительно
оси подвеса. Положения маятника будет
определять угол
 отклонение линии ОС
от вертикали.
отклонение линии ОС
от вертикали.
Для
определения закона колебаний маятника
воспользуемся дифференциальным
уравнением вращательного движения. В
данном случае
 (знак минус взят потому, что при
(знак минус взят потому, что при
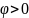 момент отрицателен, а при
момент отрицателен, а при
 – положителен) и уравнение принимает
вид:
– положителен) и уравнение принимает
вид:
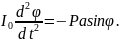
Деля обе части равенства на I0 и вводя обозначение

найдём дифференциальное уравнение колебаний маятника в виде
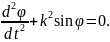
Полученное
дифференциальное уравнение в обычных
функциях не интегрируется. Ограничимся
рассмотрением малых колебаний маятника,
считая приближенно
 (это можно сделать, когда угол
меньше одного радиана). Тогда будем
иметь
(это можно сделать, когда угол
меньше одного радиана). Тогда будем
иметь

Это дифференциальное уравнение совпадает по виду с дифференциальным уравнением свободных прямолинейных колебаний точки, и его общее решение по аналогии имеет вид:
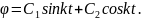
Полагая,
что начальный момент t = 0 маятник отклонён
на малый угол
 и отпущен без начальной скорости (
и отпущен без начальной скорости (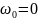 ),
найдём для постоянных интегрирования
значения: С1
= 0, С2
=
),
найдём для постоянных интегрирования
значения: С1
= 0, С2
= .
Тогда закон малых колебаний маятника
при данных начальных условиях будет:
.
Тогда закон малых колебаний маятника
при данных начальных условиях будет:

Следовательно, малые колебания физического маятника являются гармоническими. Период малых колебаний физического маятника, если заменить k его значением, определяется формулой:

Полученные результаты охватывают и случай так называемого математического маятника, т.е. груза малых размеров (которые будем рассматривать как материальную точку), подвешенного на нерастяжимой нити длиной l, массой которой, по сравнению с массой груза, можно пренебречь (рис.57, б). Для математического маятника, т.к. он представляет собой систему, состоящую из одной материальной точки, очевидно, будет
 .
.
Подставляя
эти величины в равенство ,
найдем, что период малых колебаний
математического маятника определяется
формулой
,
найдем, что период малых колебаний
математического маятника определяется
формулой

Из
сравнения формул
и
 видно, что при длине
видно, что при длине

период колебаний математического маятника совпадает с периодом колебаний соответствующего физического маятника.
Длина
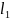 такого математического маятника, период
колебания которого равен периоду
колебаний данного физического маятника,
называется приведенной длиной физического
маятника. Точка K,
отстоящая от оси подвеса на расстоянии
такого математического маятника, период
колебания которого равен периоду
колебаний данного физического маятника,
называется приведенной длиной физического
маятника. Точка K,
отстоящая от оси подвеса на расстоянии
 ,
называется центром качания физического
маятника (рис.57).
,
называется центром качания физического
маятника (рис.57).
Замечая,
что по теореме Гюйгенса
 ,
мы можем привести формулу к виду
,
мы можем привести формулу к виду
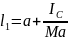
Отсюда следует, что расстояние OK всегда больше чем OC = a, т.е. что центр качаний физического маятника всегда расположен ниже его центра масс.
Плоскопараллельное движение твердого тела.
Положение тела, совершающего, плоскопараллельное движение, определяется в любой момент времени положением полюса и углом поворота тела вокруг полюса. Задачи динамики будут решаться проще всего, если за полюс взять центр масс С тела (рис.11) и определять положение тела координатами XC, YC и углом .

Рис.11
На
рис.5 изображено сечение тела плоскостью,
параллельной плоскости движения и
проходящей через центр масс С.
Пусть на тело действуют внешние силы
,
лежащие в плоскости этого сечения. Тогда
уравнения движения точки С
найдём по
теореме о движении центра масс

 ,
,
а вращательное движение вокруг центра С будет определятся уравнением
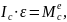
т.к. теорема, из которой получено это уравнение, справедливо и для движения системы вокруг центра масс. В результате, проектируя обе части равенства на координатные оси, получим:


Эти уравнения представляют собой дифференциальные уравнения плоскопараллельного движения твёрдого тела. С их помощью можно по заданным силам определить закон движения тела или, зная закон движения тела, найти главный вектор и главный момент действующих сил.
При несвободном движении, когда траектория центра масс известна, уравнения движения точки С удобно составлять в проекциях на касательную τ и главную нормаль n к этой траектории. Тогда получим:
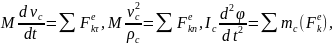
где
 - радиус кривизны траектории центра
масс.
- радиус кривизны траектории центра
масс.
Пример 4. Однородный круглый цилиндр скатывается по наклонной плоскости (рис.12). Цилиндр совершает плоскопараллельное движение.

Рис.12
Решение.
Так как
 и, значит,
и, значит,
 составим дифференциальное уравнение
вращения относительно оси
составим дифференциальное уравнение
вращения относительно оси
 проходящей через мгновенный центр
скоростей.
проходящей через мгновенный центр
скоростей.
Момент
инерции цилиндра относительно оси
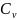

Поэтому уравнение получится таким

Знак (–) указывает на направление углового ускорения – по часовой стрелке.
Обратим внимание на то, что реакции не вошли в уравнение.
Чтобы определить реакцию Fтр, составим еще одно дифференциальное уравнение вращения, относительно центральной оси С :

Отсюда

Конечно,
 .
Чтобы тело катилось без скольжения
должно выполняться условие
.
Чтобы тело катилось без скольжения
должно выполняться условие
 или
или
 .
Поэтому коэффициент трения скольжения
должен удовлетворять условию
.
Поэтому коэффициент трения скольжения
должен удовлетворять условию
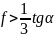 .
.
Пример 5. Балочка АВ длиной l и весом Р падает, скользя концами по гладким поверхностям стены и пола (рис.13). Составим дифференциальное уравнение вращения.

Рис.13
Решение.
Здесь
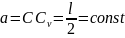 .
Поэтому опять выгоднее составить
дифференциальное уравнение вращения
относительно оси
.
Тем более, что неизвестные реакции
.
Поэтому опять выгоднее составить
дифференциальное уравнение вращения
относительно оси
.
Тем более, что неизвестные реакции
 и
и
 не войдут в это уравнение.
не войдут в это уравнение.
Так
как
 то уравнение получится таким:
то уравнение получится таким:
 .
.
Отсюда

Пример
6. Тело, имеющее
форму половины кругового цилиндра,
катается по горизонтальной плоскости
без скольжения (рис.14). Вес его – Р.
Положение центра тяжести определяется
расстоянием
 ,
момент инерции относительно оси О:
I0=0,5Mr2
,
момент инерции относительно оси О:
I0=0,5Mr2

Рис.14
Решение. Поскольку неизвестны ни сила трения Fтр, ни нормальная реакция N, конечно следует составлять дифференциальное уравнение вращения относительно оси .
Момент
инерции тела относительно оси
по теореме Гюйгенса-Штейнера,
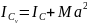 ,
а I0=IC+Me2,
поэтому
,
а I0=IC+Me2,
поэтому
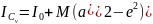 .
.


Количество
движения
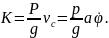
Составляем дифференциальное уравнение:


После подстановки значения a, получим

и,
окончательно, подставив значение
 ,
,

Пример
7. Стержень
качался как маятник, вращаясь в
вертикальной плоскости вокруг шарнира
О
(рис.15). В момент, когда стержень был в
вертикальном положении и угловая
скорость его была
 ,
шарнир разрушился. Определим дальнейшее
движение стержня.
,
шарнир разрушился. Определим дальнейшее
движение стержня.
Решение. Стержень начнет совершать плоскопараллельное движение. На рис.62 показано его промежуточное положение.

Рис.15
Составим дифференциальные уравнения движения.

Интегрируем их дважды:

Начальные условия: при t = 0

Подставив
их в последние шесть уравнений, получим
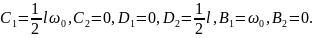
Тогда уравнения плоскопараллельного движения стержня
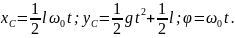
Например,
стержень займет горизонтальное положение,
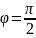 ,
в момент
,
в момент
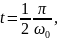 когда центр масс его будет в точке с
координатами
когда центр масс его будет в точке с
координатами

Сложное движение твердого тела и системы тел.
Пример 8. На гладкое проволочное кольцо радиуса R надет маленький шарик. Кольцо вместе с шариком вращается вокруг вертикальной оси, проходящей через диаметр кольца, с угловой скоростью ω. Где находится шарик?
Решение. Решение этой задачи можно осуществить, применяя разные системы отсчета - как инерциальную (ИСО), связанную с Землей, так и неинерциальную (НИСО), связанную с кольцом; различным может быть и выбор осей координат. Чтобы показать, что в любом случае состав операций, приведенный в алгоритмическом предписании, не зависит от выбора системы отсчета, будем указывать их номера.
Решение задачи в ИСО
1. Рассмотрим решение этой задачи в инерциальной системе отсчета, связанной с Землей (рис.16).

Рис.16
2. Шарик можно рассматривать как материальную точку, которая вращается вместе с кольцом с угловой скоростью ω.
3. На шарик действуют две силы: сила тяжести со стороны Земли mg и реакция кольца N. Поскольку по условию задачи кольцо гладкое, силой трения можно пренебречь.
4. Второй закон Ньютона в векторной форме имеет вид

5. Шарик движется по окружности радиуса r=R∙sinα с постоянной угловой скоростью ω. Его ускорение равно
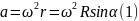
и направлено к центру окружности C. Совместим с вектором ускорения ось х, ось у направим вертикально вверх, как показано на рисунке.
6. Запишем второй закон Ньютона в проекциях на оси координат:
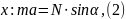
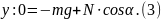
7. Из
(3) находим
 Подставляя это выражение и формулу (1)
в уравнение (2), получаем
Подставляя это выражение и формулу (1)
в уравнение (2), получаем


Из полученного уравнения находим следующие условия равновесия:
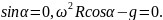
Это
означает, что при вращении с малой
угловой скоростью
 шарик подниматься не будет, равновесие
соответствует значению
шарик подниматься не будет, равновесие
соответствует значению
 .
При вращении с большой
угловой скоростью
.
При вращении с большой
угловой скоростью
 ,
что эквивалентно условию cosα<1,
равновесное положение соответствует
углу
,
что эквивалентно условию cosα<1,
равновесное положение соответствует
углу

Решение задачи в НИСО
1. Рассмотрим решение этой же задачи в неинерциальной системе отсчета, вращающейся с угловой скоростью ω (рис.17). В этой системе отсчета шарик покоится.
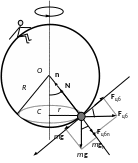
Рис.17
2.
Кроме реальных сил взаимодействия,
действующих на шарик - силы тяжести mg
и нормального давления
 ,
следует ввести центробежную силу инерции
Fцб,
величина которой равна
,
следует ввести центробежную силу инерции
Fцб,
величина которой равна
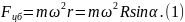
Шарик не движется относительно кольца, следовательно, его ускорение равно нулю.
3. Второй закон Ньютона превращается в условие равновесия шарика в системе отсчета, связанной с кольцом:

4. Спроектируем векторное уравнение на тангенциальное τ (касательное к окружности) и нормальное n (перпендикулярное касательной) направления.

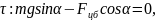
или с учетом (1)


Из уравнения (3) получим те же условия равновесия, что и ранее:

откуда

Пример 9. Внутри конуса, установленного в ракете, поднимающейся вертикально вверх с ускорением а0, находится небольшое тело (рис.18). Конус имеет при вершине угол 2α и вращается вокруг своей оси с угловой скоростью ω. На каком максимальном расстоянии l от вершины конуса будет находиться тело, если коэффициент трения между телом и поверхностью конуса равен μ? Ось конуса совпадает с продольной осью ракеты.

Рис.18
Решение.
1. Система отсчета (наблюдатель находится на конусе) - неинерциальная. Относительно наблюдателя на Земле она движется вверх с ускорением а0 и вращается с угловой скоростью ω.
2. Тело (материальная точка) неподвижна относительно конуса, вместе с конусом вращается, а вместе с ракетой движется равноускоренно с ускорением а0.
3. На тело кроме реальных сил взаимодействия - силы тяжести mg, нормального давления N и силы трения Fтр,

следует ввести центробежную силу инерции Fцб, величина которой равна
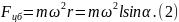
и силу инерции, связанную с поступательным прямолинейным движением системы отсчета: Fин = - mа0. Модуль этой силы равен

Тело в выбранной системе отсчета неподвижно, его ускорение равно нулю.
4. Второй закон Ньютона превращается в условие равновесия:

5. Далее решение задачи очевидно: проектировать векторное уравнение на оси координат и разрешать полученную систему алгебраических уравнений. Оси координат указаны на рисунке.
6. Второй закон Ньютона в проекциях на оси координат имеет вид


7. Подставляя в уравнения (4) - (5) выражения (1) - (3), разрешаем систему относительно радиуса окружности

Следовательно, расстояние от вершины конуса до тела равно

Пример
10. На
горизонтальной шероховатой поверхности
лежит катушка ниток массы m.
Ее момент инерции относительно собственной
оси
 ,
где β
- числовой коэффициент, R
- внешний
радиус катушки. Радиус намотанного слоя
ниток равен
r. Катушку без
скольжения начали тянуть за нить с
помощью постоянной силы F, направленной
под углом α
к горизонту. Найти модуль и направление
ускорения оси катушки.
,
где β
- числовой коэффициент, R
- внешний
радиус катушки. Радиус намотанного слоя
ниток равен
r. Катушку без
скольжения начали тянуть за нить с
помощью постоянной силы F, направленной
под углом α
к горизонту. Найти модуль и направление
ускорения оси катушки.
Решение. Рассмотрим два варианта решения этой задачи. Во-первых, движение катушки можно считать наложением двух видов движения: поступательного со скоростью центра масс и вращения вокруг оси симметрии. Соответственно, записываются два динамических закона: уравнение движения центра масс и уравнение динамики вращательного движения. Во-вторых, движение катушки можно представить как чисто вращательное движение вокруг мгновенной оси О, проходящей через точки касания катушки о горизонтальную поверхность. В этом случае достаточно одного динамического уравнения - уравнения вращательного движения.
Обратимся к первому варианту решения задачи. Движение катушки можно считать наложением двух видов движения: поступательного со скоростью центра масс и вращения вокруг оси симметрии.
Выбираем инерциальную систему отсчета, связанную с Землей.

Рис.19
На катушку действуют Земля с силой тяжести mg, нить с силой F и горизонтальная поверхность с силами нормального давления N и трения Fтр.
Поскольку
катушка движется без проскальзывания,
то

Рассмотрим поступательное движение. Уравнение движения центра масс в векторной форме имеет вид
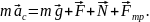
Оси координат указаны на рис.19. Спроектируем векторное уравнение на оси координат:


Рассмотрим вращательное движение. Уравнение динамики вращательного движения катушки относительно ее оси в векторной форме имеет вид

Моменты
сил F
и Fтр
направлены вдоль оси вращения, но в
противоположные стороны. Поэтому
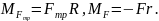 Учитывая, что Mmg=0,
MN=0,
J=mR2,
запишем уравнение динамики вращательного
движения в проекции на ось z,
направленную вдоль оси вращения “от
нас”:
Учитывая, что Mmg=0,
MN=0,
J=mR2,
запишем уравнение динамики вращательного
движения в проекции на ось z,
направленную вдоль оси вращения “от
нас”:

Составим уравнение, связывающее кинематические величины, входящие в уравнения (1) и (3), ac и ε. Для этого изобразим катушку в двух состояниях.
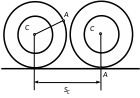
Рис.20
Из рис.20 видно, что перемещение центра катушки sc при отсутствии проскальзывания равно длине дуги, на которую опирается угол поворота катушки φ вокруг оси С. Следовательно,

Продифференцируем это выражение дважды по времени

Учитывая определения линейного и углового ускорений

получим уравнение кинематической связи:

Систему уравнений (1) - (4) нетрудно разрешить относительно искомой величины:

Анализ
полученного выражения приводит к
заключению, что при
 ускорение оси катушки ac>0
и катушка движется в направлении оси
х.
При
ускорение оси катушки ac>0
и катушка движется в направлении оси
х.
При
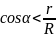 ускорение ac<0
и катушка движется в противоположном
направлении. При
ускорение ac<0
и катушка движется в противоположном
направлении. При
 катушка покоится ac=0.
катушка покоится ac=0.
Рассмотрим второй вариант решения задачи - катушка вращается вокруг мгновенной оси О (рис.21).

Рис.21
Относительно этой оси моменты силы тяжести mg, силы нормального давления N и силы трения Fтр равны нулю, так как линии действия этих сил проходят через мгновенную ось. Уравнение динамики вращательного движения примет вид

где J0 - момент инерции относительно оси О. По теореме Штейнера

Плечо d силы F находим геометрически. Из треугольника ACD выразим гипотенузу CD через прилежащий катет AC = r:

Затем
находим
 а из треугольника OBD
а из треугольника OBD
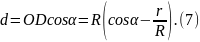
Подставляя (6) и (7) в (5), получаем
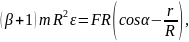
откуда выражаем угловое ускорение

Ускорение
центра масс катушки ac
является тангенциальным ускорением
точки С
при вращении вокруг оси О,
оно связано с угловым ускорением ε
соотношением:
 .
Следовательно, мы получаем прежнее
выражение для ускорения центра масс
.
Следовательно, мы получаем прежнее
выражение для ускорения центра масс
Данный
способ описания облегчает анализ
направления движения. Действительно,
если линия действия силы проходит выше
мгновенной оси О
 ,
то момент силы F
вызывает
вращение по
часовой стрелке,
катушка движется вправо
(рис.22).
,
то момент силы F
вызывает
вращение по
часовой стрелке,
катушка движется вправо
(рис.22).

Рис.22
Если
же линия действия силы проходит ниже
оси О
 ,
момент силы F
вызывает вращение против
часовой стрелки,
катушка движется влево.
,
момент силы F
вызывает вращение против
часовой стрелки,
катушка движется влево.
Если
линия действия силы F
проходит через
мгновенную ось
О, катушка
неподвижна,
т.к. момент силы равен нулю. Из рисунка
видно, что равновесию соответствует
угол α,
удовлетворяющий условию
 что согласуется с ранее полученным
результатом.
что согласуется с ранее полученным
результатом.
Пример 11. В установке известны массы тел m1 и m2, коэффициент трения μ между телом m1 и горизонтальной плоскостью, а также масса блока m, который можно считать однородным диском (рис.23). Скольжения нити по блоку нет. В момент t = 0 тело m2 начинает опускаться. Пренебрегая массой нити и трением в оси блока, найти ускорения всех тел.

Рис.23
Решение. В системе тел, изображенной на рис.23, бруски движутся поступательно и их движение описывается вторым законом Ньютона:


Спроектируем эти уравнения на оси координат:



Блок массивный, поэтому для описания его вращения запишем основное уравнение динамики вращательного движения:

Учитывая,
что момент инерции сплошного однородного
диска равен
 ,
а модули моментов сил, действующих на
блок,
,
а модули моментов сил, действующих на
блок,

спроектируем последнее векторное уравнение на ось z, направленную перпендикулярно плоскости рисунка “от нас” (направление оси соответствует направлению вектора углового ускорения):

Чтобы система уравнений была полной, в нее следует включить уравнения кинематической связи. Для ее записи изобразим систему тел в двух состояниях (рис.24) и найдем соотношение между перемещениями обоих грузов и углом поворота блока. Из условия нерастяжимости нити следует, что AA’=BB’=CC’, или


Рис.24
Дифференцируя это выражение дважды по времени, получаем уравнение связи между ускорениями:
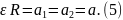
Систему
(1)-(5) с учетом соотношения
 нужно разрешить относительно ε
и a.
Из уравнения (2) N=m1g,
следовательно,
нужно разрешить относительно ε
и a.
Из уравнения (2) N=m1g,
следовательно,
 .
Тогда уравнение (1) перепишется в виде
.
Тогда уравнение (1) перепишется в виде

Подставляя
T1
из (6), T2
из (3) и
 из (5) в уравнение (4), получаем
из (5) в уравнение (4), получаем
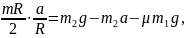
откуда

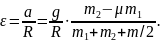
Эта задача позволяет сделать вывод о натяжении нитей в приближении невесомого блока. Положив в формуле (4) m= 0, получаем: T1=T2, т.е. натяжение вдоль невесомой нити одинаково по обе стороны блока. Это условие постулировалось при решении ряда задач в школьном курсе физики.
Пример 12. Наклонная доска, составляющая с горизонтом угол 60°, приставлена к горизонтальному столу (рис.25). Два груза массой по 1 кг каждый соединены легкой нитью, перекинутой через невесомый блок, и могут перемещаться соответственно по доске и столу. Найти силу натяжения нити a и ускорение системы T, если коэффициент трения тел о поверхность доски и стола одинаков и равен 0,3.
Дано: m1=m2=m=1 кг, α=60°, μ=0,3

Рис.25
Решение. На рисунке укажем все силы, действующие на каждое тело.
Уравнение
движения для любого тела

В проекциях на оси Х и Y:
I тело
x: ma=mg∙sinα - T-Fтр1
y: N1-mg∙cosα=0,
но Fтр1=μN1=μmg∙cosα, тогда
ma=mg∙sinα - T- μmg∙cosα. (1)
II тело
x: ma= T-Fтр1
y: N2-mg =0,
но Fтр2=μN2=μmg, тогда
ma= T- μmg. (2)
Решая систему уравнений (1) и (2),получим

T=m(a+μg).
a=2 м/с; Т=5 Н.
Пример 13. Две гири массами m1=2 кг и m2=1 кг соединены нитью и перекинуты через невесомый блок (рис.26). Найти ускорение, с которым движутся гири, и силу натяжения нити. Трением в блоке пренебречь.

Рис.26
Решение. Условие невесомости и нерастяжимости нити позволяет сделать вывод о том, что сила натяжения нити на всех участках одинакова и грузы движутся с одинаковым ускорением, т.е. T=T1=T2; a=a1=a2. Запишем законы движения для каждого груза.

Выберем направление оси y вниз и спроецируем на нее силы и ускорения:
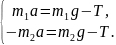
Отсюда


Пример 14.
Три груза массами
 соединены невесомыми нерастяжимыми
нитями (рис. 27). Нити переброшены через
невесомые блоки, закрепленные на
трапециевидном твердом теле ABCD
массы
соединены невесомыми нерастяжимыми
нитями (рис. 27). Нити переброшены через
невесомые блоки, закрепленные на
трапециевидном твердом теле ABCD
массы
 .
Первый груз перемещается вниз по закону
.
Первый груз перемещается вниз по закону
 ,
приводя в движение всю систему. Определить
закон движения тела ABCD
вдоль гладкой горизонтальной плоскости
и его давление на эту плоскость. Угол
BAD
равен
,
приводя в движение всю систему. Определить
закон движения тела ABCD
вдоль гладкой горизонтальной плоскости
и его давление на эту плоскость. Угол
BAD
равен
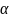 ,
в начальный момент времени система
покоилась.
,
в начальный момент времени система
покоилась.

Рис.27
Решение.
На
данную систему
(тело ABCD
с закрепленными на нем блоками и грузами,
соединенными нитями) действуют следующие
внешние силы: вес тела
 ,
веса грузов
,
веса грузов
 и сила нормальной реакции гладкой
плоскости N
(см. рис. 27). Согласно теореме о
движении центра масс,
и сила нормальной реакции гладкой
плоскости N
(см. рис. 27). Согласно теореме о
движении центра масс,
 (1)
(1)
где
 .
.
В
проекции на горизонтальную ось Ox
соотношение (1) дает:
 .
Следовательно,
.
Следовательно,
 .
Постоянная C1=0,
так как в начальный момент времени
система покоилась. Но тогда хс = const
или хс(t) =
хс(0)
для любого момента времени t,
следовательно,
.
Постоянная C1=0,
так как в начальный момент времени
система покоилась. Но тогда хс = const
или хс(t) =
хс(0)
для любого момента времени t,
следовательно,

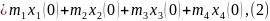
где
 – абсциссы центров масс грузов и тела.
– абсциссы центров масс грузов и тела.
Выберем
начало O
системы координат Oxy
так, чтобы
 ,
т.е. так, что ось Oy
проходит через центр масс тела ABCD
в начальный момент времени. В этой
системе отсчета координаты грузов и
тела связаны соотношениями
,
т.е. так, что ось Oy
проходит через центр масс тела ABCD
в начальный момент времени. В этой
системе отсчета координаты грузов и
тела связаны соотношениями


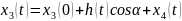 .
.
Подставляя
эти соотношения в уравнение (2), получим
закон движения тела ABCD:
 .
Знак "минус" означает, что призма
перемещается влево относительно
плоскости.
.
Знак "минус" означает, что призма
перемещается влево относительно
плоскости.
Давление
тела ABCD
на плоскость с точностью до знака
совпадает с нормальной реакцией
плоскости. Уравнение для ее определения
получается, если спроектировать (1) на
ось
 .
Откуда
.
Откуда
 (3)
(3)
где ордината центра масс системы определяется соотношением
Myc = m1y1 + m2y2 + m3y3 + m4y4. (4)
Здесь
 – ординаты центров масс грузов и тела.
Для нахождения yc
продифференцируем дважды по времени
равенство (4), учитывая, что
– ординаты центров масс грузов и тела.
Для нахождения yc
продифференцируем дважды по времени
равенство (4), учитывая, что
 ,
,
 .
.
Подставляя полученное в уравнение (3), находим
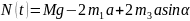 .
.
