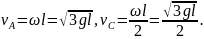В замкнутой системе энергия может переходить из одних видов в другие и передаваться от одного тела к другому, но ее общее количество остается неизменным.

Это один из фундаментальных законов природы. Он подтверждает положение материализма о том, что движение является неотъемлемой частью материи, что оно неуничтожимо, а лишь преобразуется из одной формы в другую. Согласно всеобщему закону сохранения и превращения энергии уменьшение или увеличение полной механической энергии системы в точности компенсируется увеличением или уменьшением какого-либо другого вида энергии.

Энергия никуда не исчезает и не появляется вновь, а лишь переходит от одного тела к другому или превращается из одного вида в другой.

Механическая система будет консервативной, если действующие на нее силы потенциальны, например сила тяжести, силы упругости. В консервативных механических системах с помощью интеграла энергии можно проводить проверку правильности составления дифференциальных уравнений движения. Если система консервативна, а условие (3) не выполняется, значит при составлении уравнений движения допущена ошибка.

В замкнутой системе тел, силы взаимодействия в которой консервативные, взаимные превращения механической энергии в другие виды отсутствуют. Такие системы называются замкнутыми консервативными системами.

Интегралом энергии можно воспользоваться для проверки правильности составления уравнений и другим способом, без вычисления производной. Для этого следует после проведения численного интегрирования уравнений движения вычислить значение полной механической энергии для двух различных моментов времени, например, начального и конечного. Если разница значений окажется сопоставимой с погрешностями вычислений, это будет свидетельствовать о правильности используемых уравнений.

Методические указания по решению задач с применением законов сохранения.

Приведем содержание метода применения законов изменения и сохранения энергии, импульса и момента импульса в виде предписания алгоритмического типа.

1. Выяснить, какие процессы описаны в условии задачи. Для каждого процесса ввести обозначения параметров начального и конечного состояний. Последующие операции алгоритма выполнять для каждого процесса.

2. Указать, какие тела включаем в систему тел.

3. Выбрать систему отсчета - инерциальную или неинерциальную.

4. Установить силы, действующие на каждое тело системы, при переходе из одного состояния в другое. Провести анализ сил, выделив внешние и внутренние, потенциальные и диссипативные.

5. Установить, какой закон следует применять при решении данной задачи. Для этого произвести анализ правой части в выражениях (1), (2), (4), (6).

6. Если энергия, импульс или момент импульса изменяются при рассматриваемом процессе, записать выражения для работы, импульса силы, импульса момента силы.

7. Записать выражения для энергии, импульса или момента импульса каждого тела в отдельности и всей системы в начальном и конечном состояниях.

8. Применить соответствующие законы для каждого процесса.

9. Если необходимо, установить уравнения кинематической связи.

10. Проверить, является ли система уравнений полной, решить ее в общем виде.

11. Проанализировать полученный результат.

Примечания: В приведенных ниже примерах решения задач

- не акцентируется внимание на выполнении пункта 1, если происходит один процесс;

- не обсуждается вопрос о выборе системы отсчета, если рассматривается движение относительно Земли (инерциальной системы отсчета);

- не затрагивается вопрос о характере взаимодействия тел системы, если подобный анализ производился в предыдущих задачах.

Пример 6. Какую скорость надо сообщить точке М стержня, прикрепленного верхним концом с помощью шарнира О к неподвижной поверхности (рис.10), чтобы стержень совершил четверть оборота?

Рис.10

Решение. В первом, вертикальном, положении кинетическая энергия стержня, начавшего вращаться вокруг оси О,

Во втором положении, где стержень достигнет горизонтального положения и остановится на мгновение, Т₂ = 0.

Работу совершит только вес стержня Р: A=-Ph=-Pl/2. По теореме получим уравнение , из которого следует _.

Пример 7. Механическая система состоит из двух шаров A и B, связанных с шарниром O и ползуном C невесомыми стержнями (рис.11).

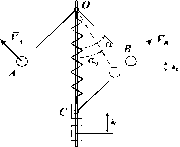
Рис.11

Массы шаров и ползуна одинаковы и равны m=0,2 кг. Стержни имеют одинаковую длину l= 0,3 м. Между шарниром и ползуном установлена пружина жесткостью c =100 Н/м, длина которой в недеформированном состоянии равна l (рис.8). Требуется определить зависимость скоростей движения шаров от угла отклонения стержней от вертикали 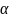и найти максимальное отклонение, если в начальный момент времени система покоилась, а угол составлял .

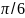Решение. Кинетическая энергия системы складывается из кинетических энергий трех тел, которые по условию могут рассматриваться как материальные точки.

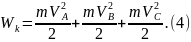
Скорости шаров пропорциональны угловой скорости вращения стержней OA и OB

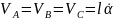
Скорость ползуна нетрудно определить, если учесть, что

.

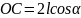Тогда

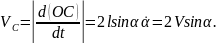
Подставляя выражения для скоростей в (4), получим зависимость кинетической энергии системы от скоростей шаров V и угла отклонения стержней

(5)

Определим работу, которую совершат все силы, приложенные к системе при ее перемещении из начального положения в конечное. Работа сил тяжести определяется вертикальными перемещениями центров тяжести тел (см. рис.8):

Для вычисления работы силы упругости воспользуемся формулой:

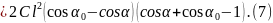
Подставляя выражения (5), (6) и (7) в уравнение теоремы об изменении кинетической энергии, получаем зависимость скорости движения шаров от угла

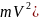
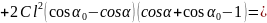
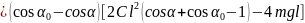
или в явном виде

Если в уравнении 8 скорость V приравнять нулю, можно найти два предельных значения угла , между которыми будет происходить движение системы при заданным начальных условиях:

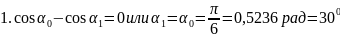
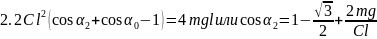
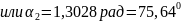
Пример 8. С наклонной плоскости высотой h=1 м и длиною склона l=10 м скользит тело массой в m=1 кг. Найти: 1) кинетическую энергию тела W_k у основания плоскости, 2) скорость тела v у основания плоскости, 3) расстояние s, пройденное телом по горизонтальной части пути до остановки. Коэффициент трения на всем пути считать постоянным и равным 0,05.

Решение. Потенциальная энергия тела при скольжении его с наклонной плоскости переходит в кинетическую энергию и в работу против силы трения, т.е. mgh=mv²/2 + F_трl. Но h=lsin, F_тр=𝜇mg∙cosα, где α - угол наклона плоскости.

1) W_k= mv²/2=mgh- F_трl =mgl(sinα – μcosα). У нас sinα=h/l=0,1, т.е. α=5°44’, следовательно, cosα=0,995.

Подставляя числовые данные задачи, получим W_k=4,9 Дж.

2)

3) Кинетическая энергия тела у основания наклонной плоскости переходит в работу против сил трения на горизонтальной части пути, т.е.

W_k=F_тр∙s =μmgs, откуда s=W_k/μmg=10 м.

Пример 9. Два тела с массами m и 3m движутся во взаимно перпендикулярных направлениях (см.рис.12). После соударения тело массы m остановилось . Какую часть его энергии составляет выделившееся при ударе тепло Q/Е_к1?

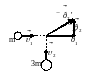
Рис.12

Решение. Так как время соударения мало, то суммарный импульс системы не изменяется.

где 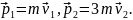Но 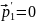, т.к. , поэтому .

Из рисунка видно, что

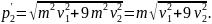
Кинетическая энергия тел до столкновения

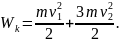
Кинетическая энергия тела с массой 3m после столкновения

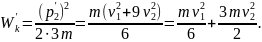
Убыль кинетической энергии означает, что ее часть превратилась во внутреннюю энергию тела, т.е.

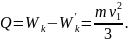
Тогда

т.е. 2/3 кинетической энергии первого тела превратилось в тепло.

Пример 10. Сваю массой m₂=100 кг забивают в грунт копром, масса которого m₁=300 кг. Копер свободно падает с высоты H=4 м и при каждом ударе опускается на h=10 см=0,1 м. Определить силу сопротивления грунта F_c, считая ее постоянной, а удар копра о сваю абсолютно неупругим.

Решение. При падении копра его потенциальная энергия превращается в кинетическую: . Тогда скорость копра в момент удара о сваю v₁=(2gh)^1/2. Удар о сваю неупругий. По закону сохранения импульса m₁v₁=(m₁+m₂)∙v₂. Отсюда v₂=m₁v₁/(m₁+m₂). При движении сваи в грунт действует сила сопротивления, т.е. система незамкнута, поэтому изменение полной энергии системы: ∆Е=А_Fc;

где А_Fc=-F_c∙h - работа силы сопротивления.

Тогда

F_c=94∙10³ H=94 кН.

Пример 11. Груз массой m₁=0,5 кг падает с некоторой высоту на плиту массой m₂=1 кг, укрепленную на пружине жесткостью k=9,8∙10² Н/м. Определить наибольшее сжатие пружины x, если в момент удара груз обладал скоростью v₁=5 м/с. Удар неупругий.

Решение. Так как в системе действуют только силы тяжести и упругости, то система является замкнутой и выполняется закон сохранения энергии. Полная механическая энергия груза вместе с плитой после удара равна потенциальной энергии сжатой пружины:

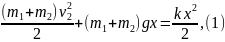
где v₂ - скорость груза и плиты после удара, которую найдем по закону сохранения импульса: m₁v₁=(m₁+m₂)∙v₂.

Откуда

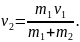
Подставим это выражение в (1):

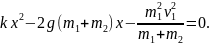
Решая это уравнение, получим х=8,2∙10^-2 м=8,2 см.

Пример 12. Груз массой m=1 кг, висящий на нити, отклоняют на угол α=30° (рис.13). Найти натяжение нити F_н в момент прохождения грузом положения равновесия.

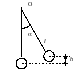
Рис.13

Решение. Натяжение нити в момент прохождения маятником положения равновесия

Кроме того, по закону сохранения энергии 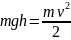, откуда .

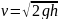Но из рис.13 h=l - lcosα= l(1-cosα).

Тогда

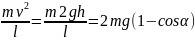
и F_н=mg[1+2 mg(1-cosα)]=12,4 H.

Пример 13. С горки с одной и той же высоты а) соскальзывает без трения брусок, б) скатывается без проскальзывания сплошной цилиндр. Сравните их скорости у основания горки.

Рис.14

Решение. а) Рассмотрим движение бруска. В состоянии I брусок обладал потенциальной энергией (рис.14)

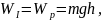
в состоянии II - кинетической энергией поступательного движения

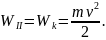
По закону сохранения энергии W_I=W_II получим

откуда скорость бруска равна

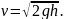
б) Рассмотрим движение цилиндра. В состоянии I цилиндр обладал потенциальной энергией (рис.14)

в состоянии II - кинетической. Однако, в отличие от предыдущего случая цилиндр участвует в двух движениях: поступательном перемещении со скоростью, равной скорости центра масс v_c и вращательном движении вокруг оси, проходящей через центр масс, с угловой скоростью ω. Поэтому полная кинетическая энергия цилиндра состоит из двух частей:

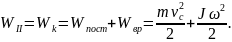
Момент инерции сплошного однородного цилиндра равен , уравнение, связывающее скорости центра масс и угловую скорость имеет вид 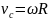. Поэтому

Применяя закон сохранения энергии W_I=W_II получим

откуда скорость цилиндра равна

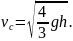
Видно, что

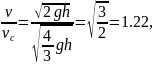
т.е. скорость бруска больше скорости цилиндра в 1,22 раза.

Пример 14. Два одинаковых бруска массой m каждый, соединенные пружиной жесткости k, лежат на горизонтальной плоскости (рис.15). Левый брусок касается вертикальной стенки. Какую минимальную скорость, направленную к стенке, надо сообщить правому бруску, чтобы при обратном движении от стенки он сдвинул левый брусок? Коэффициент трения каждого бруска о плоскость равен μ. Пружина в начальный момент не деформирована.

Рис.15

Решение. На каждый из брусков действуют вертикальные силы тяжести mg и нормального давления N, а также горизонтальные силы упругости со стороны деформированной пружины F и трения F_тр.

Рассмотрим следующие состояния системы тел “бруски + пружина”.

I. В начальном состоянии скорость правого бруска равна v₁, пружина не деформирована.

II. Правый брусок сместился на x₁, его скорость уменьшилась до нуля, пружина сжата и действует на бруски с силой упругости Вследствие действия этой силы правый брусок начинает двигаться в противоположном направлении, проходит первоначальное положение и растягивает пружину. Если сила упругости превышает максимальную силу трения покоя действующую на левый брусок, последний приходит в движение.

III. Третье состояние соответствует началу движения левого бруска, когда пружина растянулась на x₂. Поскольку в условии задачи требуется найти минимальную скорость v₁, позволяющую сдвинуть левый брусок, в данном состоянии скорость правого бруска равна нулю.

Опишем происходящие в системе процессы.

Условие начала движения левого бруска (рис.16) имеет вид или

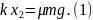
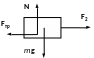
Рис.16

Рассмотрим переход правого бруска из состояния I в состояние II (рис.17). Применим теорему о кинетической энергии, согласно которой ее изменение определяется суммарной работой всех сил, действующих на тело:

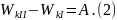
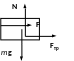
Рис.17

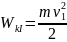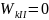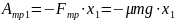Кинетическая энергия в начальном состоянии , в конечном . Работа силы трения: ; работа силы упругости равна изменению потенциальной энергии со знаком “минус”: 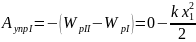; силы тяжести и нормального давления работы не совершают, поскольку они перпендикулярны направлению перемещения. Тогда выражение (2) примет вид

Аналогично описывается переход правого бруска из состояния II в состояние III. На основе теоремы о кинетической энергии имеем

Кинетическая энергия, как в начальном состоянии, так и в конечном, равна нулю. Работа силы трения

Работа силы упругости

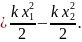
Теорема о кинетической энергии (3) примет вид

или, после сокращения на (x₁+x₂),

Выразим из системы уравнений v₁. Из (1) найдем 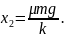Подставляя его в (3а), получим

Наконец, с помощью уравнения (2а) приходим к окончательному результату:

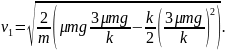
Пример 15. Карандаш длиной l, поставленный вертикально, падает на стол (рис.18). Какую угловую и линейную скорость будут иметь в конце падения середина и верхний конец карандаша?

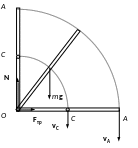
Рис.18

Решение. На карандаш в процессе движения действуют силы тяжести mg, нормального давления N и трения покоя F_тр. Моменты сил нормального давления и трения относительно оси вращения О равны нулю, сила тяжести - потенциальная сила. Следовательно, можно применить закон сохранения энергии.

В начальном состоянии карандаш обладает потенциальной энергией

где h=l/2 - высота, на которой расположен центр масс С.

В конечном состоянии энергия карандаша является кинетической, выражение для которой при вращательном движении имеет вид:

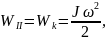
где J - момент инерции тонкого стержня относительно оси, проходящей через его конец, 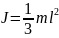; ω - угловая скорость.

Закон сохранения энергии W_II=W_I принимает вид:

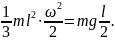
Из полученного уравнения нетрудно выразить угловую скорость карандаша непосредственно перед касанием:

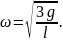
Учитывая связь между линейной и угловой скоростями при вращательном движении по окружности радиуса R: v=ωR, найдем скорости точек А и С: