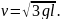- •4) Для самого общего случая движения материальной системы кинетическую энергию помогает вычислить теорема Кенига.
- •Теорема об изменении кинетической энергии системы.
- •В замкнутой системе энергия может переходить из одних видов в другие и передаваться от одного тела к другому, но ее общее количество остается неизменным.
- •Методические указания по решению задач с применением законов сохранения.
- •Вопросы для самопроверки
- •Задачи для самостоятельного решения
Лекция 6. Кинетическая энергия системы.
В данной лекции рассматриваются следующие вопросы:
1. Кинетическая энергия системы. Теорема Кенига.
2. Некоторые случаи вычисления работы.
3. Теорема об изменении кинетической энергии системы.
4. Закон сохранения механической энергии.
5. Методические указания по решению задач с применением законов сохранения.
Изучение данных вопросов необходимо для динамики колебательного движения механической системы, для решения задач в дисциплинах «Теория машин и механизмов» и «Детали машин».
Кинетическая энергия системы.
Кинетической энергией системы называется скалярная величина Т, равная арифметической сумме кинетических энергий всех точек системы

Кинетическая энергия является характеристикой и поступательного и вращательного движения системы, поэтому теоремой об изменении кинетической энергии особенно часто пользуются при решении задач.
Если система состоит из нескольких тел, то ее кинетическая энергия равна, очевидно, сумме кинетических энергий этих тел:
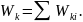
Кинетическая энергия – скалярная и всегда положительная величина.
Найдем формулы для вычисления кинетической энергии тела в разных случаях движения.
1. Поступательное движение. В этом случае все точки тела движутся с одинаковыми скоростями, равными скорости движения центра масс. То есть, для любой точки Vi=VC
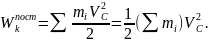
или
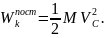
Таким образом, кинетическая энергия тела при поступательном движении равна половине произведения массы тела на квадрат скорости центра масс. От направления движения значение Т не зависит.
2.
Вращательное
движение.
Если тело вращается вокруг какой-нибудь
оси Оz
(см. рис.1), то скорость любой его точки
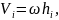 где
где
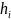 -
расстояние точки от оси вращения, а
-
расстояние точки от оси вращения, а
 -
угловая скорость тела. Подставляя
это значение и вынося общие множители
за скобку, получим:
-
угловая скорость тела. Подставляя
это значение и вынося общие множители
за скобку, получим:
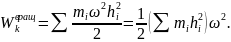
Величина, стоящая в скобке, представляет собою момент инерции тела относительно оси z. Таким образом, окончательно найдем:

т.е. кинетическая энергия тела при вращательном движении равна половине произведения момента инерции тела относительно оси вращения на квадрат его угловой скорости. От направления вращения значение Т не зависит.
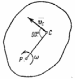
Рис.1
При вращении тела вокруг неподвижной точки кинетическая энергия определяется как (рис.2)

или, окончательно,

где
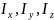 – моменты
инерции тела относительно главных осей
инерции x1,
y1,
z1
в неподвижной
точке О;
– моменты
инерции тела относительно главных осей
инерции x1,
y1,
z1
в неподвижной
точке О;
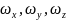 – проекции вектора мгновенной угловой
скорости
– проекции вектора мгновенной угловой
скорости
 на эти оси.
на эти оси.

Рис.2
3. Плоскопараллельное движение. При этом движении скорости всех точек тела в каждый момент времени распределены так, как если бы тело вращалось вокруг оси, перпендикулярной к плоскости движения и проходящей через мгновенный центр скоростей Р (рис.1). Следовательно
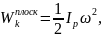
где
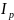 -
момент инерции тела относительно
названной выше оси,
-
угловая скорость тела. Величина
в формуле будет переменной, так как
положение центра Р
при движении тела все время меняется.
Введем вместо
постоянный момент инерции
-
момент инерции тела относительно
названной выше оси,
-
угловая скорость тела. Величина
в формуле будет переменной, так как
положение центра Р
при движении тела все время меняется.
Введем вместо
постоянный момент инерции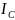 ,
относительно оси, проходящей через
центр масс С
тела. По теореме Гюйгенса-Штейнера
,
относительно оси, проходящей через
центр масс С
тела. По теореме Гюйгенса-Штейнера
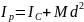 ,
где d=PC.
Подставим это выражение для
.
Учитывая, что точка Р
- мгновенный
центр скоростей, и, следовательно,
,
где d=PC.
Подставим это выражение для
.
Учитывая, что точка Р
- мгновенный
центр скоростей, и, следовательно,
 ,
где
,
где
 -
скорость центра масс С,
окончательно найдем:
-
скорость центра масс С,
окончательно найдем:
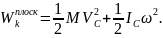
Следовательно, при плоскопараллельном движении кинетическая энергия тела равна энергии поступательного движения со скоростью центра масс, сложенной с кинетической энергией вращательного движения вокруг центра масс.
4) Для самого общего случая движения материальной системы кинетическую энергию помогает вычислить теорема Кенига.
Рассмотрим
движение материальной системы как сумму
двух движений (рис.3). Переносного –
поступательного движения вместе с
центром масс С
и относительного – движения относительно
поступательно движущихся вместе с
центром масс осей x1,
y1,
z1.
Тогда скорость
точек
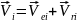 .
Но переносное движение – поступательное.
Поэтому переносные скорости всех точек
равны, равны
.
Но переносное движение – поступательное.
Поэтому переносные скорости всех точек
равны, равны
 .
Значит,
.
Значит,
 и кинетическая энергия будет
и кинетическая энергия будет

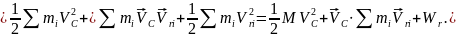

Рис.3
По
определению центра масс его радиус-вектор
в подвижной системе
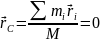 (центр масс находится в начале координат),
значит, и
(центр масс находится в начале координат),
значит, и
 .
Производная по времени от этой суммы
также равна нулю:
.
Производная по времени от этой суммы
также равна нулю:
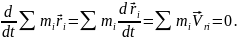
Поэтому, окончательно, кинетическая энергия системы
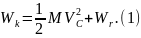
Кинетическая энергия материальной системы равна сумме кинетической энергии при поступательном движении вместе с центром масс и кинетической энергии ее при движении относительно координатных осей, поступательно движущихся вместе с центром масс.
В общем случае движения тела, которое можно рассматривать как сумму двух движений (переносного – поступательного вместе с центром масс С и относительного – вращения вокруг точки С), по теореме Кенига (1) получим

где Ix, Iy, Iz – главные центральные оси инерции тела.
Некоторые случаи вычисления работы.
1)
Работа сил
тяжести, действующих на систему.
Работа силы тяжести, действующей на
частицу весом
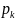 ,
будет равна
,
будет равна
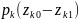 ,
где
,
где
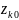 и
и
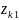 -
координаты, определяющие начальное и
конечное положение частицы. Тогда сумма
работ всех сил тяжести, действующих на
систему, будет равна
-
координаты, определяющие начальное и
конечное положение частицы. Тогда сумма
работ всех сил тяжести, действующих на
систему, будет равна
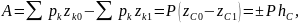
где
Р -
вес системы,
 -
вертикальное перемещение центра тяжести
(или центра масс). Следовательно, работа
сил тяжести, действующих на систему,
вычисляется как работа их равнодействующей
Р на перемещении центра тяжести (или
центра масс) системы.
-
вертикальное перемещение центра тяжести
(или центра масс). Следовательно, работа
сил тяжести, действующих на систему,
вычисляется как работа их равнодействующей
Р на перемещении центра тяжести (или
центра масс) системы.
2) Работа сил, приложенных к вращающемуся телу. Элементарная работа приложенной к телу силы F (рис.4) будет равна
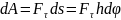 ,
,
так
как
 где
где
 -
угол поворота тела.
-
угол поворота тела.
Но,
как легко видеть,
 .
Будем называть величину
.
Будем называть величину
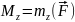 вращающим
моментом.
Тогда получим:
вращающим
моментом.
Тогда получим:
 .
.
Следовательно,
в рассматриваемом случае элементарная
работа равна произведению вращающего
момента на элементарный угол поворота.
Формула справедлива и при действии
нескольких сил, если считать
 .
.
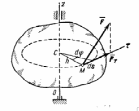
Рис.4
При
повороте на конечный угол
 работа будет равна
работа будет равна
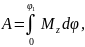
а в случае постоянного момента (Mz=const)

Рисунок
27
Работа, затрачиваемая на изменение скорости вращения, равна изменению кинетической энергии тела:
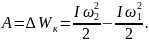
Укажем еще, как в данном случае определяется мощность

Следовательно, при действии сил на вращающееся тело мощность равна произведению вращающего момента на угловую скорость тела. При той же самой мощности вращающий момент будет тем больше, чем меньше угловая скорость.
Если тело катится по горизонтальной поверхности, его кинетическая энергия будет складываться из энергии поступательного движения и энергии вращения (рис.5):
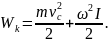

Рис.5
3)
Работа сил
трения, действующих на катящееся
тело. На
колесо радиуса R
(рис.6), катящееся по некоторой плоскости
(поверхности) без скольжения, действует
сила трения F
, препятствующая
скольжению точки касания В
вдоль плоскости.
Элементарная работа этой силы
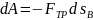 .
Но точка В
в данном случае
является мгновенным центром скоростей
и VB=0.
Так как
.
Но точка В
в данном случае
является мгновенным центром скоростей
и VB=0.
Так как
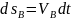 ,
то
,
то
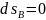 и для каждого элементарного перемещения
dA=0.
и для каждого элементарного перемещения
dA=0.
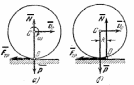
Рис.6
Следовательно, при качении без скольжения, работа силы трения, препятствующей скольжению, на любом перемещении тела равна нулю. По той же причине в этом случае равна нулю и работа нормальной реакции N, если считать тела недеформируемыми и силу N приложенной в точке В (как на рис.6,а).
Сопротивление
качению, возникающее вследствие
деформации поверхностей (pис.6,б),
создает пару ( ),
момент которой M=kN,
где k-
коэффициент
трения качения. Тогда учитывая, что при
качении угол поворота колеса
),
момент которой M=kN,
где k-
коэффициент
трения качения. Тогда учитывая, что при
качении угол поворота колеса
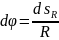 ,
получим:
,
получим:

где
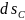 -
элементарное перемещение центра С
колеса.
-
элементарное перемещение центра С
колеса.
Если N= const, то полная работа сил сопротивления качению будет равна
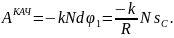
Так как величина k/R мала, то при наличии других сопротивлений сопротивлением качению можно в первом приближении пренебрегать.
Пример 1. Шар массой m =1 кг катится без скольжения по горизонтальной плоскости со скоростью v=2 м/с. Найти кинетическую энергию шара.
Решение. Кинетическая энергия шара в случае качения без скольжения складывается из кинетической энергии поступательного движения центра масс шара и кинетической энергии его вращательного движения, т.е.
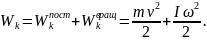
Поскольку
момент инерции шара
 ,
а
,
а
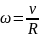 ,
то
,
то
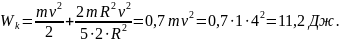
Пример 2. С какой наименьшей высоты должен съехать велосипедист, чтобы по инерции (без трения) проехать дорожку, имеющую форму «мертвой петли» радиусом R = 3 м и не сорваться в верхней точке петли (рис.7)? Масса велосипедиста с велосипедом m = 75 кг, причем на колеса приходится масса m0= 3 кг. Колеса велосипеда считать обручами.

Рис.7
Решение.
На вершине
наклонной плоскости велосипедист
обладает потенциальной энергией WП=mgh.
По закону сохранения энергии этой
энергии должно хватить на подъем на
высоту 2R
( )
и на движение со скоростью v.
Эту скорость найдем, записав II закон
Ньютона для верхней точки «мертвой
петли»,
)
и на движение со скоростью v.
Эту скорость найдем, записав II закон
Ньютона для верхней точки «мертвой
петли»,
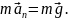
Тогда
 Откуда
Откуда
 .
Обратим внимание на то, что кинетическая
энергия велосипедиста складывается из
кинетической энергии поступательного
движения его центра масс и кинетической
энергии вращательного движения двух
колес его велосипеда, т.е.
.
Обратим внимание на то, что кинетическая
энергия велосипедиста складывается из
кинетической энергии поступательного
движения его центра масс и кинетической
энергии вращательного движения двух
колес его велосипеда, т.е.

Поскольку
колеса – обручи массой m0/2
каждое, то их моменты инерции равны
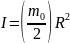 ,
а кинетическая энергия каждого колеса
,
а кинетическая энергия каждого колеса

Отсюда
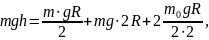
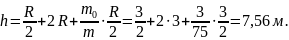
Пример 3. Найти линейные скорости и ускорения центров шара, диска и обруча, скатившихся с наклонной плоскости высотой h = 1 м и углом наклона α=30°. Начальная скорость всех тел v0=0. Сравнить найденные значения со скоростью и ускорением бруска, соскользнувшего с той же наклонной плоскости при отсутствии трения.
Решение. Для всех перечисленных в условии задачи тел закон сохранения энергии записывается в виде WП=Wk. Различие состоит в том, что для шара, диска и обруча кинетическая энергия
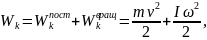
а для бруска
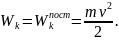
Учитывая,
что моменты инерции перечисленных тел
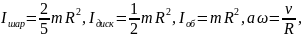 запишем:
запишем:

Ускорения
найдем, воспользовавшись формулой
 ,
где v0=0,
а
,
где v0=0,
а
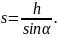 Тогда
Тогда

Пример 4. Колесо, вращаясь равнозамедленно, уменьшило за время t=60 сек, частоту вращения с n1=5 об/с до n2=3 об/с. Колесо считать тонкостенным обручем массой m=1 кг и радиусом R = 0,2 м. Найти угловое ускорение колеса ε, момент сил торможения M, работу сил торможения А и число оборотов N, сделанных колесом за время t = 60 с.
Решение. Поскольку движение колеса является равнозамедленным, то оно описывается формулами

Отсюда модуль углового ускорения
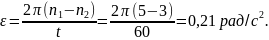
Количество оборотов
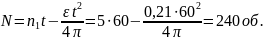
Момент инерции обруча I=mR2=1∙0,22=0,04 кг∙м2.
Из
основного уравнения динамики вращательного
движения

найдем момент сил торможения M=I∙ε=0,04∙0,21=8,4∙10-3 Н∙м.
Работа сил торможения может быть найдена из соображений, что она пошла на изменение кинетической энергии вращающегося колеса.
Тогда,
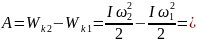
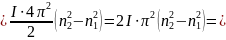

Пример 5. Тонкий однородный стержень длиной l может вращаться относительно горизонтальной оси, проходящей через конец стержня (рис.8). Стержень отклонили на 90° от положения равновесия и отпустили. Определить скорость v нижнего конца стержня в момент прохождения положения равновесия.

Рис.8
Решение. При движении стержня выполняется закон сохранения энергии WП=Wk,
где WП - потенциальная энергия стержня в начальном (поднятом) положении, а Wk - кинетическая энергия в момент прохождения положения равновесия. Обратим внимание на тот факт, что в качестве «нулевого» уровня потенциальной энергии принимается уровень центра масс С стержня в положении равновесия.
Потенциальная энергия WП=mgl/2.
Поскольку
стержень вращается, то его кинетическая
энергия
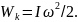
Для нахождения момента инерции I стержня относительно оси, проходящей через его конец, воспользуемся теоремой Штейнера:
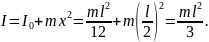
Угловая скорость стержня ω=v/l.
Кинетическая энергия
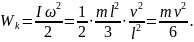
Отсюда
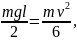
и
скорость нижнего конца стержня в момент
прохождения положения равновесия