Системы линейных алгебраических уравнений

Общий вид системы линейных алгебраических уравнений следующий:

(2),

где а_ij, i=1,...m; j=1,…n—неизвестные величины, называемые коэффициентами системы уравнений. Первый индекс означает номер уравнения, второй—номер неизвестного, при котором стоит коэффициент; b_i, i=1,…m—известные величины, называемые свободными членами, или правыми частями уравнений; x_j, j=1,…n—неизвестные переменные величины (или просто неизвестные).

Система (2)—система линейных уравнений, т.к. все неизвестные входят во все уравнения только в первой степени.

Матрица А, составленная из коэффициентов системы, называется матрицей системы.

Матрица системы, дополненная столбцом свободных членов А│В, называется расширенной матрицей системы:

А= , А│В=

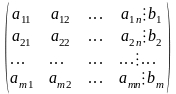
Систему (2) можно записать в матричном виде

АХ=В, где Х= ; В= (3).

Набор чисел ₁, ₂,…, _n — решение системы, если при подстановке x₁= ₁; x₂= ₂;…, x_n= _n все уравнения системы превращаются в верные тождества.

Решить систему значит найти все её решения или доказать, что не существует ни одного её решения. Если решений бесконечное множество, то указать способ нахождения каждого из них.

Система линейных уравнений называется совместной, если она имеет хотя бы одно решение.

Система, не имеющая ни одного решения, называется несовместной.

Если совместная система имеет единственное решение, то она называется определённой, а если более одного решения, то неопределенной.

Две системы алгебраических линейных уравнений называют эквивалентными или равносильными, если они имеют одно и то же множество решений.

Системы n линейных уравнений c n неизвестными.

Общий вид системы уравнений (m=n):

(4).

Матрица А такой системы является квадратной: А= (5)

и она имеет определитель Δ, который называется определителем системы.

I. Метод обратной матрицы.

В матричной форме система уравнений (4) имеет вид (3). Пусть матрица системы А (5) является невырожденной, т.е. существует обратная матрица А^-1 (1). Умножив обе части этого уравнения слева на А^-1, получаем решение системы (4) в матричной форме: Х= А^-1В (6).

Пример: Решить методом обратной матрицы систему уравнений:

Решение: 1)Обозначим

А= ; Х= ; В= .

2) В матричной форме данная система имеет вид: АХ=В. Найдем определитель :

= = = = =

=(-1)·(-1)^{1+2 =}9-4=5 0.

Матрица не вырожденная и существует обратная матрица А^-1.

3) Матрицу А^-1 находим по формуле (1). Получим:

А^-1= .

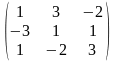4) По формуле (6):

Х= А^-1В= = = 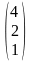, т.е. решение системы (4;2;1)

5) При подстановке полученных значений, получено верное тождество.

Метод Крамера

Теорема (правило Крамера). Пусть Δ — определитель матрицы — определитель матрицы системы А, а Δ_j — определитель, полученный из определителя Δ заменой j-го столбца столбцом свободных членов В. Тогда, если Δ 0, то система линейных уравнений (4) имеет единственное решение, определяемое по формулам

x_i = Δ_j/ Δ, j= 1,2,…,n. (7)

Формулы вычисления неизвестных (7) носят название формул Крамера.

Правило Крамера можно использовать, только когда определитель системы Δ не равен нулю.

Пример: Решить, используя правило Крамера, систему уравнений:

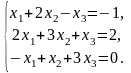
Решение:

Δ= = =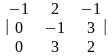 =-11 0

Вычислим дополнительные определители и значения неизвестных:

Δ₁=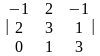 = = - =-22; x₁ = Δ₁/ Δ= (-22)/(-11)= 2.

Δ₂= = = =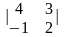11; x₂ = Δ₂/ Δ= 11/(-11)=-1.

Δ₃= = = =-11; x₃ = Δ₃/ Δ= (-11)/(-11)=1.

Путем подстановки можно проверить, что полученное решение Х=(2,-1,1) является верным.