
- •План занятия
- •Глоссарий
- •Алгоритм вычисления обратной матрицы.
- •Ход занятия
- •Основные теоретические сведения по теме: "Матрицы. Основные операции с матрицами"
- •Необходимый для повторения теоретический материал по теме: "Определители второго, третьего и высших порядков. Их свойства и методы вычисления"
- •9. Равенство справедливо
- •Необходимый для повторения теоретический материал по теме: "Решение систем линейных уравнений по формулам Крамера, матричным методом и методом Гаусса"
- •Системы линейных алгебраических уравнений
- •I. Метод обратной матрицы.
- •Метод Крамера
- •Метод Гаусса
- •Литература Основные учебные пособия
- •Дополнительная литература
- •Интернет-ресурсы
ПЛАНЫ
лабораторных занятий
по дисциплине «Математика»
Направление подготовки: 36.03.02 "Зоотехния"
Профили: "Кормление животных и технология кормов",
"Разведение, генетика и селекция животных",
"Технология производства продукции животноводства"
Факультет: зооинженерный
Форма обучения: очная, заочная
1 МОДУЛЬ
Лабораторное занятие №1
Темы: Матрицы. Основные операции с матрицами.
Определители второго, третьего и высших порядков. Их свойства и методы вычисления. Решение систем линейных уравнений по формулам Крамера, матричным методом и методом Гаусса
(2 часа)
Занятие проводится в интерактивной форме – в форме работы малых групп
Учебно-познавательные цели занятия:
осмысление и усвоение правил действий над матрицами;
научить студентов различным приемам вычисления определителей;
ознакомиться с методикой решения систем линейных уравнений, используя методы Крамера, матричный метод и метод Гаусса
Воспитательные цели: Развивать алгоритмическую культуру студентов, повышать интерес к предмету в процессе решения задач
Развивающая цель – развитие творческих способностей студентов.
На лабораторном занятии формируются понятия:
- матрицы ( прямоугольной, квадратной, матрицы-строки, матрицы-столбца, диагональной, единичной, обратной и т.д.)
- определителя второго, третьего и высших порядков;
- решения системы линейных уравнений:
- совместной, несовместной, определенной и неопределенной систем;
- обратной матрицы;
- элементарных преобразований матрицы.
На занятии формируются знания:
- свойств операций над матрицами;
- свойств определителей квадратных матриц;
- формул Крамера;
- матричного метода решения систем;
- метода Гаусса.
умения:
- выполнять операции над матрицами (складывать, умножать на число, перемножать матрицы; транспонировать);
- вычислять определители различными способами;
- находить обратную матрицу для данной невырожденной;
- решать системы линейных уравнений методом Крамера,матричным методом и методом Гаусса.
навыки:
- аргументированного письменного изложения собственной точки зрения;
- критического восприятия информации
компетенции:
- ОК-1 – владение культурой мышления, способностью к восприятию, обобщению и анализу информации, постановке цели и выбору путей ее достижения;
- ОК-20 – способен к решению нестандартных задач в соответствии с потребностями общества;
- ОК-22 – способен к самообучению в течение всей жизни;
- ПК-13 - в организационно-управленческой деятельности способностью анализировать и планировать технологические процессы как объекты управления;
- ПК-30 - владеет математическими методами анализа и умеет применять их в профессиональной деятельности.
Материально-техническое оборудование:
мультимедийный проектор, ноутбук, презентация «Матрицы и определители».
План занятия
1. Инструктаж по ТБ.
2.Проверка знаний студентов — их теоретической готовности к выполнению заданий по каждой из следующих тем:
1. Понятие матрицы. Виды матриц
2. Операции над матрицами и их свойства
3. Понятие определителя второго и третьего порядков
4. Свойства определителей и их вычисление
5. Система трех линейных уравнений с тремя неизвестными
6. Решение системы трех линейных уравнений с тремя неизвестными методом Крамера
7. Решение систем линейных уравнений методом обратной матрицыи методом Гаусса
3. Общее описание задания.
4. Выполнение заданий.
5. Оформление отчета о лабораторной работе.
6. Анализ
Глоссарий
Выучите определения следующих терминов:
матрица, виды матриц, размерность матрицы, сумма двух матриц, свойства операции сложения матриц, умножение матрицы на число, произведение матриц, свойства операции умножения матриц, возведение матрицы в степень, транспонирование матриц, обратная матрица, нахождение обратной матрицы, элементарные преобразования матриц, система линейных уравнений, матричное уравнение, решение матричного уравнения, нахождение решения систем линейных уравнений матричным способом, методом Крамера, решение систем линейных уравнений методом Гаусса.
№ п/п |
Новые понятия |
Содержание |
1 |
2 |
3 |
1 |
Матрица
размера
|
это прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, образующие матрицу, называются ее элементами. |
2 |
Матрица-строка |
это матрица, состоящая из одной строки; |
3 |
Матрица-столбец |
это матрица, состоящая из одного столбца. |
4 |
Квадратная матрица n-го порядка |
это матрица, у которой количество строк равно количеству столбцов и равно n. |
5 |
Диагональная матрица
|
это квадратная матрица, у которой все элементы, кроме элементов, стоящих на главной диагонали равны нулю |
6 |
Единичная матрица
|
это диагональная матрица, у которой элементы, стоящие на главной диагонали равны единице.
|
7 |
Умножение матрицы на число |
Чтобы умножить
матрицу на число |
8 |
Сложение матриц |
Чтобы сложить две матрицы одинакового размера, необходимо сложить соответствующие элементы этих матриц |
9 |
Умножение матриц |
а) Две матрицы можно перемножить тогда и только тогда, когда количество столбцов в первом сомножителе равно количеству строк во втором сомножителе. б)
Произведением
матрицы
матрица
пересечении
i-й
строки и j-го
столбца, равен сумме произведений
элементов i-й
строки матрицы A
и j-го
столбца матрицы B,
т.е.
|
10 |
Транспонирование матрицы |
Чтобы транспонировать матрицу A необходимо ее строки заменить столбцами с теми же номерами. |
11 |
Определитель
квадратной матрицы второго
порядка
A= |
равен разности произведений элементов главной диагонали и элементов побочной диагонали матрицы, т.е. 2= |
12 |
Определитель
квадратной матрицы третьего
порядка A=
|
3=
= |
№ п/п |
Новые понятия |
Содержание |
1 |
2 |
3 |
13 |
Алгебраическим
дополнением элемента
|
называется число, которое находят по формуле:
|
14 |
Минором
k-го
порядка
матрицы A
размера
mхn
( |
называется определитель квадратной матрицы k-го порядка, состоящей из элементов, стоящих на пересечении произвольно выбранных k строк и k столбцов матрицы A. Обозначение: Mk- минор k-го порядка. |
15 |
Ранг матрицы |
Рангом матрицы называют наивысший порядок отличных от нуля миноров этой матрицы. Обозначение: rang A или r(A). |
16 |
Обратная матрица для квадратной матрицы А |
Обратной матрицей для квадратной матрицы A называется матрица A-1, такая, что верно равенство: AA-1=A-1A=E. |
17 |
Вырожденная и невырожденная матрицы |
Квадратная матрица называется вырожденной, если ее определитель равен нулю, в противном случае матрица называется невырожденной. |


 k,
необходимо на это число умножить все
элементы матрицы
k,
необходимо на это число умножить все
элементы матрицы на матрицу
на матрицу
 является
является ,
каждый элемент которой
,
каждый элемент которой
 ,
стоящий на
,
стоящий на .
.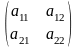
 =
= .
.
 .
.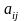 квадратной матрицы A
n-го
порядка
квадратной матрицы A
n-го
порядка ,
, )
)