Тема2.1. Механічний рух та його види. Рівномірний прямолінійний рух. (2 год.)

Мета: познайомити студентів з основною задачею механіки і поняттями матеріальної точки, системи відліку, траєкторії, переміщення та шляху; розкрити характерні особливості прямолінійного рівномірного руху;

розширити й поглибити поняття відносності руху; сформувати навички додавання швидкостей і переміщень;

План.

1. Характеристика механічного руху.

2. Кінематика. Основні поняття кінематики.

3. Відносність механічного руху.

4. Рівномірний рух.

Вивчення нового матеріалу.

Будь-яке фізичне явище або процес в оточенні нас матеріальному світі є закономірний ряд змін, що відбуваються в часі і просторі. Механічний рух, тобто зміна положення цього тіла (чи його частин) відносно інших тіл, - це простий вид фізичного процесу. Механічний рух тіл вивчається в розділі фізики, який називається механікою. Основне завдання механіки - визначити положення тіла у будь-який момент часу.

Одна з основних частин механіки, яка називається кінематикою, розглядає рух тіл без з'ясування причин цього руху. Кінематика відповідає на питання: як рухається тіло? Іншою важливою частиною механіки є динаміка, яка розглядає дійстві одних тіл на інших як причину руху. Динаміка відповідає на питання: чому тіло рухається саме так, а не інакше?

Механіка - одна з самих древніх наук. Певні знання в цій області були відомі задовго до нової ери (Арістотель (IV століття до н. е.), Архімед (III ст. до н.е.)). Проте, якісне формулювання законів механіки почалося тільки в XVII столітті н.е., коли Г. Галілей відкрив кінематичний закон складання швидкостей і встановив закони вільного падіння тел. Через декілька десятиліть після Галілея великого И. Ньютона (1643-1727) сформулював основні закони динаміки.

У механіці Ньютона рух тіл розглядається при швидкостях, багато менше швидкості світла в порожнечі. Її називають класичною або ньютонівською механікою на відміну від релятивістської механіки, створеної на початку XX століття головним чином завдяки роботам А. Ейнштейна (1879-1956).

У релятивістській механіці рух тіл розглядається при швидкостях, близьких до швидкості світла. Класична механіка Ньютона є граничним випадком релятивістської при υ << c.

Кінематика. Основні поняття кінематики.

Кінематикою називають розділ механіки, в якому рух тіл розглядається без з'ясування причин, що його викликають.

Механічним рухом тіла називають зміну його положення в просторі відносно інших тіл з часом.

Механічний рух відносний. Рух одного і того ж тіла відносно різних тіл виявляється різним. Для опису руху тіла треба вказати, по відношенню до якого тіла розглядається рух. Це тіло називають тілом відліку.

Система координат, пов'язана з тілом відліку, і годинник для відліку часу утворює систему відліку, що дозволяє визначати положення рухомого тіла у будь-який момент часу.

У Міжнародній системі одиниць (СІ) за одиницю довжини прийнятий метр, а за одиницю часу - секунда.

Всяке тіло має певні розміри. Різні частини тіла знаходяться в різних місцях простору. Проте, в багатьох завданнях механіки немає необхідності вказувати положення окремих частин тіла. Якщо розміри тіла малі в порівнянні з відстанями до інших тіл, то це тіло можна вважати його матеріальною точкою. Так можна поступати, наприклад, при вивченні руху планет навколо Сонця.

Якщо усі частини тіла рухаються однаково, то такий рух називається поступальним. Поступально рухаються, наприклад, кабіни в атракціоні "Колесо огляду", автомобіль на прямолінійній ділянці шляху і т. д. При поступальній ході тіла його також можна розглядати як матеріальну точку.

Тіло, розмірами якого в цих умовах можна нехтувати, називається матеріальною точкою.

Поняття матеріальної точки грає важливу роль в механіці.

Переміщаючись з часом з однієї точки в іншу, тіло (матеріальна точка) описує деяку лінію, яку називають траєкторією руху тіла.

Положення матеріальної точки в просторі у будь-який момент часу (закон руху) можна визначати або за допомогою залежності координат від часу x = x (t), y = y (t), z = z(координатний спосіб), або за допомогою залежності від часу радіус-вектора /(векторний спосіб), проведеного з початку координат до цієї точки (мал. 1).

Малюнок 1

Переміщенням тіла називають спрямований відрізок прямої, що сполучає початкове положення тіла з його наступним положенням. Переміщення є векторна величина.

Пройдений шлях l дорівнює довжині дуги траєкторії, пройденої тілом за деякий час t. Шлях - скалярна величина.

Якщо рух тіла розглядати протягом досить короткого проміжку часу, то вектор переміщення виявиться спрямованим по дотичній до траєкторії в цій точці, а його довжина дорівнюватиме пройденому шляху.

У разі досить малого проміжку часу Δt пройдений тілом шлях Δl майже співпадає з модулем вектора переміщення При русі тіла по криволінійній траєкторії модуль вектора переміщення завжди менше пройденого шляху (мал. 2).

Малюнок 2.

Для характеристики руху вводиться поняття середньої швидкості :

У фізиці найбільший інтерес представляє не середня, а миттєва швидкість, яка визначається як межа, до якої прагне середня швидкість на нескінченно малому проміжку часу Δt, :

Миттєва швидкість тіла в будь-якій точці криволінійної траєкторії спрямована по дотичній до траєкторії в цій точці. Відмінність між середньою і миттєвою швидкостями показано на мал. 3.

Малюнок 3.

При русі тіла по криволінійній траєкторії його швидкість змінюється по модулю і напряму. Зміна вектора швидкості за деякий малий проміжок часу Δt можна задати за допомогою вектора (мал. 4).

Вектор зміни швидкості за малий час Δt можна розкласти на дві складові: спрямовану уздовж вектора (дотична складова), і спрямовану перпендикулярно вектору (нормальна складова).

Малюнок 4.

Відносність руху

Рух тіл можна описувати в різних системах відліку. З точки зору кінематики усі системи відліку рівноправні. Проте кінематичні характеристики руху, такі як траєкторія, переміщення, швидкість, в різних системах опиняються різними. Величини, залежні від вибору системи відліку, в якій виробляється їх вимір, називають відносними.

Нехай є дві системи відліку. Система XOY умовно вважається нерухомою, а система X'O'Y' рухається поступально по відношенню до системи XOY з швидкістю υ. Система XOY може бути, наприклад, пов'язана із Землею, а система X'O'Y' - з рухомою по рейках платформою (мал. 5).

Малюнок 5

Нехай людина перейшла по платформі за деякий час з точки A в точку B. Тоді його переміщення відносно платформи відповідає вектору а переміщення платформи відносно Землі відповідає вектору З мал. 5 видно, що переміщення людини відносно Землі відповідатиме вектору :

У разі, коли одна з систем відліку рухається відносно іншої поступально (як на мал. 5) з постійною швидкістю цей вираз набирає вигляду:

Якщо розглянути переміщення за малий проміжок часуΔt, то, розділивши обидві частини цього рівняння на Δt і потім перейшовши до межі при Δt → 0 отримаємо:

Тут - швидкість тіл в "нерухомій" системі відліку XOY, - швидкість тіла в "рухомій" системі відліку X'O'Y'. Швидкості іноді умовно називають абсолютною і відносною швидкостями.

Співвідношення (*) виражає класичний закон складання швидкостей :

Абсолютна швидкість тіла дорівнює векторній сумі його відносної швидкості і переносної швидкості рухомої системи відліку.

Рівномірний рух.

Простим видом механічного руху є рух тіла уздовж прямої лінії з постійною по модулю і напряму швидкістю. Такий рух називається рівномірним. При рівномірному русі тіло за будь-які рівні проміжки часу проходить рівні шляхи. Для кінематичного опису рівномірного прямолінійного руху координатну вісь OX зручно розташувати по лінії руху. Положення тіла при рівномірному русі визначається завданням однієї координати x. Вектор переміщення і вектор швидкості завжди спрямовані паралельно координатній осі OX. Тому переміщення і швидкість при прямолінійному русі можна спроектувати на вісь OX і розглядати їх проекції як величини алгебри.

Якщо в деякий момент часу t1 тіло знаходилося в точці з координатою x1, а в пізніший момент t2 - в точці з координатою x2, то проекція переміщення Δs на вісь OX за час Δt = t2 - t1 рівна

Δs = x2 - x1.

Ця величина може бути і позитивною і негативною залежно від напряму, в якому рухалося тіло. При рівномірному русі уздовж прямої модуль переміщення співпадає з пройденим шляхом. Швидкістю рівномірного прямолінійного руху називають відношення

Якщо υ > 0, то тіло рухається у бік позитивного напряму осі OX; при υ < 0 тіло рухається в протилежному напрямі.

Залежність координати x від часу t (закон руху) виражається при рівномірному прямолінійному русі лінійним математичним рівнянням :

x (t) = x0 + υt

У цьому рівнянні υ = const - швидкість руху тіла, x0 - координата точки, в якій тіло знаходилося у момент часу t = 0. Графік закону руху x(t) є прямою лінією. Приклади таких графіків показані на мал.6.

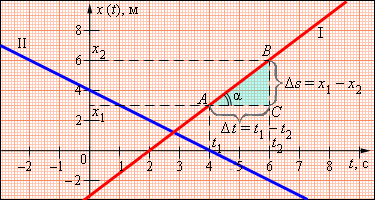
Малюнок 6

Для закону руху, зображеного на графіці I (мал. 6), при t = 0 тіло знаходилося в точці з координатою x0 = - 3. Між моментами часу t1 = 4 з і t2 = 6 з тіло перемістилося від точки x1 = 3 м до точки x2 = 6 м. Таким чином, за Δt = t2 - t1 = 2 з тіло перемістилося на Δs = x2 - x1 = 3 м. Отже, швидкість тіла складає

Величина швидкості виявилася позитивною. Це означає, що тіло рухалося в позитивному напрямі осі OX. Звернемо увагу, що на графіці руху швидкість тіла може бути геометрично визначена як відношення сторін BC і AC трикутника ABC (см. рис. 1.3.1)

Чим більше кут α, який утворює пряма з віссю часу, тобто чим більше нахил графіка (крутизна), тим більше швидкість тіла. Іноді говорять, що швидкість тіла дорівнює тангенсу кута α нахилу прямої x (t). З точки зору математики це твердження не цілком коректно, оскільки сторони BC і AC трикутника ABC мають різну розмірність: сторона BC вимірюється в метрах, а сторона AC - в секундах.

Аналогічним чином для руху, зображеного на мал. 1.3.1 прямій II, знайдемо x0 = 4 м, υ = - 1 м/с.

На мал. 1.3.2 закон руху x (t) тіла зображений за допомогою відрізків прямих ліній. У математиці такі графіки називаються криволінійними. Такий рух тіла уздовж прямої не є рівномірним. На різних ділянках цього графіка тіло рухається з різними швидкостями, які також можна визначити по нахилу відповідного відрізку до осі часу. В точках зламу графіка тіло миттєво змінює свою швидкість. На графіці (мал. 7) це відбувається в моменти часу t1 = - 3 з, t2 = 4 з, t3 = 7 з і t4 = 9 с. По графіку руху неважко знайти, що на інтервалі (t2; t1) тіло рухалося із швидкістю υ12 = 1 м/з, на інтервалі (t3; t2) - із швидкістю υ23 = - 4/3 м/з і на інтервалі (t4; t3) - із швидкістю υ34 = 4 м/с.

Слід зазначити, що при криволінійному законі прямолінійного руху тіла пройдений шлях l не співпадає з переміщенням s. Наприклад, для закону руху, зображеного на мал. 1.3.2, переміщення тіла на інтервалі часу від 0 з до 7 з дорівнює нулю (s = 0). За цей час тіло пройшло шлях l = 8 м.

Малюнок 7

Запитання для самоперевірки:

1. У чому полягає основна задача механіки?

2. Що таке механічний рух?

3. Що вивчає кінематика?

4. Що називають системою відліку? З чого вона складається?

5. У якій системі відліку простіше описувати: а) рух потяга?; б) рух планет?

6. Що розуміють під матеріальною точкою?

7. Коли тіло можна вважати матеріальною точкою, а коли – не можна? Наведіть приклади.

8. Що таке траєкторія? На які види поділяють рухи за видами траєкторії?

9. Чи залежить вид траєкторії від вибору системи відліку?

10. Що таке шлях?

11. Що таке переміщення?

12. Чим відрізняється шлях від переміщення?