
- •Математический аназиз
- •Содержание
- •Введение
- •Условия задач расчетно-графической работы Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6
- •Задание 7
- •Задание 8
- •Задание 9
- •Задание 10
- •Задание 11
- •Методические указания к выполнению расчетно-графической работы Задание 1
- •Задание 2
- •Задание 3
- •Задание 4
- •Задание 5
- •Задание 6
- •Задание 7
- •Задание 8
- •Задание 9
- •Задание 10
- •Задание 11
- •Теоретические вопросы к экзамену
- •Дополнительная
Задание 5
Найти работу силы F при перемещении вдоль линии L от точки М к точке N.
1 |
|
16 |
|
2 |
|
17 |
|
3 |
|
18 |
|
4 |
|
19 |
|
5 |
|
20 |
|
6 |
|
21 |
|
7 |
|
22 |
|
8 |
|
23 |
|
9 |
|
24 |
|
10 |
|
25 |
|
11 |
|
26 |
|
12 |
|
27 |
|
13 |
|
28 |
|
14 |
|
29 |
|
15 |
|
30 |
|
Задание 6
Дано число z.
1. Записать число z в тригонометрической и показательной формах.
2.
Найти
 .
.
3.
Найти
 .
.
1 |
|
11 |
|
21 |
|
2 |
|
12 |
|
22 |
|
3 |
|
13 |
|
23 |
|
4 |
|
14 |
|
24 |
|
5 |
|
15 |
|
25 |
|
6 |
|
16 |
|
26 |
|
7 |
|
17 |
|
27 |
|
8 |
|
18 |
|
28 |
|
9 |
|
19 |
|
29 |
|
10 |
|
20 |
|
30 |
|
Задание 7
Решить дифференциальное уравнение.
1 |
|
16 |
(x2-3)y'=3-4y |
2 |
sin2x(2-y2)+y'=0 |
17 |
(x2-2)y'=4+y2 |
3 |
сos24y+(5-x2)y'=0 |
18 |
|
4 |
cos2x+e2yy'=0 |
19 |
y2+y' |
5 |
(3-y2) |
20 |
ylnye2x+y'=0 |
6 |
|
21 |
sin22x(2-y2)=y' |
7 |
y3+(x2-4)y'=0 |
22 |
xe2x(5-y2)=y' |
8 |
y'sin3ye2x+x=0 |
23 |
1=y'(3-x2)sin2y |
9 |
y2+e2xy'=2 |
24 |
exy'=1-y2 |
10 |
y'(x2-5)=2y+1 |
25 |
(3-x2)y'-9=y2 |
11 |
y'lny+x2=7 |
26 |
yy'=eyx |
12 |
y'lnxx+y2=3 |
27 |
x |
13 |
y' |
28 |
(1+ex)y'=y ex |
14 |
|
29 |
2x+2xy2+ |
15 |
y'cos22x=2-y2 |
30 |
yy' |
Задание 8
Найти частное решение дифференциального уравнения, удовлетворяющее данному начальному условию.
1 |
xy'-2y-2x4=0, y(1)=2 |
16 |
|
2 |
y' -y=e3x x, y(0)=5 |
17 |
y'-y cos2x=cos2xe(1/2)sin2x, y(0)=1 |
3 |
|
18 |
|
4 |
|
19 |
|
5 |
y'+2(tg2x)y=sin4x, y(0)=1 |
20 |
|
6 |
y'-2xy=x3, y(0)=1 |
21 |
|
7 |
|
22 |
|
8 |
|
23 |
y'-5y=x, y(0)=1 |
9 |
|
24 |
y'-2(ctgx)y=1, y(/4)=0 |
10 |
|
25 |
y'+2(tgx)y=1, y(/4)=3 |
11 |
y'-y cosx=cosx esinx , y(0)=3 |
26 |
|
12 |
|
27 |
y'-y
sinx= |
13 |
y'-y sin2x=sin2x e-(1/2)cos2x, y(0)= 0 |
28 |
y'+y cosx= e-sinx, y(1)=-1 |
14 |
y'+2xy=-2x3, y(1)= |
29 |
y'+ |
15 |
|
30 |
|


























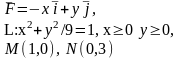




















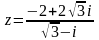
















 +y'=0
+y'=0 =0
=0



















 sin2x,
y(1)=1
sin2x,
y(1)=1
 ,
y(1)=1
,
y(1)=1
