3) Види рівноваги (рис. 16):

Стійка – при малому відхиленні від положення рівноваги виникає рівнодійна сил,

що повертає тіло в це положення.

Нестійка – при малому відхиленні від положення рівноваги виникає рівнодійна сил,

напрямлена від положення рівноваги.

Байдужа – у будь-якому положенні тіла рівнодійна прикладених сил дорівнює 0.

Принцип мінімума потенціальної енергії:

стійке те положення тіла, у якого потенціальна енергія має мінімальне значення.

Стійка рівновага тіл на плоскій поверхні тим більша, чим більша площа опори

і нижче центр тяжіння.

4) Центр тяжіння і центр мас.

Центр тяжіння – це точка прикладання сили тяжіння. Тіло, підперте в центрі

тяжіння, перебуватиме в рівновазі.

Центр мас – це точка перетину прямих, уздовж яких діють сили, що в інерціальній

системі відліку (ІСВ) зумовлюють поступальний рух тіла. Для однорідних тіл

правильної геометричної формицентр мас збігається з геометричним центром

симетрії тіла.

В однорідному гравітаційному полі центри мас і тяжіння збігаються.

Координати центра тяжіння (рис. 16):

, , ,

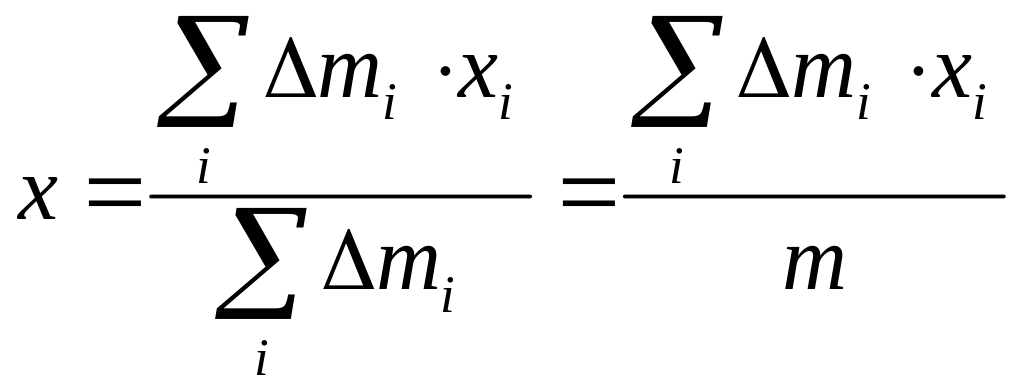або у векторній формі запису:

Рис. 17

5) Прості механізми.

Важіль – невагомий жорсткий стержень, що має вісь обертання.

Блок – невагоме колесо із жолобом, закріплене в обоймі. По жолобу протягують

мотузку або трос.

Похила площина служить для підняття чи опускання вантажів.

Важіль	Блок		Похила площина
Змінює напрям дії сили, дає виграш у силі:	Нерухомий блок змінює напрям дії сили, не дає виграшу в силі:	Рухомий блок не змінює напряму дії сили, дає виграш в силі у 2 рази:	Змінює напрям дії сили, дає виграш у силі:

«Золоте правило» механіки – жоден із простих механізмів не дає виграшу в роботі:

вигравши у силі, у стільки ж разів програємо у відстані.

Механічні коливання і хвилі.

1) Види коливань.

Коливання – рухи або зміни стану, що точно або приблизно повторюються з часом.

Коливальна система – система тіл, у якій можуть виникати вільні коливання. Сили,

що діють між тілами коливальної системи, називають внутрішніми.

Вільні коливання – коливання, що відбуваються під дією лише внутрішніх сил

системи після того, як її вивести зі стану рівноваги. Вільні коливання здійснюють

тіло на підвісі або тягарець на пружині.

Для виникнення вільних коливань необхідні такі умови:

а) при виведенні тіла з положення рівноваги виникає сила (рівнодійна сил), що

повертає тіло у це положення;

б) втрати енергії в системі незначні.

Затухаючі коливання – коливання, в яких присутні сили тертя. Тільки в межах

невеликого інтервалу часу зменшенням амплітуди можна нехтувати і вважати

(приблизно) коливання незатухаючими. При затухаючих коливаннях рух є

неперіодичним. Із збільшенням сил тертя коливання затухають швидше.

Вимушеними називають незатухаючі коливання, що відбуваються під дією

зовнішньої сили, що періодично змінюється.

Резонанс – явище різкого зростання амплітуди вимушених коливань за умови,

що частота дії зовнішньої періодичної сили збігається з частотою вільних коливань

системи.

Автоколивання відбувається у системі, яка містить джерело енергії і сама регулює

надходження енергії до тіла, що здійснює коливання.

Рис. 18 Рис. 19

2) Пружинний маятник.

Пружинний маятник – коливальна система, в якій коливання відбувається під дією

сили пружності (рис. 18).

Період коливань пружинного маятника:

,

де - маса вантажу; - жорсткість пружини або системи пружин.

Рівняння коливання вантажу на пружині:

,

де - прискорення вантажу; - координата вантажу відносно положення рівноваги;

- циклічна частота коливань вантажу.

3) Математичний маятник.

Математичний маятник – модель коливальної системи, що складається з

матеріальної точки, маса якої , підвішеної на нерозтяжній невагомій нитці

завдовжки (рис. 19). Реальна така модель називається фізичним маятником.

Коливання математичного маятникає гармонічним, якщо .

Період коливань математичного маятника:

Якщо маятник рухається з прискоренням , то

, де :

- прискорення напрямлене вгору;

- прискорення напрямлене вниз;

- прискорення напрямлене горизонтально.

Рівняння руху маятника при малих кутах відхилення від положення рівноваги:

, ,

де - тангенціальне прискорення точки; - величина дуги зміщення рівноваги;

- циклічна частота коливань маятника; - прискорення вільного падіння.