
- •3.Абсолютна величина числа
- •4.Межі числових множин
- •5. Множина комплексних чисел
- •6.Геометрична інтерпретація комплексних чисел
- •13. Системи визначника n-го порядку. Властивості визначників
- •14.Системи лінійних неоднорідних рівнянь. Роз’язання систем лінійних неоднорідних методом Крамера
- •15. Лінійні простори
- •16. Евклідові простори. Ортогоналізація в евклідовому просторі
- •17. Характеристичні ( власні) числа та власні вектори матриці
- •18. Квадратичні форми
- •4.5. Границя числової послідовності.
- •Загальні властивості збіжних послідовностей.
- •Безмежно мала величина та її властивості
- •4.6. Границя функції. Теореми про границі. Ліва та права границі.
- •4 .7. Дві визначні границі.
- •50.Число e
- •51.Границя функцій
- •52.Теореми границі функції
- •53.Перша визначна границя функції:
- •54. Друга визначна границя функції:
- •55.Нескінченно малі і великі функції
- •Розриви першого роду. Якщо в точці функція має скінченну ліву й скінченну праву границю і вони рівні між собою, тобто
- •Але відмінні від значення функції в точці або значення не існує, то точка називається точкою усувного розриву функції
- •60. Операції над неперервними функціями
- •62. Перша і друга теореми Вейєрштрасса.
- •63. Поняття рівномірної неперервності. Теорема Кантора.
- •64. Поняття оберненої функції. Теорема про неперервність оберненої функції.
- •65. Поняття похідної, геометричний зміст похідної. Права і ліва похідні.
- •6 6. Поняття диференційовності функції в точці. Зв'язок між диференційовністю та неперервністю функції.
- •67. Похідна суми, частки, добутку функцій.
- •70 Таблиця похідних основних елементарних функцій
- •Диференціал функції
- •86.Асимптоти кривої. Загальна схема дослідження функції.
- •87.Загальний план дослідження функції та побудови її графіків.
- •88, 89. Функції двох змінних
- •90. Неперевність функції багатьох змінних
- •91. Основні властивості непервності функції
- •101.Формула тейлора для функції багатьох змінних
- •102.Поняття неявної функції. Теорема існування і диференційованості неявної функції
- •103.Екстремум функції двох та багатьох змінних. Необхідні і достатні умови екстремуму
- •104.Екстремуми функцій багатьох змінних. Умовний екстремум.
52.Теореми границі функції
Теорема(про єдність границі функції в точці). Якщо в точці а функція y=f(x) має границю, то ця границя єдина.
Теорема:
Нехай
функцій f(x),g(x)
і h(x)
визначені на множині Х з точкою згущення
а, і для всіх х є Х виконується нерівність
f(x)<h(x)<g(x)
або f(x)=h(x)=g(x).
Якщо
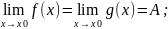
то
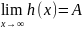 Теорема:
Теорема:
Якщо функції y=f(x) і y=g(х) мають границю в точці Хо то їхня алгебраїчна сума,добуток і частка (при умові що границя знаменника не дорівнює О) також мають границю в цій точці і виконуються рівності :
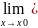
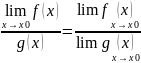
Доведення:
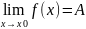
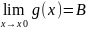

53.Перша визначна границя функції:
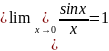
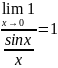
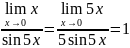
54. Друга визначна границя функції:


55.Нескінченно малі і великі функції
Функція α(х) називають нескінченно малу функцію в точці Хо,якщо границя дорівнює нулю :
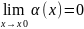
Теорема
Алгебраїчна сума і добуток скінченного числа нескінченно малих функцій в точці Хо є нескінченно малою функцією
Теорема
Добуток обмеженої функції і нескінченно малої функції в точці Хо є нескінченно малою функцією в цій точці. f(x)->Xо ,якщо для будь-якого додатного числа n ( як завгодно великого ) існує число дельта ,що для всіх Х з дельта околу точки Хо виконується нерівність |f(x)|>N або |f(x)|=N
Нескінченно малі і нескінченно великі функції пов’язані між собою:
Теорема
Якщо
α(х) нескінченно мала функція в точці
Хо то функція
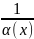 нескінченно велика функція
в цій точці і навпаки .
нескінченно велика функція
в цій точці і навпаки .
Теорема
Для того , щоб функція y=f(x) в точці х0 мала границею число А, необхідно і достатньо , щоб функція f(x)-A була нескінченно малою і цій точці.
56. Порівняння нескінченно малих функцій. Еквівалентні нескінченно малі функції.
Нехай
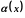 і
і
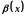 нескінченно малі в точці
нескінченно малі в точці
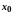 функції. Якщо
функції. Якщо
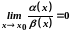 ,
то говорять, що
,
то говорять, що
![]() в околі точки
є нескінченно малою вищого порядку
порівняно з
,
і пишуть
в околі точки
є нескінченно малою вищого порядку
порівняно з
,
і пишуть
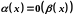 .
.
Якщо
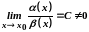 ,
де
,
де
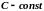 ,
то функції
і
називаються нескінченно малими одного
порядку в околі точки
.
,
то функції
і
називаються нескінченно малими одного
порядку в околі точки
.
Якщо
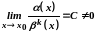 ,
де
,
,
де
,
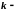 додатне
число, то функція
називається нескінченно малою порядку
додатне
число, то функція
називається нескінченно малою порядку
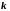 відносно нескінченно малої функції
.
відносно нескінченно малої функції
.
Якщо
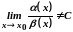 ,
то нескінченно малі функції
і
називаються непорівнянними в околі
точки
.
,
то нескінченно малі функції
і
називаються непорівнянними в околі
точки
.
Якщо
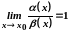 ,
то функції
і
називаються еквівалентними нескінченно
малими в околі точки
.
У цьому випадку пишуть
,
то функції
і
називаються еквівалентними нескінченно
малими в околі точки
.
У цьому випадку пишуть
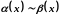 .
.
Теорема.
Якщо
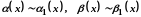 при
при
![]() й існує границя
й існує границя
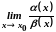 ,
то існує границя
,
то існує границя
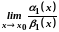 ,
причому
,
причому
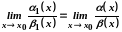 .
.
Доведення.
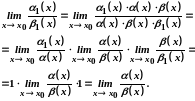
Наведена теорема дає можливість у багатьох випадках спрощувати знаходження границь.
Теорема.
Для того, щоб функції
і
були еквівалентними нескінченно малими
в околі точки
,
необхідно й достатньо, щоб їх різниця
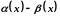 була в околі точки
нескінченно малою вищого порядку по
відношенню до кожної з функцій
та
.
була в околі точки
нескінченно малою вищого порядку по
відношенню до кожної з функцій
та
.
Доведення. Нехай в околі точки . Тоді

Отже, необхідність доведено. Доведемо достатність.
Нехай
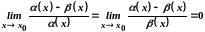 .
.
Звідси маємо
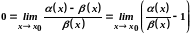 .
.
Таким чином, , тобто в околі точки .
57.
Нехай функція
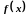 визначена в деякому околі
точки
визначена в деякому околі
точки
![]() .
.
Функція
називається неперервною в точці
,
якщо
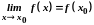 .
.
Наведемо означення неперервності функції, які ґрунтуються на означеннях границі функції за Гейне і за Коші.
Функція
називається неперервною в точці
,
якщо для
будь-якої послідовності
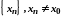 відповідна послідовність
відповідна послідовність
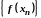 значень збігається до
значень збігається до
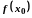 .
.
Функція
називається неперервною в точці
,
якщо для довільного числа
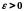 існує число
існує число
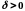 таке, що для всіх
таке, що для всіх
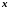 ,
які задовольняють умову
,
які задовольняють умову
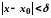 ,
виконується нерівність
,
виконується нерівність
 .
.
Наведені означення рівносильні.
Функція
називається неперервною в точці
справа (зліва), якщо
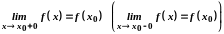 .
.
Отже, функція неперервна в точці , якщо вона неперервна в цій точці як справа, так і зліва.
Покажемо,
що неперервна функція характеризується
тим, що нескінченно малому приростові
аргументу
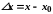 відповідає нескінченно малий приріст
функції
відповідає нескінченно малий приріст
функції
 .
.
Дійсно,
умову
 можна записати як
можна записати як
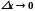 .
Тоді
.
Тоді
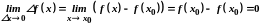 .
.
Отже, можна дати наступне означення неперервності функції в точці . Функція називається неперервною в точці , якщо нескінченно малому приростові аргументу в цій точці відповідає нескінченно малий приріст функції.
Уведене
поняття неперервності функції є локальною
(місцевою) властивістю. Якщо функція
неперервна в кожній точці інтервалу
 ,
то говорять, що вона неперервна на
інтервалі
,
то говорять, що вона неперервна на
інтервалі
![]() .
Якщо при цьому в точці
.
Якщо при цьому в точці
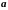 функція неперервна справа, а в точці
функція неперервна справа, а в точці
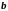 –
неперервна зліва, то говорять, що функція
неперервна на відрізку
–
неперервна зліва, то говорять, що функція
неперервна на відрізку
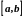 .
.
Зауважимо, що термін неперервної кривої походить із поняття неперервної функції. Графіком неперервної на функції є неперервна крива ("суцільна крива").
58.
Неперервність складеної функції
Теорема
(про неперервність складеної функції).
Якщо функція
неперервна в точці
,
а функція
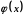 неперервна в точці
неперервна в точці
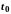 ,
причому
,
причому
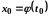 ,
то складена функція
,
то складена функція
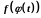 неперервна, як функція від
неперервна, як функція від
 ,
у точці
.
,
у точці
.
Доведення.
Нехай задано довільне число
.
Тоді за неперервністю функції
у точці
знайдеться число
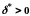 таке, що
для всіх
,
які задовольняють умову
таке, що
для всіх
,
які задовольняють умову
 .
.
Для
числа
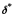 за неперервністю функції
за неперервністю функції
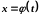 у точці
знайдеться число
таке, що
у точці
знайдеться число
таке, що
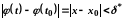 для всіх
,
які задовольняють умову
для всіх
,
які задовольняють умову
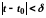 .
.
Отже,
для довільного числа
знайдеться число
таке, що з умови
випливає нерівність
 ,
а це означає, що функція
неперервна в точці
.
,
а це означає, що функція
неперервна в точці
.
Можна довести, що всі елементарні функції в області їх визначення неперервні.
Звернемо увагу на те, що з означення неперервності функції у точці випливає
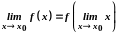 .
.
59.
Точки розриву функції та їх класифікація
Точка називається точкою розриву функції , якщо функція у точці не є неперервною.
Точки розриву класифікують наступним чином.
