4.5. Границя числової послідовності.

Означення 6. Будь-який впорядкований (занумерований) дискретний набір чисел називають числовою послідовністю: 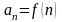, , 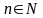тобто послідовність – функція натурального аргументу[14].

Означення 7. Число А називається границею числової послідовності {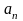 }, пишуть 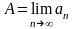, якщо для будь-якого ε>0 знайдеться таке натуральне N, що для всіх n>N виконається умова 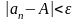. Геометрично це означає, що всі наступні після 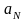елементи послідовності з номерами 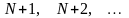обов′язково попадуть в ε-окіл точки А числової прямої

Приклад 13. Довести за означенням, що границею послідовності 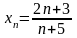є число а=2.

Доведення. Задамо довільне число 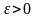, тоді

.

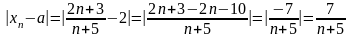З рівності 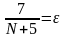знаходимо, що 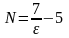. Тоді для всіх n>N нерівність 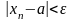виконається £.

Означення 8. Послідовність називається збіжною, якщо вона має границю (скінченну). Послідовність, яка не має границі, називається розбіжною.

Загальні властивості збіжних послідовностей.

Теорема 1: Єдиність границі послідовності. Якщо послідовність має границю, то вона єдина.

Теорема 2: Необхідна умова збіжності послідовності. Якщо послідовність збіжна, то вона обмежена.

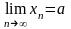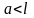
Теорема 3: Якщо і 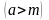, то існує такий номер 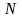, що при всіх 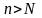виконується нерівність .

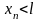
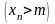Теорема 4: Границя сталої величини дорівнює цій сталій, тобто .

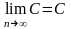Теорема 5: Граничний перехід у нерівності. Якщо для будь-якого n виконується нерівність 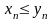і 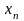, 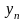- збіжні, то .

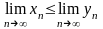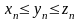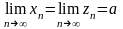Теорема 6: Про границю проміжної послідовності. Якщо для будь-якого n і , то .

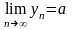Теорема 7. (Вейєрштрасса): Про границю монотонної й обмеженої послідовності:

1) якщо монотонно зростаюча послідовність обмежена згори, то вона збіжна;

2) якщо монотонно спадна послідовність обмежена знизу, то вона збіжна.

Безмежно мала величина та її властивості

Означення 9. Послідовність 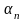називається безмежно малою величиною, якщо 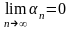і безмежно великою, якщо .

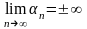Розглянемо деякі властивості таких послідовностей.

Теорема 8. Зв’язок між б.в. і б.м.

1. Якщо - безмежно мала (б.м.) і 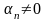, то обернена їй послідовність 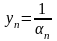буде безмежно великою (б.в.), і навпаки.

2. Якщо - б.в., то обернена їй послідовність 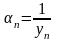- б.м.

Теорема 9. Сума двох б.м. є б.м.

Наслідок. Алгебраїчна сума скінченого числа б.м. є б.м.

Теорема 10. Добуток обмеженої величини на б.м. є б.м.

Теорема 11. Добуток двох б.м. є б.м.

Наслідок. Добуток скінченого числа б.м. є б.м.

Теорема 12. Для існування границі а послідовності необхідно і достатньо, щоб послідовність 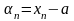була б.м.

Наслідок. Якщо , то 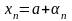, де - б.м.

4.6. Границя функції. Теореми про границі. Ліва та права границі.

Означення 10. Число А називають границею функції y=f(x), тобто , якщо для будь-якого ε>0 знайдеться таке δ>0, що як тільки її аргументи х попадають у δ-окіл точки х₀, так одразу відповідні у=f(x) попадають в ε-окіл точки А. Іншими словами, при виконанні умови 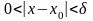обов′язково виконується нерівність 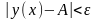[18].

При цьому кажуть, що функція “прямує” до А за умови, що її аргументи х наближаються все ближче до х₀. Важливо, що сама функція в точці х₀ може бути і не заданою. Вона лише “прямує” (надалі лапки ставити не будемо) до числа .

Означення 11. Число В називають границею функції y=f(x), коли , тобто , якщо для будь-якого ε>0 існує число 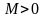таке, що з нерівності 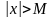випливає нерівність .

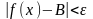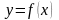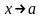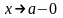Розглянемо односторонні границі для функції , тобто коли з одного певного боку. При цьому домовимось, що позначення означає наближення зліва, а позначення 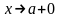- відповідно справа.

Означення 12. Правостороння границя функції:

.

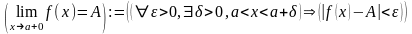Означення 13. Лівостороння границя функції:

.

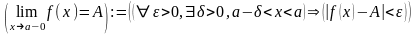Теорема 13. Для існування 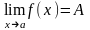необхідно і достатньо, щоб виконувалась умова .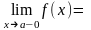

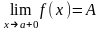Приклад 18. Довести, що 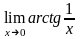не існує.

Розглянемо односторонні границі:

а) ліворуч = ;

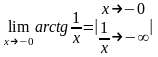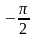б) праворуч = .

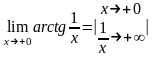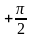Отже, не існує, бо односторонні границі хоча й існують, але не рівні між собою.

Приклади.

1) .

2) .

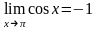3) 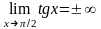(безмежно віддалена точка).

В останньому прикладі функція при π/2=90˚ не існує, однак можна однозначно сказати, куди функція прямує, якщо попередньо домовитись, з якого боку підходити до точки х₀=π/2 – зліва чи справа. Відповідно говорять про ліву границю (пишуть 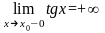), або про праву границю (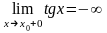 ). Малі добавки вказують таким своєрідним чином, з якого боку здійснюється підхід.

Теореми (про границі функції). Якщ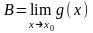о , , то ; ; .

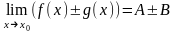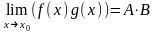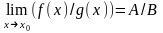В останньому випадку має виконуватись умова В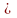 0.

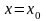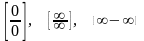Дійсно, якщо окремі доданки-функції або множники-функції якогось виразу прямують до одного і того ж х₀, то і відповідна комбінація границь цих функцій має їх там “чекати”. Границю функції можна обчислювати прямою підстановкою , однак при цьому доволі часто виникають так звані невизначеності. Розглянемо деякі загальні рекомендації щодо дослідження таких невизначених виразів типу , обмежуючись поки що лише алгебраїчними функціями.

Відповідь: .