
- •3.Абсолютна величина числа
- •4.Межі числових множин
- •5. Множина комплексних чисел
- •6.Геометрична інтерпретація комплексних чисел
- •13. Системи визначника n-го порядку. Властивості визначників
- •14.Системи лінійних неоднорідних рівнянь. Роз’язання систем лінійних неоднорідних методом Крамера
- •15. Лінійні простори
- •16. Евклідові простори. Ортогоналізація в евклідовому просторі
- •17. Характеристичні ( власні) числа та власні вектори матриці
- •18. Квадратичні форми
- •4.5. Границя числової послідовності.
- •Загальні властивості збіжних послідовностей.
- •Безмежно мала величина та її властивості
- •4.6. Границя функції. Теореми про границі. Ліва та права границі.
- •4 .7. Дві визначні границі.
- •50.Число e
- •51.Границя функцій
- •52.Теореми границі функції
- •53.Перша визначна границя функції:
- •54. Друга визначна границя функції:
- •55.Нескінченно малі і великі функції
- •Розриви першого роду. Якщо в точці функція має скінченну ліву й скінченну праву границю і вони рівні між собою, тобто
- •Але відмінні від значення функції в точці або значення не існує, то точка називається точкою усувного розриву функції
- •60. Операції над неперервними функціями
- •62. Перша і друга теореми Вейєрштрасса.
- •63. Поняття рівномірної неперервності. Теорема Кантора.
- •64. Поняття оберненої функції. Теорема про неперервність оберненої функції.
- •65. Поняття похідної, геометричний зміст похідної. Права і ліва похідні.
- •6 6. Поняття диференційовності функції в точці. Зв'язок між диференційовністю та неперервністю функції.
- •67. Похідна суми, частки, добутку функцій.
- •70 Таблиця похідних основних елементарних функцій
- •Диференціал функції
- •86.Асимптоти кривої. Загальна схема дослідження функції.
- •87.Загальний план дослідження функції та побудови її графіків.
- •88, 89. Функції двох змінних
- •90. Неперевність функції багатьох змінних
- •91. Основні властивості непервності функції
- •101.Формула тейлора для функції багатьох змінних
- •102.Поняття неявної функції. Теорема існування і диференційованості неявної функції
- •103.Екстремум функції двох та багатьох змінних. Необхідні і достатні умови екстремуму
- •104.Екстремуми функцій багатьох змінних. Умовний екстремум.
15. Лінійні простори
Означення. Множину L наз. Лінійним простором, якщо
Кожним двом елементам a I b множиниL ставиться у відповідність третій елемент цієї множини, який називається сумою і позначається a+b.
Кожному елементу a множ. L і довільному числу
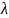 ставиться у відповідність елемент з
цієї множини, який наз. добутком елемента
а на число
ш позначається
ставиться у відповідність елемент з
цієї множини, який наз. добутком елемента
а на число
ш позначається
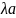 .
.Для вільних елементів a,b,c множ L і для довільних чисел
 справдяться аксіоми:
справдяться аксіоми:
a+b = b + a - операція «+» комутативна
(a+b)+c=a+(b+c) – операція «+» асоціативна
Існує нульовий елемент 0 множ L такий, що для довільного елемента a множ L виконується рівність a + 0 = 0 + a = a
Для кожного елемента а множ L існує протилежний елемент –а з множини L такий, що а + (-а) = (-а) +а = 0
(
 )а
=
)а
=
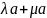
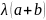 =
=
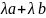
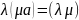 a
a
16. Евклідові простори. Ортогоналізація в евклідовому просторі
Точковий
простір називають m-вимірним
евклідовим простором, якщо відстань
між будь-якими 2 його точками M1(c
; x2(1) ; ….; xm(1)
) та M2(x1(2)
; x2(2) ; ….; xm(2)
) можна обчислити за формулою
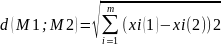 .
Евклідів m-вимірний простір
позначають символом Rm.
.
Евклідів m-вимірний простір
позначають символом Rm.
Відстань між
2 точками можна визначити за формулою
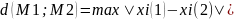 (1<=i<=m)
(1<=i<=m)
d(M1,M2)=
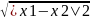 = |x1-x2|, де
х1,х2 – координати т. М1 і М2, збігається
з числовою прямою, простір R2
з метрикою d(M1,M2)=
= |x1-x2|, де
х1,х2 – координати т. М1 і М2, збігається
з числовою прямою, простір R2
з метрикою d(M1,M2)=
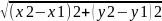 ,
де М1(х1, у1) і М2(х2, у2) з координатною
площиною, а простір R3
з метрикою d(M1,M2)=
,
де М1(х1, у1) і М2(х2, у2) з координатною
площиною, а простір R3
з метрикою d(M1,M2)=
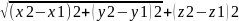 .
.
Означення Множину Е m – вимірного евклідового простору наз. лінійно залежною. Якщо довільні 2 точки цієї множини можна з’єднати неперервною кривою, яка цілком міститься у множині Е.
Означення
Множину Е усіх точок М евклідового
простору Rm,
координати х1, х2,…, хm яких
задовольняють нерівність
 наз. відкритою m-вимірнрю
кулею радіуса R з центром
у точці M0(x1(0);
x2(0);…;xm(0).
d(M;M0)<R
наз. відкритою m-вимірнрю
кулею радіуса R з центром
у точці M0(x1(0);
x2(0);…;xm(0).
d(M;M0)<R
Означення
Кожну відкриту m-вимірну
кулю радіуса
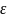 > 0 з центром в точці М0 наз.
> 0 з центром в точці М0 наз.
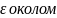 точки М0 і поз. U
(M0).
точки М0 і поз. U
(M0).
Означення
Відкриту m-вимірну кулю
радіуса
> 0 з центром в точці М0, з якої видалена
сама точка М0, наз. проколеним
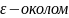 точки М0 і позначають U
(M0).
точки М0 і позначають U
(M0).
Означення Точку М наз. Внутрішньою точкою множини Е, якщо існує деякий окіл U(M) цієї точки, якмй містить точки множини Е.
Одначення Множину, яка складається лише з внутрішніх точок, наз. відкритою множиною.
Означення Лінійно зв’язну і відкриту множину наз. відкритою областю або просто областю.
Означення Точку М наз. межею точкою множини Е, якщо будь – який окіл U(M) цієї точки містить як точки, що належать множині Е.
17. Характеристичні ( власні) числа та власні вектори матриці
Означення
Число
наз.
власним числом(значенням) оператора А,
а ненульовий вектор х – власним вектором,
що відповідає власному значенню
,
якщо виконується рівність Ах =
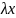 .
.
О значення
Множину власних значень оператора А
наз. спектром оператора .
значення
Множину власних значень оператора А
наз. спектром оператора .
Дана
с-ма має ненульовий розвязок тоді і
тільки тоді, коли визначник матриці
с-ми рівний нулеві(rang(
18. Квадратичні форми
К вадратичною
формою наз. числову функцію Q(x,x)
= Q(x1,x2,…,xn)
векторного аргументу х , яка має вигляд
Q(x,x)
=
вадратичною
формою наз. числову функцію Q(x,x)
= Q(x1,x2,…,xn)
векторного аргументу х , яка має вигляд
Q(x,x)
=
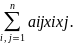
Cиметричну матрицю
наз.
Квадратною формою Q(x,x).
Кожній симетричній матриці А відп.
Квадратна форма Q(x,x)
=
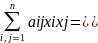 ХАХТ,
де Х = (х1, х2,…,хn).
ХАХТ,
де Х = (х1, х2,…,хn).
Зведення
квадратичної форми до канонічного
вигляду. Квадратична форма має
канонічний вигляд, якщо аij
= 0, i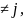 Q(x,x)
=
Q(x,x)
=
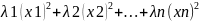 .
Коєфіцієнти
.
Коєфіцієнти
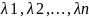 – канонічні коефіцієнти
– канонічні коефіцієнти
Теорема
(критерій Сильвестра). Для того, щоб
квадратична форма Q(x,x)
була додатно визначена, необхідно і
достатньо, щоб виконувались нерівності
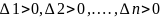 . Для того, щоб квадратна форма була
від’ємно визначена, необхідно і
достатньо, щоб знаки кутових мінорів
чергувались, причому
. Для того, щоб квадратна форма була
від’ємно визначена, необхідно і
достатньо, щоб знаки кутових мінорів
чергувались, причому
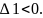


Вектор – напрямлений відрізок певної довжини, у якого один кінець вважається
початком вектора, а інший – кінцем вектора.
Властивості лінійних операцій над векторами:


Означення. Базисом системи векторів a1, a2,… am є Rn називається її підсистема ai1,ai2,..,aik така, що
Підсистема ai1,ai2,..,aik лінійно незалежна;
Всі вектори системи a1, a2,… am лінійно виражаються через ai1,ai2,..,aik.
Означення. Базисом простору Rn називається система векторів a1, a2,… an є Rn така, що
система a1, a2,… an лінійно незалежна;
Кожний вектор простору Rn лінійно виражається через a1, a2,… an. .
Покажемо існування базису простору
Rn.
Візьмемо в просторі таку систему
векторів:
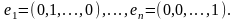
Перевіримо виконання умови базису для даної системи.
Лінійна незалежність. Беремо лінійну комбінацію
α1e1+ α2e2+…+ αnen =,
тоді для координат векторів виконується
(α1, α2,…, αn)=(0,0,…,0).
Звідси α1= α2=…=αn=0, лінійна коомбінація тривіальна і система лінійно незалежна.
2. Будь-який вектор простору лінійно
виражається через e1,e2,…,en
. Беремо довільний вектор
x=(β1,
β2,…, βn). Тоді
x= β1e1+
β2e2+…+ βnen
.

Отже, умови базису виконуються. Базис e1,e2,…,en називається стандартним базисом простору Rn.
Ми переконалися в тому, що в просторі Rn існує лінійно незалежна система, яка складається з n векторів. Припустимо, що в просторі існують лінійно незалежні системи з числом векторів, більшим n . Візьмемо одну таку систему a1, a2,… am є Rn , m>n. За доведеним, вектори e1,e2,…,en утворюють базис простору, тому всі вектори простору лінійно виражаються через e1,e2,…,en. Зокрема, це означає, що всі вектори системи a1, a2,… am лінійно виражаються через e1,e2,…,en. Але, оскільки m>n, то за лемою про дві системи, вектори a1, a2,… am лінійно залежні, що суперечить припущенню. Отже, ми довели наступне твердження.
В просторі Rn будь-яка система з m векторів m>n лінійно залежна.












26-27.

Умова паралельності прямої і площини:
Am+Bn+Cp=0.
Умова перпендикулярності прямої і площини:
A/m=B/n=C/p.
2˚.Точка перетину прямої і площини.Для
знаходження точки перетинку прямої

підставити в рівняння площини Ax+By+Cz+D=0 і знайти tc а потім координати xc, yc, zc(c-має бути знизу як індекс).Координати точки перетину прямої і площини називаються слідом.
3˚.Умова розміщення двох прямих в одній площині
Дві прямі х-хʹₒ/m = y-yʹₒ/n = z-zʹₒ/p і x-xʺₒ/m = y-yʺₒ/n = z-zʺₒ/p лежать в одній площині ,якщо виконується співвідношення
│ хʹₒ-xʺₒ yʹₒ-yʺₒ zʹₒ-zʺₒ │
│ │
│ m1 n1 p1 │ =0.
│ │
│ m2 n2 p2 │
28.Еліпсом називається геометричне місце точок,сума відстаней від кожної з яких до двох заданих точок F1 i F2(фокусів) є стала величина 2а більша ,ніж | F1 F2|.
Канонічне рівняння еліпса:
x²/a²+y²/b²=1
Еліпс,заданий канонічним рівняння ,симетричний щодо осей координат
Параметри а і b називаються півосями еліпса(велика і мала відповідно)
Якщо а>b то фокуси F1 і F2 розміщені на осі Ох на відстані с=√a²-b²
Відношення фокусної відстані еліпса до його великої піввісі називають ексцентриситетом(с/а= ε<1)
Відстані від точки селіпса до його фокусів (фокальні радіуси) визначають за формулами
r1=ɑ - εx r2= ɑ + εx
29.Гіперболою називається геометричне місце точок ,різниця відстаней від кожної з яких до двох заданих точок F1 i F2 (фокусів) є сталою величиною 2а(0<2a<| F1 F2|)
Канонічне рівняння гіперболи
x²/a²- y²/b² =1.
Гіпербола що задана канонічним рівнянням симетрична відносно осей координат.Вона перетинає Ох в точках А(а;0) і A1(-a;0) – вершинах параболи і не перетинає вісь Оу.Параметр а називається дійсною піввіссю,b-уявною.
Параметр с=√a²+b² є відстанню від фокуса до центра.
с/а= ε>1 називають ексцентриситетом.Прямі у=±b/a називаються асимптотами гіперболи.
Відстань від точки M(x;y) гіперболи до її фокусів (фокальні радус-вектори) визначають за формулами
r1= | εx-a| r2= | εx+a|
Гіпербола в якої a=b називається рівносторонньою її рівняння x²-y²=a² a рівняння асимптот у=±х
Гіперболи x²/a²- y²/b² =1 і y²/b²- x²/a²=1 називаються спряженими.
30.Параболою називається геометричне місце точок однаково віддалених від заданої точки (фокуса)і заданої прямої (директриси)
Канонічне рівняння параболи
y²=2px
Парабола y²=2px має фокус F(p/2;0) і директрису x=-p/2;фокальний радіус-вектор точки M(x;y) на ній r=x+p/2.
40.





42.




41.





43.
Поняття числової послідовності
Нехай кожному натуральному числу n відповідає по деякому правилу число an. Кажуть, що задана числова послідовність
a1,a2,...,an,...
Числа a1,a2,... називаються членами послідовності; an – n-й або загальний член послідовності. Саму послідовність позначають так: (an).
Таким чином, числовою послідовністю (an) (або, коротше, послідовністю) називається функція, задана на множині натуральних чисел.
Наприклад, якщо відомо, що
an=n2
при будь-якому n, то a1=1,a2=4,a3=9 і т.д.
Деякі способи задання послідовності
1) Аналітичний спосіб задання послідовності. Задати послідовність аналітично – це означає вказати формулу, яка дозволяє по номеру члена послідовності однозначно визначити цей член. Формула, яка дозволяє обчислити будь-який член послідовності по його номері, називаєтьсяформулою загального члена числової послідовності.
Наприклад, формула загального члена
an=(−1)n−1n,
задає наступну числову послідовність
1,−12,13,−14,15,...
2) Інколи послідовність задається рекурентною формулою, яка дозволяє знаходити члени послідовності по відомим попереднім членам. Наприклад, розглянемо послідовність (an), перший член якої рівний 1, другий 2, а кожний член, починаючи з третього, рівний сумі двох попередніх членів:
a1=1,a2=2,an+2=an+an+1.
Тоді
a3=1+2=3,
a4=2+3=5,
a5=3+5=8
і т.д. Значить, послідовність (an) задана.
3) Послідовність може бути також задана описом способу отримання її членів. Так, наприклад, говорять, що послідовність
3,1;3,14;3,141;3,1415;...
Утворена із приблизних значень числа π з недостачею з точністю до
0,1;0,01;0,001;0,0001;...
і т.д. В подібних випадках, як правило, не можна вказати ні формули загального члена послідовності, ні рекурентного способу обчислення її членів.
Монотонні послідовності
Послідовність (an) називається зростаючою, якщо кожен її член, починаючи з другого, більший за попередній, тобто якщо для будь-якого натурального n виконується нерівність
an+1>an.
Послідовність (an) називається спадною, якщо кожен її член, починаючи з другого, менший за попередній, тобто якщо для будь-якого натурального n виконується нерівність
an+1<an.
Послідовність (an) називається неспадною, якщо кожен її член, починаючи з другого, не менший за попередній, тобто якщо для будь-якого натурального n виконується нерівність
an+1≥an.
Послідовність (an) називається незростаючою, якщо кожен її член, починаючи з другого, не більший за попередній, тобто якщо для будь-якого натурального n виконується нерівність
an+1≤an.
Зростаючі, спадні, неспадні та незростаючі послідовності називаються монотонними послідовностями.
Зростаючі та спадаючі послідовності називають строго монотонними.
Нижня та верхня межа
Послідовність (an) називається обмеженою знизу, якщо існує таке число A, що для кожного члена послідовності справджується нерівність an>A. Число A називається нижньою межею послідовності (an).
Послідовність (an) називається обмеженою зверху, якщо існує таке число B, що для кожного члена послідовності справджується нерівність an<B. Число B називається верхньою межею послідовності (an).
Границя послідовності
Число a називається границею послідовності (an) і записують
limn→∞an=a
якщо для будь-якого додатного числа ε знайдеться номер N(ε) члена послідовності, починаючи з якого буде виконуватися нерівність
|an−a|<ε (1)
Примітка. lim — це скорочення латинського слова «limes», яке означає «границя».
Числову послідовність називають збіжною, якщо вона має границю. Послідовність, яка не має границі, називають розбіжною.
Нерівність (1) також може бути записана у вигляді:
a−ε<an<a+ε.
Інтервал (a−ε;a+ε) називають околом точки a.
Геометричний зміст границі послідовності
Якщо a — границя послідовності (an), то який би окіл точки a ми не вибрали, члени послідовності, починаючи з деякого номера N, будуть зображуватись точками, які лежать в цьому околі:

Основні властивості границь
Якщо послідовності (an) і (bn) мають границі, то:
limn→∞(an±bn)=limn→∞an±limn→∞bn
limn→∞(an⋅bn)=limn→∞an⋅limn→∞bn
limn→∞anbn=limn→∞anlimn→∞bn
38-39.









