13. Системи визначника n-го порядку. Властивості визначників

Властивості визначників.

1. Рівноправність рядків і стовпців визначника. При транспонуванні визначник матриця не змінюється detA = detA^-.

Наступні властивості будуть сформульовані лише для рядів, проте в силу 1 властивості вони будуть рівними і для стовпців.

2. Від перестановки 2-х визначників місцями його абсолютна величина залишається без змін, а знак змінюється на протилежний

=

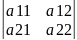Наслідок. Визначник який має 2 однакових рядки рівний 0.

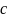= = 0

= = - = -

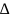3. Спільний множник елемента будь – якого рядка визначника можна винести за знак визначника

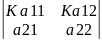= K

Доведення.

Ka11*a22-Kа12*а21= К(а11*а22-а12*а21)= K

Наслідок 1. Визначник який містить нульовий рядок 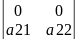= 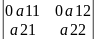0

= =0*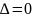

Наслідок 2. Визначник який має пропорційні рядки = 0

= K =К *0=0

4. Якщо всі елементи деякого рядка визначника є сумою 2-х доданків, то визначник можна представити у вигляді суми 2-х відповідних визначників.

=

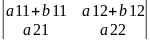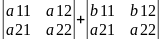
Наслідок. Величина визначника не зміниться, якщо до елементів визначника + елемент паралельного рядка визначника помножити на одне і те число.

=

= = =

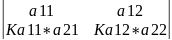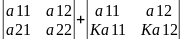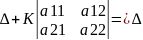
Визначник n-го порядку

Означення. Визначноком n-го порядку називають число, яке ставлять у відповідність квадратній матриці n-го порядку, яке позначається і обчислюється за правилом

а11 а12 … а 1n

a21 a22 … a2n

……………………… =

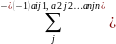
am1 am2 … amn

Для визначника n-го порядку є вірними властивості властивості сформульовані для визначника 3 порядку.

Означення. Мінором Mij елементу aij визначника n-го порядку називають визначник (n – 1) порядку, який отриманий із визначника шляхом викреслювання I рядка і j стопця на перетині яких розміщений елемент aij.

Означення. Алгебраїчним доповненням елемента Aijназивається число Aij = (-1)^{I + 1}Mij

Визначники крім властивостей 1-4 володіють наступними властивостями:

5. Сума добутків елементів будь – якого рядка визначника на їхні алгебраїчні доповнення рівна величині визначника.

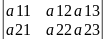= =а11*А11+а12*А12+а13*А13

а31 а32 а 33

Aij= (-1)^{I + 1}Mij

6. Сума добутків елементів будь – якого рядка визначника на алгебраїчне доповнення елемента паралельного рядка визначника = 0

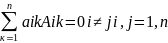
7. Det(A*B) = detA * detB

Де А, В – квадратна матриця

Зауваження1. Визначник матриці рівний добутку елементів головної діагоналі

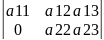=а11*а22….*anm

0 0 а 33

Зауваження2. Визначник діагональної матиці рівний добутку елементів головної діагоналі.

14.Системи лінійних неоднорідних рівнянь. Роз’язання систем лінійних неоднорідних методом Крамера

Таку систему називають однорідною. Лінійна однорідна система має нульовий розв’язок x=y=z=0. Cистемою лінійних неоднорідних рівнянь називають матрицю, визначник якої відмінний від 0.

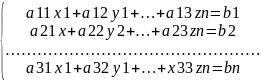
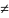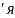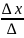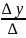У цьому випадку система матриці А є квадратною матрицею порядку n. Якщо матриця А невироджена , тобто det A 0. Нехай система має ненульовий розв зок (x1, y1 z1). Припустимо, що , тоді цей розв’язок шукають за формулою Крамера x1 = , y1 = , z1=

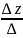
Правило Крамера застосовують для розв’язання систем з квадратною матрицею А( тобто m=n) . Для системи лінійних неоднорідних рівнянь розміром n*n шукаємо визначник матриці, а також допоміжний визначник за формулою :

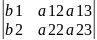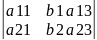х = y = х =

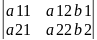
b1 а32 а 33 a31 b3 а33 a31 a32 b3

Послідовно помножим систему рівнянь на алгебраїчні доповнення А11, А12, А13 на а11, а12, а13 відповідно. В результаті отримаємо ( a11A11 + a21A21 + a31A31)x + (a12A12 + a22A22 + a32A32)y + (a31A31 + a32A32 + a33A33)z = b1A11 + b2A21 +b3A31.

Звідси, x1 = , y1 = , z1=

Якщо то система має єдиний розв’язок.