1. Поняття висловлення. Логічні операції та основні закони алгебри висловлень

Ознаяення.Висловлення — це розповідне речення, про яке є сенс

говорити, шо воно істинне (позначатимемо 1) або хибне (позначатимемо через О). Висловлення зручно позначати літерами латинського алфавіту

Під час побудови висловлень будемо використовувати такі закони: 1) кожне висловлення є істинним або хибним (закон виключення третього);

2) жодне висловлення не може бути одночасно істинним і хибним (закон суперечноcті);

3) речення, на яке не можна однозначно дати відповідь, істинне воно чи хибне не є висловленням.

В математичній логіці є п'ять логічних операцій: кон'юнкція, диз'юнкція, імплікація, заперечення та еквiвалентнiсть. 3 простих висловлень за допомогою вказаних логічних операцій утворюють нові висловлення, які називають складними.

Означення. Кон 'юнкцією висловлень р та q називають таке висловлення, яке є істинне тоді, коли висловлення р та q істинні одночасно.

Кон'юнкцію позначають р^q і читають "р та q", "р і q".

Означення. Диз'юнкцією висловлень р та q називають таке висловлення,

яке є істине тоді, коли хоча б одне э висловлень р або q є істинним.

Диз'юнкцію позначають р ∨ д і читають "р або q".

Означення. Запереченням висловлення р називають висловленни, яке є

хибним, якщо висловлення р істинне, та істивним, якшо р — хибне.

Заперечення позначають або ¬ р і читають "не р "

Означення. імплікацією висловлень р та q називають таке висловлення,

яке є хибне тоді, коли висловлення р є істинним, а висловленни q є -хибиим, у всіх інших випадках це висловленна є істивне.

Імплікацію р⇒ q або р→ q читають "з р випливає q " "р зумовлює q ", "якщо р, то q".

У цьому випадку р називають засновком, q — наслідком або висновком.

Оэначення. Еквівалвнтнісiтю висловлень р та q називають висловлення, яке істинне тоді, коли висловлення р та q є істинними або хибними одночасно.

Еквівалентність позначають р ⇔ q і читають "р еквівалентне q"

Означвння. Висловлення р та q називають рівносильними, якщо

висловлення р ⇔ q істинне.

Нові висловлення можна утворювати з простих висловлень за допомогою кількох логічних операцій, причому кожну з операцій можна застосовувати декілька разів. В результаті отримаємо складне висловлення. Порядок, в якому повинні виконуватися операції, вказують за допомогою дужок. Наприклад, запис (р⇒q) ∨ r означає, що спочатку виконують імплікацію у дужках, а потім -диз'юнкцію.

Щоб спростити запис складного висловлення часто опускають дужки. Прийнято, що якщо відсутні дужки, то логічні операції виконують в наступному порядку:

¬,^,∨,⇒,⇔

Закони алгебри висловлень:

1. Комутативність конюнкції p^q = q^p

2. Комутативність дизюнкції p\/q = q\/p

3. Асоціативність конюнкції (p^q)^r= p^(q^r)

4. Асоціативність дтзюнкції (p\/q)\/r= p\/(q\/r)

5. Перший дистрибутивний закон p^(q\/r)=(p^q)\/(p^r)

6. Другий дистрибутивний закон p\/(q^r)= (p\/q)^(p\/r)

7. Закон Деморгана. ne(p^q)=ne(p)\/ne(q)

8. Заперечення ne ne p =p

Закон Іденпотентності p\/p=p, p^p=р

Важливу роль у роль відіграють тотожно істинні та тотожно хибні вислолення.

Означення. Толожно істиннні висловлення істинні завжди, незалежно від того, істинні чи хибні складові цього висловлепня.

Тотожно істннні висловлення позначатимемо буквою “і”, часто їх називають тавтологіями. Наприклад, висловлення р ∨ ¬р є тотожно істинним .

Означення. Толожно хибні висловлення хибні завжди, незалежно від того, істинні чи хибні складові цього висловленыя.

Тотожно хибні висловлення позначатимемо буквою “f“.Наприклад, висловлення р ^ ¬р є тотожно хибним, тобто р ^ ¬р р = f.

Для тотожно істинних і тотожно хибних висловлень при довільному р вірні такі рівності:

2.Аксіома множини дійсних чисел

Означення. Множину R називають множиною дійсних чисел, а її елементи дійсними числами, якщо виконується сукупність умов, яку називають аксіоматикою дійсних чисел.

І. Аксіоми додавання

На декартовому добутку множин R х R визначено відображення

R х R →R, що називають операцією додавання, яке в кожній впорядкованій парі

елементів (х;у) ставить у відповідність елементи х+у множини R, який

називають сумою. ІЦодо операції додавання вірними є такі властивості:

1')існує нейтральний елемент О множини R, який у випадку операцій додавання називають нулем, такий що для будь-якого елемента х множини R виконується рівність х+0 = 0+х = х;

2') для будь-якого елемента к множини R існує елемент “-х” який називають протилежним елементом до х, причому х+ (-х) = ( -х)+ х = 0;

3') операція додавання є асоиіативною, тобто для будь-яких елеменззв х, у, =

множини R виконується рівність (х+ у) + z = х+ (у+ z);

4') операція додавання комутативна, тобго для будь-яких елементів х,у

множини R виконується рівність х+у = у+ х.

II. Аксіоми множення

На декартовому добутку множин R х R визначено відображення ; R х R →R, що називають операиією множення, яке кожній впорядкованій парі елементів (х; у) ставить у відповідність елемент х. у множини R, який називають добутком.

Щодо операції множення вірними є такі властивості:

1")існує нейтральним елемент 1 множини R, який у випадку множення

називають одиницею, такий що для будь-якого елементу х множини R

виконується рівність х*1=1*х = х;

2")для будь-якого ненульового елементу множини R існує елемент х^-1, який

називають оберненим, такий, що виконується рівність х* х^-1=. х^-1 *х =1;

3 ") операція множення асоціативна, тобто для будь-яких ненульових елементів

х,у,z множини R виконується рівність (х*у) *z= х*(у*z);

4")операція множення комутативна, |тобто для будь-яких ненульових

елементів х, у множини R виконуєгься рівність х* у = у *х.

Означення. Якщо на деякій множині Х визначена операція, що

задовольняє аксіоми 1') — 3'), то говорять що на множині Х задано

структуру групи або множина Х є групою. Якщо визначена операція є операцією додавання, то групу Х називають адитивною.

Означення. Якщо на деякій множині Х визначена операція, що

задовольняє аксіоми 1') — 4') то множину х називають комутативною групою.

І — ІІ. Зв'язок між множенням та додаванням

Операція множення є дистрибутивною стосовно операції додавання, тобто для будь-якик ненульових елементів х, у, i множини R виконується рівність (х+у) *z =х *z+ у*z;.

Означення. Якщо на деякій множині Х задані дві операщї: додавання та множення. що задовольняють аксіоми 1') — 4') та 1") — 4") відповідыо, і операція множення є дистрибутивною щодо операції додавання, то множину Х називають понем.

111. Аксіоми порядку

Між елементами множини К задане ві дногиення нерівності р =-<, тобто для елементів множини R визначено, чи виконується відношення х < у, чи ні.

Щодо відношення нерівності < справедливі наступні аксіоми. які називають аксіомами порядку:

Означення. Множину, між елементами якої визначене відношення, шо

задовольняє аксіоми порядку 1)-3), називають лінійно впорядкованою.

Отже, множина дійсних чисел R є лінійно впорядкована відношенням

нервності між її елементами.

3.Абсолютна величина числа

4.Межі числових множин

Означення. Множину Х «R називають обмеженою зверху, якщо існує таке число М з множини дійсних чисел R, що для будь-якого елеметпу х з множини Х виконується відношення х < М . Число М називають верхнього межею множини Х або мажорантою.

Означення. Множину Х ⊂ R називають обмеженою знизу, якщо існує таке число т з множини дійсних чисел R, що для будь-якого елементу х з множина Х виконується відношення х > m.

Число т називають нижньою межею множини Х або мінорантою.

Означення. Множину, обмежену зверху і знизу, називають обмежено множиною.

Означення. Елемент а множини Х ⊂ R називають найбішим або максмальним елементом множини Х, якщо для будь-якого елемента х множини Х виконується відношення х ≤ а.

Означення. Елемент а множини Х ⊂ R називають найменшим або мінімальним елементом множини Х, якщо для будь-якого елемента х множини Х виконується відношення а ≤ х.

Формальний запис означення для максимального і мінімального елементів має наступний вигляд:

Означення. Найменше з чисел, що обмежують множину Х ⊂ R зверху називають точною верхньою межею множини і позначають supX (супремум X).

Означення. Найменше з чисел, що обмежують множину Х ⊂ R знизу називають точною нижньою межею множини і позначають infX (інфімум X).

5. Множина комплексних чисел

Означення. Множиною комплексних чисел С називають множину впорядкованих пар z=(x;y) дійсних чисел x і y, для яких рівність ,суму ,добуток і ототожнення деяких впорядкованих пар визначачають за правилами:

1. Два комплексних числа z₁=(x₁;y₁) і z₂=(x₂; y₂) називають рівними якщо x₁= x₂ і y₂ =y₁;

2. Сумою двох комплексних чисел z₁=(x₁;y₁) і z₂=(x₂; y₂) називають комплексне число z=z₁+z₂=(x₁+x₂;y₁+y₂);

3. Добутком двох комплексних чисел z₁=(x₁;y₁) і z₂=(x₂; y₂) називають комплексне число

z=z₁⋅z₂ =(x₁x₂-y₁y₂; x₁y₂+x₂y₁);

4. Множину комплексних чисел вигляду (x;0), x∈R, отожнюють з множиною дійсних чисел R.

число х називають дійсною частиною комплексного числа z і позначають x=Re z; y називають уявною частиною z і позначають символом y =lm z.

Властивості комплексних чисел

1. Для кожного комплексного числа z існує комплексне число – z таке, що

z+(– z)= – z+z=0.

2. Операція додавання асоціативна: (z₁+z₂)+z₃=z₃+(z₂+z₃).

3. Операція додавання комутативна : z₁ +z₂ =z₂+z₁.

4. Існує комплексне число вигляду z₁=(1,0), яке є нейтральним елементом відносно операції множення, тобто для довільного комплексного числа z існує таке комплексне число z₁ що вірною є рівність z⋅ z₁ =z₁⋅z=z.

5. Для,будь-якого комплексного числа z існує обернене число z₁, тобто для довіньного комлексного числа z виконується рівність z⋅ z₁ =z₁⋅z=1.

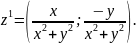
6. Операція множення комплексних чисел асоціативна , тобто вірна рівність

(z₁⋅z₂) ⋅z₃=z₁⋅(z₂⋅z₃)

7. Операція множення є дистрибутивною щодо операції додавання,тобто для довільних комплексних чисел z1,z2,z3 вірна рівність (z1+z2) ⋅z3=z1⋅z3+z2⋅z3

Означення. Різницею комплексних чисел z1 і z2 називають комплексне число z таке, що z₂+z = z₁;

z = z₁+(–z₂)=(x₁-x₂;y₁-y₂);

Означення. Часткою двох комплексних чисел z₁ z₂ називають комплексне число я таке що z₂⋅z=z₁;

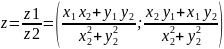
Означення. Комплексне число вигляду z*=(x;-y)=x-iy називають спряженим щодо комплексного числа z=(x,y)=x+iy

z⋅z*=x²+y²