
- •В.М. Игнатович, ш.С. Ройз электрические машины и трансформаторы
- •1. Трансформаторы
- •1.1. Устройство и принцип действия трансформаторов
- •1.2. Основные уравнения трансформатора
- •1.3. Электрическая схема замещения трансформатора
- •1.4. Опыт холостого хода
- •1.5. Опыт короткого замыкания
- •1.6. Векторные диаграммы трансформатора при нагрузке
- •1.7. Внешние характеристики трансформатора
- •1.8. Регулирование напряжения трансформаторов
- •1.9. Потери и кпд трансформатора
- •1.10. Схемы и группы соединений обмоток трансформаторов
- •1.11. Параллельная работа трансформаторов
- •1.12. Несимметричная нагрузка трехфазных трансформаторов
- •Физические условия работы трансформаторов при несимметричной нагрузке
- •1.13. Многообмоточные трансформаторы
- •1.14. Автотрансформаторы
- •1.15. Автотрансформаторы с переменным коэффициентом трансформации
- •1.16. Трансформаторы для дуговой электросварки
- •1.17.Переходные процессы в трансформаторах
- •Включение трансформатора в сеть
- •Внезапное короткое замыкание на клеммах вторичной обмотки трансформатора
- •Лабораторные работы и контрольные вопросы по разделу «трансформаторы»
- •Исследование двухобмоточного трехфазного трансформатора при симметричной нагрузке
- •Исследование двухобмоточных трехфазных трансформаторов при несимметричной нагрузке
- •Группы соединений обмоток трехфазного трансформатора
- •Исследование параллельной работы однофазных трансформаторов
- •2. Асинхронные машины
- •2.1. Устройство асинхронной машины
- •2.2. Трехфазные обмотки машин переменного тока
- •1. Расчет шага обмотки
- •2. Расчет числа пазов на полюс и фазу q (число катушек в катушечной группе)
- •3. Расчет угла сдвига фаз эдс
- •2.2.1. Трехфазные двухслойные обмотки
- •2.2.2. Трехфазные однослойные обмотки
- •2.3. Электродвижущая сила обмоток переменного тока
- •Коэффициент укорочения шага обмотки
- •Коэффициент распределения обмотки
- •Коэффициент скоса пазов
- •Эдс обмотки от высших гармоник поля
- •2.4. Вращающееся магнитное поле
- •2.5. Принцип действия асинхронной машины и режимы работы
- •2.6. Уравнения напряжений асинхронного двигателя
- •2.7. Уравнения мдс и токов асинхронного двигателя
- •2.8. Приведение параметров обмотки ротора, векторная диаграмма и схемы замещения асинхронного двигателя
- •2.9. Энергетические диаграммы активной и реактивной мощностей асинхронной машины
- •2.10. Вращающие моменты асинхронной машины
- •2.11. Способы пуска трехфазных асинхронных двигателей (ад)
- •2.11.1. Способы пуска ад с короткозамкнутым ротором
- •2.11.2. Пуск ад с фазным ротором
- •2.12. Регулирование частоты вращения ад
- •Лабораторные работы и контрольные вопросы по разделу «асинхронные машины»
- •1. Исследование асинхронного двигателя с короткозамкнутым ротором
- •Исследование асинхронного двигателя с фазным ротором
- •Исследование асинхронного двигателя в трехфазном, конденсаторном и однофазном режимах
- •3. Синхронные машины
- •3.1. Устройство и принцип действия синхронной машины
- •3.2. Магнитное поле обмотки возбуждения синхронной машины
- •3.3. Магнитное поле и параметры обмотки якоря
- •3.3.1. Продольная и поперечная реакции якоря
- •3.4. Магнитные поля и эдс продольной и поперечной реакции якоря
- •3.5. Векторные диаграммы напряжений синхронных генераторов
- •3.6. Характеристики синхронного генератора
- •3.6.1. Характеристика холостого хода при
- •3.6.2. Характеристика трехфазного короткого замыкания при
- •3.6.3. Отношение короткого замыкания
- •3.6.4. Внешние характеристики
- •3.6.5. Регулировочные характеристики
- •3.6.6. Индукционная нагрузочная характеристика
- •3.7. Диаграмма Потье
- •3.8. Параллельная работа синхронных генераторов
- •3.8.1. Условия включения генератора на параллельную работу
- •3.8.2. Синхронные режимы параллельной работы синхронных машин
- •3.8.3. Угловые характеристики активной мощности синхронных машин
- •3.8.4. Синхронизирующая мощность (синхронизирующий момент) и статическая перегружаемость синхронных машин
- •3.8.5. Работа синхронной машины при постоянной активной мощности и переменном возбуждении
- •3.9. Элементы теории переходных процессов синхронных машин
- •3.9.1. Гашение магнитного поля
- •3.9.2. Физическая картина явлений при внезапном трехфазном коротком замыкании синхронного генератора
- •3.10. Синхронные двигатели и компенсаторы
- •3.10.1. Синхронные двигатели
- •3.10.2. Синхронный компенсатор
- •Лабораторные работы и контрольные вопросы по разделу «синхронные машины»
- •Исследование характеристик трехфазного синхронного генератора
- •Определение параметров трехфазного синхронного генератора
- •Исследование синхронного реактивного двигателя
- •Параллельная работа синхронного генератора с мощной сетью
- •4. Машины постоянного тока
- •4.1. Устройство простейшей машины постоянного тока и принцип ее действия
- •4.2. Якорные обмотки машин постоянного тока
- •4.2.1. Петлевые обмотки
- •4.2.2. Волновые обмотки
- •4.3. Магнитная цепь машины постоянного тока при холостом ходе
- •4.4. Магнитное поле машины при нагрузке
- •4.5. Коммутация
- •Физическая сущность коммутации
- •Способы улучшения коммутации
- •4.6. Электродвижущая сила обмотки якоря и электромагнитный момент
- •4.6.1. Эдс якоря
- •4.6.2. Электромагнитный момент
- •4.7. Генераторы постоянного тока
- •4.7.1.Общие сведения о генераторах постоянного тока
- •4.7.2. Характеристики генераторов постоянного тока
- •Характеристика холостого хода
- •Внешняя характеристика
- •Регулировочная характеристика
- •Нагрузочная характеристика
- •Характеристика короткого замыкания
- •4.7.3. Параллельная работа генераторов постоянного тока
- •4.8. Двигатели постоянного тока
- •4.8.1. Пуск двигателей постоянного тока
- •4.8.2. Регулирование частоты вращения и устойчивость работы двигателя
- •4.8.3. Рабочие характеристики двигателей постоянного тока
- •4.8.4. Торможение двигателей постоянного тока
- •Лабораторные работы и контрольные вопросы по разделу «машины постоянного тока»
- •Исследования генератора постоянного тока независимого возбуждения
- •2. Исследование генератора постоянного тока параллельного возбуждения
- •Исследование двигателя постоянного тока параллельного возбуждения
- •Исследование двигателя постоянного тока последовательного возбуждения
- •Приложение Вопросы для самопроверки остаточных знаний Раздел "Трансформаторы"
- •Раздел "Асинхронные машины"
- •Раздел "Синхронные машины"
- •Раздел "Машины постоянного тока"
- •Ответы на вопросы по самопроверке остаточных знаний Раздел " Трансформаторы"
- •Раздел "Асинхронные машины"
- •Раздел "Синхронные машины"
- •Раздел "Машины постоянного тока"
- •Список литературы
- •Содержание
- •Электрические машины и трансформаторы Издание шестое, исправленное
1.6. Векторные диаграммы трансформатора при нагрузке
Для их построения используется электрическая схема замещения приведенного трансформатора и основные уравнения напряжений и токов. Векторные диаграммы наглядно показывают соотношения и фазовые сдвиги между токами, ЭДС, напряжениями трансформатора.
Для определения
угла сдвига фаз между векторами
![]() и
и
![]() необходимо знать характер нагрузки.
При активно-индуктивной нагрузке (рис.
1.10) вектор
отстает по фазе от вектора
на угол
необходимо знать характер нагрузки.
При активно-индуктивной нагрузке (рис.
1.10) вектор
отстает по фазе от вектора
на угол
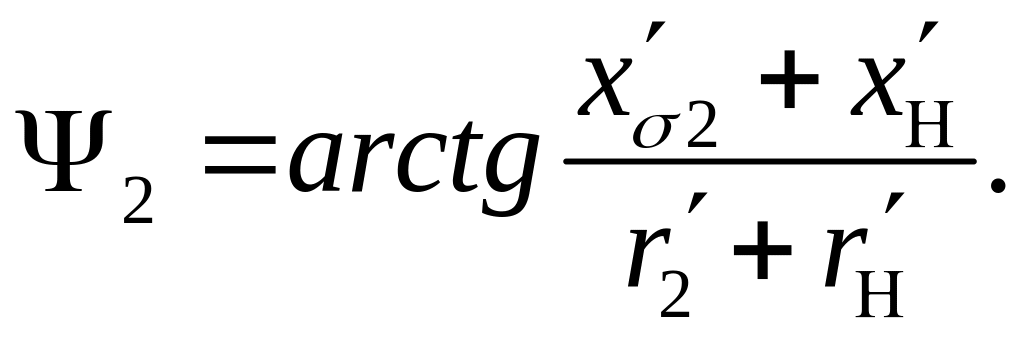
При активно-емкостной нагрузке (рис.1.11) вектор опережает по фазе вектор на угол

Рис. 1.10 |
Рассмотренные
векторные диаграммы нагруженного
трансформатора из-за их сложности не
могут быть использованы для практических
расчетов. По аналогии с опытом короткого
замыкания в трансформаторах, работающих
с нагрузкой близкой к номинальной,
пренебрегают током холостого хода и
считают, что
![]() .
.
Рис. 1.11 |
Упрощенную векторную
диаграмму строят по значениям номинального
напряжения первичной обмотки
![]() номинального тока первичной обмотки
номинального тока первичной обмотки
![]() коэффициента мощности
коэффициента мощности
![]() и параметрам треугольника короткого
замыкания
и параметрам треугольника короткого
замыкания
![]()
Поясним построение
упрощенной векторной диаграммы
трансформатора при активно-индуктивной
нагрузке (рис. 1.12,б). Произвольно, например,
на оси ординат из ее начала строят вектор
тока
![]() Под углом
Под углом
![]() проводят линию, на которой будет
расположен вектор напряжения
проводят линию, на которой будет
расположен вектор напряжения
![]() в соответствии с характером нагрузки.
Строят
в соответствии с характером нагрузки.
Строят
![]() - треугольник короткого замыкания.
Катет ВС, равный активной составляющей
напряжения короткого замыкания, совпадает
по фазе с вектором тока. Катет АВ,
равный реактивной составляющей напряжения
короткого замыкания, опережает по фазе
вектор тока на 90
- треугольник короткого замыкания.
Катет ВС, равный активной составляющей
напряжения короткого замыкания, совпадает
по фазе с вектором тока. Катет АВ,
равный реактивной составляющей напряжения
короткого замыкания, опережает по фазе
вектор тока на 90![]() .
.

Рис. 1.12
Сдвигают
,
не изменяя ориентации его сторон, так,
чтобы вершина С находилась на линии,
направленной под углом
![]() к
вектору тока, до тех пор пока расстояние
от начала координат до вершины А не
станет равным
к
вектору тока, до тех пор пока расстояние
от начала координат до вершины А не
станет равным
![]()
После этого
определяют угол фазового сдвига
![]() между током первичной обмотки
и ее напряжением
между током первичной обмотки
и ее напряжением
![]() а также величину вектора
а также величину вектора
![]() Все построения векторов выполняются в
масштабе.
Все построения векторов выполняются в
масштабе.
1.7. Внешние характеристики трансформатора
Изменение тока нагрузки трансформатора вызывает изменение его вторичного напряжения и коэффициента полезного действия, вследствие изменения падений напряжения и потерь активной мощности в его обмотках.
Изменение вторичного напряжения обычно выражают в процентах и определяют следующим образом:

где
![]() напряжения
(ЭДС) холостого хода вторичной обмотки,
обычное и приведенное, при номинальном
напряжении первичной обмотки;
напряжения
(ЭДС) холостого хода вторичной обмотки,
обычное и приведенное, при номинальном
напряжении первичной обмотки;
![]() напряжения
на клеммах вторичной обмотки трансформатора
при нагрузке, обычное и приведенное,
при номинальном напряжении первичной
обмотки.
напряжения
на клеммах вторичной обмотки трансформатора
при нагрузке, обычное и приведенное,
при номинальном напряжении первичной
обмотки.
Используя упрощенную векторную диаграмму трансформатора, получено выражение для расчета изменения вторичного напряжения
![]()
где
 коэффициент
нагрузки.
коэффициент
нагрузки.
Из данного выражения следует, что изменение вторичного напряжения зависит от величины и характера нагрузки.
Зависимости
![]() при
при
![]() приведенные
на рис. 1.13,а, имеют практически линейный
характер, т.к. первое слагаемое изменяется
пропорционально нагрузке, а второе, в
силу его малости, не оказывает заметного
влияния на значение
приведенные
на рис. 1.13,а, имеют практически линейный
характер, т.к. первое слагаемое изменяется
пропорционально нагрузке, а второе, в
силу его малости, не оказывает заметного
влияния на значение
![]() .
.

Рис. 1.13
Вторым слагаемым пренебрегают в большинстве случаев из-за его относительно малого значения и используют для расчета упрощенную формулу
![]()
Зависимость
![]() при
при
![]() имеет более сложный вид, рис. 1.13,б. При
имеет более сложный вид, рис. 1.13,б. При
![]()
![]() ,
при
,
при
![]()
![]() .
Наибольшее изменение напряжения имеет
место при
.
Наибольшее изменение напряжения имеет
место при
![]() и равно
и равно
![]() .
При
.
При
![]() изменения напряжения нет,
изменения напряжения нет,
![]()
Внешней характеристикой трансформатора называют зависимость
Рис. 1.14 |
Для построения внешней характеристики может быть использована формула
![]() где
где
![]() .
.
Внешние характеристики
(рис.1.14) вследствие линейности зависимости
![]() также линейны.
также линейны.



