Методика оптимізації функції методом найшвидшого спуску
Нагадаємо деякі поняття. Якщо функція f(X) диференційована в точці Xo, то градієнтом f(X) у точці Xo=(x10,x20,...,xno) називається n - вимірний вектор:
f(x0) = ( f(x0)/ x1,…, f(x0)/ xn) = (1 f(x0),2 f(x0),…, n f(x0)).
Вектор-градієнт спрямований по нормалі до лінії рівня поверхні f(X) = C (рисунок 6) і показує напрямок найшвидшого зростання функції в даній точці. Вектор f(Xo), протилежний градієнту, називається антиградієнтом і спрямований убік найбільшого зменшення функції f(X). У точці мінімуму градієнт функції дорівнює нулю. Тоді, вибравши за напрямок спуска Рк у виразі (7) антиградієнт функції f(X) у точці Xk, одержимо такий ітераційний процес
Xk+1=Xk - k f(Xk), k>0, k=0,1,... (8)
У координатній формі цей процес можна записати:
xik+1=xik
- ki
f(Xk),
i=
.
Всі ітераційні процеси, в яких напрямок руху на кожнім кроці збігається з антиградієнтом (градієнтом) функції, називають градієнтними. Вони відрізняються між собою тільки способами вибору величини кроку к.
Найбільш економними за кількістю ітерацій і надійними, є градієнтні методи зі змінним кроком, зокрема метод найскорішого спуску. Тут величина кроку k на кожній ітерації вибирається за умови мінімуму функції f(X) у напрямку спуска, тобто
f(Xk
- k
f(Xk))
=
f(Xk
-
f(Xk)).
(9)
Отже, в цьому варіанті градієнтного методу на кожній ітерації необхідно вирішувати задачу одновимірної мінімізації цільової функції уздовж градієнтного напрямку.
Необхідну ознаку екстремуму функції f(X) у напрямку спуска можна записати у вигляді скалярного добутку векторів
( f(Xk+1), f(Xk)) = 0. (10)
Алгоритм методу найскорішого спуску полягає в наступному:
Етап 1. Обчислити у початковій точці X0 значення градієнта f(X0).
Етап 2. Знайти величину кроку 0 шляхом розв’язання задачі одновимірної мінімізації (9).
Етап 3. Перейти у напрямку антиградієнту – f(X0) з визначеним на етапі 2 кроком 0 в нову точку X1 у відповідності з формулою: X1=X0 – k f(X0).
Етап 4. Продовжити пошук: на k-му кроці в точці Xk обчислити значення градієнта f(Xk) і величину кроку k та здійснити спуск у точку
Xk+1=Xk- k f(Xk).
Етап 5. Пошук оптимуму припинити при виконанні однієї з наступних умов:
1) при виконанні критерію кінця ітераційного процесу k < min;
2) при значеннях норми вектор-градієнта менше заданого значення
||f(x)||=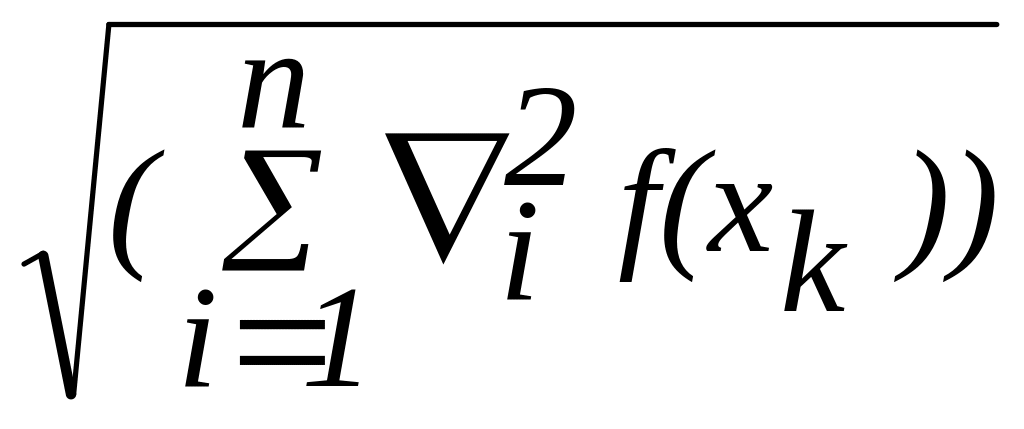
<min.
Приклад мінімізації функції методом найшвидшого спуску
Мінімізувати функцію двох змінних
f(x1,x2)
= -6x1
- 4x2
+ x
+
x
+
18.
(11)
1 Виберемо довільну точку X0=(1,5;3). У цій точці f(X0)=8,25. Обчислимо вектор-градієнт функції в точці X0:
Тоді
f(X0) = (-3;2).
Оскільки f(X0) 0, то X0 не є точкою екстремуму.
2 Переходимо з Х0 в напрямі антиградієнту - f(X0) в нову точку Х1 у відповідності з формулою:
X1 = X0 - 0 f(X0).
тобто X1 = (1,5 + 30; 3 - 20).
Для визначення координат точки Х1 потрібно визначити значення кроку 0. Одержимо:
f(X1) = (-3 + 60; 2 - 40).
У відповідності з (10) ( f(Xk+1), f(Xk)) = 0 маємо:
(-3+60)(-3)+(2-40) 2=9 - 180 + 4 - 80 =13 -260=0.
Звідки 0 = 0,5.
3 При 0 = 0,5 зменшення функції в напрямку антиградієнта досягає найбільшої величини. Здійснимо спуск з обраним кроком у точку X1:
X1 = (3; 2).
Обчислимо значення функції в точці Х1 (підставимо координати точки Х1 у вираз (11) і одержимо:
f(X1) = 5 < f(X0).
4 Визначимо вектор-градієнт в точці Х1:
1f(X1) = -6 + 2 3 = 0;
2f(X1) = -4 + 2 2 = 0,
тобто f (3,2) = (0;0).
Це означає що, ніякими переміщеннями з точки Х1 функцію f(X) зменшити не можна і Х1 - шукана точка мінімуму Х*. Отже,
X*
= (x
, x
) = (3;2); fmin=5.
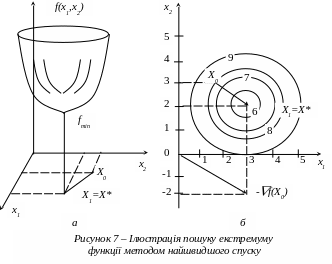
На рисунку 7 наведена геометрична інтерпретація розв’язання задачі. На рисунку 7а приведене наглядне зображення поверхні f(X) - параболоїд обертання, на рисунку 7б поверхня f(X) зображена лініями рівня - концентричними колами. Антиградієнт -f(X0)=(3;-2) побудовано в початку координат. Траєкторія найшвидшого спуску Х0Х1 у точку мінімуму Х* паралельна антиградієнту -f(X0).
Відомо, що квадратичну функцію вигляду (11) можна представити еквівалентно і так:
(x1 - x )2 + (x2 - x )2 = (f - fmin)/a, (12)
де а - коефіцієнт при x і x у виразі (11).
Вираз (12) задає у загальному вигляді рівняння сімейства кіл (ліній рівня) радіуса
R
=
.
Отже, для побудови ліній рівня поверхні f(X) її рівняння (11) приведемо до такого виду (для а=1):
(x1 - 3)2 + (x2 - 2)2 = f - 5. (13)
Лініями рівня поверхні (13) при f=c будуть кола. При f=6;7;8;9 їх радіуси відповідно дорівнюють 1; 1,41; 1,73; 2. В проекції на площину x1 О x2 вони мають загальний центр з координатами (3;2).
У розглянутому прикладі мінімум квадратичної функції був досягнутий методом найшвидшого спуску за один крок. При мінімізації більш складних функцій кількість ітерацій буде значно більшою.