27. Понятие формальной модели обработки информации. Понятие абстрактной машины. Машина Тьюринга.

Машина Тьюринга состоит из:

1) управляющего устройства, которое может находиться в одном из состояний, образующих конечное множество ;

2) ленты, разбитой на ячейки, в каждой из которых может быть записан один из символов конечного алфавита;

3) устройства обращения к ленте, т. е. считывающей и пишущей головки, которая в каждый момент времени обозревает ячейку ленты, в зависимости от символа в этой ячейке и состояния управляющего устройства записывает в ячейку символ (быть может, совпадающий с прежним или пустой, т. е. стирает символ), сдвигается на ячейку влево или вправо или остается на месте; при этом управляющее устройство перехо­дит в новое состояние (или остается в старом). Среди со­стояний управляющего устройства выделены начальное состояниеи заключительное состояние, которое будемобозначать (z здесь понимается не как числовая пере­менная, а как мнемонический знак конца). В начальном состоянии машина находится перед началом работы; по­пав в заключительное состояние, машина останавливается. Таким образом, память машины Тьюринга — это конеч­ное множество состояний (внутренняя память) и лента (внешняя память). Лента бесконечна в обе стороны, од­нако в начальный момент времени только конечное число ячеек ленты заполнено непустыми символами, остальные ячейки пусты, т. е. содержат пустой символ (пробел), Из характера работы машины следует, что и в любой по­следующий момент времени лишь конечный отрезок лен­ты будет заполнен символами. Поэтому важна не факти­ческая (как говорят в математике, актуальная) бесконеч­ность ленты, а ее неограниченность, т. е. возможность писать на ней сколь угодно длинные, но конечные слова. Данные машины Тьюринга — это слова в алфавите ленты; на ленте записываются и исходные данные, и окончатель­ные результаты. Элементарные шаги машины — это считы­вание и запись символов, сдвиг головки на ячейку влево и вправо, а также переход управляющего устройства в сле­дующее состояние. Детерминированность машины, т. е. по­следовательность ее шагов, определяется следующим об­разом: для любого внутреннего состоянияи символаоднозначно заданы: а) следующее состояние; б) символ , который нужно записать вместов ту же ячейку (стирание символа будем понимать как запись пустого символа ); в) направление сдвига головки, обозначаемое од­ним из трех символов: L (влево), R (вправо), Е (на месте). Это задание может описываться либо системой правил (команд), имеющих вид

либо таблицей, строкам которой соответствуют состояния, столбцам — входные символы, а на пересечении строкии столбца записана тройка символов, и, наконец,блок-схемой, которую будем называть диаграммой периодов.

Недетерминированная машина Тьюринга моделирует алгоритмы с некоторой «свободой выбора», причем нас интересует, сколько времени понадобится, если с выбором «всегда будет везти». По крайней мере некоторые команды недетерминированной машины Тьюринга NT при одной и той же истории ее работы и, значит, при одном и том же ее полном состоянии могут выполняться разными способами. Для каждого внутреннего состояния машины и читае­мого с ленты символа эти способы заданы.

У машины Тьюринга NT также имеется конечный набор внутренних состояний , и алфавит символов на ленте _, тоже конечен. Однако правила

действии имеют вид списков:

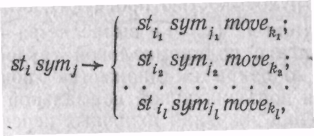
гдеl — это максимальное число вариантов выполнения действия. Если для некоторых внутренних состояний и чи­таемых символов sym_j вариантов меньше, то последний будем дублировать так, чтобы их стало l.

Перед выполнением очередного действия из одной машины возникает l машин. Записи на их лентах одинаковы — такие, какие были у их «предка», но с этого момента их пути расходятся: каждая машина выполняет свой ва­риант действия из списка. Процесс работы детерминированной машины Тьюринга Т (и любой рассмотренной раньше машины) может быть изображен в виде линейной после­довательности действий, а процесс работы недетерминиро­ванной машины NT — в виде дерева, вершинами которого являются выполняемые действия, а ребрами — переходы от одного действия к следую­щим (рис. 9.2). Таким обра­зом, она одновременно ре­шает задачу разными спо­собами, чтобы не упустить тот, при котором «везет». Каждый способ — это по­следовательность машин­ных операций, которой соот­ветствует цепь дерева рабо­ты машины NT с началом в корне.

Если по некоторой цепи действия заканчиваются, то возможны два исхода: задача решена или решение не найдено. В первом случае все ос­тальные машины, размножившиеся к этому моменту, тоже кончают работу и превращаются в одну машину. Во вто­ром — они продолжают работать. Если же по всем цепям произойдет окончание вычислений с отрицательными ре­зультатами, то все машины тоже сливаются в одну: задача не имеет решения. Других обменов информацией между различными вариантами процесса работы машины не про­исходит.