20. Локальные степени графа.Части графа и подграфы.

Всё,что свойственно для множеств характерно и для графов.

Недментиров. Граф – локальная степень графа в вершине а назыв число рёбер инцидентных вершине а (ρ(a)). Локальная степень связана с кратностью ребра

Каждое ребро в графе участвует дважды при подсчёте локальных степеней. v-количество ребёр.

Сумма всех локальных степеней всех вершин в графе – четное число.Если из этой суммы вычесть четные слагаемые,то оставшаяся сумма – четное число, она содержит только нечетные слагаемые. Чтобы сумма слагаемых была четным числом,надо чтобы число слагаемых было четным.Число вершин нечётной локальной степени – четное.

Для ориентир. Графов вводят полустепень исхода и захода.

Полустепень исхода вершины а – число ребер исходящих из а,полустепень захода – число входящих в а.

Однородный неориентированный граф – если локальные степени во всех вершинах равны.

Разложим геометрические фигуры,представленные однородными графами.

V=2 v=3

2ve=nv

Ve=(nv)/2

V=3 n=8 ve=12

Части графа и подграфы.

G1=(E1,x)

G2=(E2,x)

G2 называют частью G1 если множество ребер Е2 является подмножеством множества Е1 (Е2 С Е1).

Подграф G(A) графа G(Е,х) такая часть графа G ,которая содержит ребра,вершины которых лежат в множестве А.

Нуль – граф- граф,в котором есть множество вершин но нет ниодного ребра.

Полный граф- в котором есть все возможные ребра.

Граф конечный или бесконечный – по числу ребер,входящих в граф.

21. Эйлеровы графы.

Задача- составить маршрут прогулки, начинающейся в какой- либо части города, проходящей по всем мостам по одному разу и возвращающийся в ту же часть города.

Дан граф, найти цикл проходящий

По всем рёбрам по одному разу.

Цикл наз-ся Эйлеровым, граф – Эйлеровым.

Эйлерова цепь - цепь проходящая по всем рёбрам в точн. по одному разу.

Теорема Эйлера:

Граф Эйлера – граф, когда он связен и локальная степень всех вершин четная.

Док-во:

1). Необходимость

А) пусть в графе существует Эйлеров цикл, он связен.

Б) Цикл в каждую ветвь заходит по разному ребру входит и по- другому выходит. Значит локальные степени четные.

2). Достаточность

Предположим, что в кратных связях , что в нем можно построить Эйлерову цепь. Приступим к построению Эйлеровой цепи. Построение может начинаться с любой вершины.

А Л Г О Р И Т М(нач с любой вершины)

Процесс построения цикла заключается в подключении к нему всё новых ребер так чтобы ниодно не повторилось.

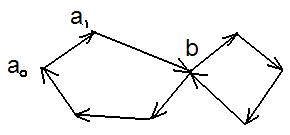
Этот процесс может закончиться в вершине Построенный циклначинающийся ви зака-

нчивающийся в . Каждое ребро только один раз. Этот цикл может включать в себя рёбра или не включать если первое- то проходит.должен иметь хотя бы одну вершину. Найдётся вершина Р, которая инцидентна как циклу Р так и графу. Пусть из вершиныb на графе строится циклпроходящий по новым рёбрам графа(по остальным ). Он может закончиться только в. из 2-х циклов Р1 и Р2 имеем новый цикл

Цикл Р1 в b разорвём , вставим туда Р2:

Новый цикл может включать все рёбра и не включать.

Если включает , то найдётся такая вершина С , которая инциндентна как Р1 , так и всем остальным рёбрам.

СЛЕДСТВИЕ 1

В графе существует Эйлерова цепь тогда и только тогда , когда он связен и имеет в точности 2 вершины локальной степени нечетной.

Пусть имеется граф и в точности 2 вершины имеют нечетные локальные степени.

Введём активное ребро АВ(дополним граф) тогда граф будет Эйлеровым. Будет расширенным. Построим в нём Эйлеров цикл, а затем удалим из этого цикла фиктивное ребро АВ. Тогда цикл расходится в цепь с конечными вершинами А и В.

Существует граф связный . ½ к не пересекается ребром цепей , где к- число вершин нечетной локальной степени.

Граф будет Эйлеров.Граф может быть представленввиде суммы графов неперскающихся цепей(граф распадается).

Для ориентированных графов: контур существует , когда связен и в каждой вершине полустепень исхода= полустепени захода.