24. Деревья. Основные понятия и определения.
Связный граф без циклов - дерево. Граф без циклов-лес.
В этом графе нет петель и без кратных рёбер.
В графе изображение вершин и рёбер произвольное, а в деревьях сущ. правила
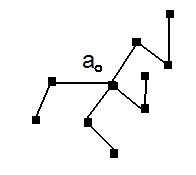
-корень,
все инцинд. ей верш. изобр. на одном
уровне ниже . Рёбра провод
Линиями прерывн. Проводятся все соседние вершины. Вершины одного уровня- ранги. Все соседн. верш. с Верш. 1-го ранга и т.д.
Деревья, в которых выбран корень называются корневыми.
Вершины, которым инцидентно только одно ребро называются листьями или висячими вершинами.
b-
родительская для e
и f
(e
и f
-сыновье)
Бинарные деревья – деревья, каждая вершина которых, кроме висячих, имеет две дочерние.
Ориентированные и неориентированные деревья.
Ориентированно дерево – корень – это вершина, имеющая только исходящие ребра.
Теорема.
Дерево на n вершинах имеет в точности (n-1) ребро.
Доказательство.
При n=2.
Предположим, что в дереве на n вершинах (n-1) ребро.
Добавим еще одну вершину.
Для тог, чтобы граф
был связн, надо соединить новую вершину
со старым ребром
при добавлении одной вершины добавляется
одно ребро.
25. Задача о минимальном соединении (построение дерева-остова).
Задача о минимальном соединении – одна из оптимизационных задач. Она рассматривается только для связных графов.
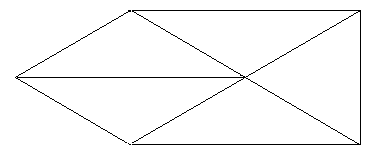
Дерево-остов Т графа G – такая часть графа G, которая имеет то же самое множество вершин и не имеет циклов:
G T1 T2
Постановка задачи:
Дано n городов, расстояние между ними. Построить сеть дорог, связывающих эти города и имеющие минимальную длину.
Теорема Кэли:
Число деревьев, которые можно построить на n вершинах:
Алгоритм:
- часть дерева
,
которая содержит
ребер.
- Построение дерева
начинается с построения
:
1). Выбор первого ребра (минимальной длины).
2). Пусть часть
дерева
уже построена. Если
не включает все вершины, то надо построить
и т.д. Это ребро ((i+1)-е
ребро) должно иметь общую концевую
точку с частью
и не образовывать цикла. Если таких
ребер несколько, то выбирают ребро
минимальной длины.
26. Деревья. Задача о минимальном пути.
Задача о минимальном (кратчайшем) пути – одна из оптимизационных задач.
Постановка задачи:
Дан связный граф с нагруженными ребрами. Найти кратчайший путь, связывающий две данные вершины.
x2
(1) x6
= xn
(6)
5
1 5
(0) 7 x4 (3) 2
x1
10 2
1
x3 (10) x5 (5)
Алгоритм:
Разметка вершин:
а). Метку в вершине
обозначим
(в
вершине
метка
=0).
Пусть имеется
множество размеченных и множество
неразмеченных вершин и пусть
- одна из неразмеченных вершин, соседних
с размеченными.
б). Этой вершине приписывается метка:
,
Где
- соседняя вершине
и размеченная.
Возможны два случая:
- в результате
конечная вершина
стала размеченной, тогда процесс разметки
закончился.
-
- неразмеченная вершина, тогда множество
размеченных вершин увеличилось,
возвращаемся к пункту б) для новой
вершины
до тех пор, пока
не окажется размеченной.
Метка в последней
вершине равна длине кратчайшего пути
от
к
.
Осталось найти сам путь.
Построение кратчайшего пути начинается с вершины
.
Надо найти предпоследнюю вершину. В качестве предпоследней вершины выбирается такая, чтобы:
В качестве вершины
выбирается такая, чтобы:
Где
- метка вершины
,
последней найденной в пути.
Метка может представлять пару
,
где
- последняя вершина, которая была
использована в алгоритме, такая, что:
