Прямое произведение графов

Пусть и – два одновременно ориентированных или неориентированных графа с непересекающимися множествами вершин.Прямым произведением графов называется граф со множеством вершин , в котором дуга (ребро) из вершины в вершину существует тогда и только тогда, когда существуют дуги (рёбра) и одновременно.

Рассмотрим выполнение операции прямого произведения графов в матричной форме.

Теорема 2.2.6.Пусть и – два одновременно ориентированных или неориентированных графа с непересекающимися множествами вершин, – матрицы смежности их вершин соответственно. Тогда матрицей смежности вершин графа является матрица размерности , в которой элемент , указывающий количество дуг (рёбер), соединяющих вершину с , вычисляется следующим образом:

,

где и – элементы матриц соответственно, , .

Размерность матрицыAравна , а . По определению, в графе существует дуга (ребро), идущая из вершины в вершину , тогда и только тогда, когда одновременно существуют дуги (рёбра) и . Элемент матрицы смежности А графаG определяет количество дуг (рёбер) из вершины в вершину . Нахождение количества дуг (рёбер) графов и , для которых одновременно и , соответствует операции взятия минимума элементов и матриц соответственно.

Следствие.Если графы и не имеют кратных дуг (рёбер) и петля в неориентированном графе не считается двойной, то при вычислении элементов матрицы смежности вершин графа операция взятия минимального элемента соответствует вычислению обычного или логического произведения:

.

Замечание.Для упрощения и ускорения процесса вычисления элементов матрицы смежности вершинAграфа воспользуемся следующим наблюдением. Не ограничивая общности, будем считать, что . Упорядочим столбцы и строки матрицыAследующим образом: Тогда матрицуAможно разбить на блоков, соответствующих элементам матрицы А₁, размерностью . Элемент каждого блока имеет фиксированныеiиkи будет вычисляться как , причём – фиксированный элемент матрицы А₁. Если элементы матриц А₁и А₂принимают только значения 0 и 1, то – прямое (тензорное) произведение матриц:

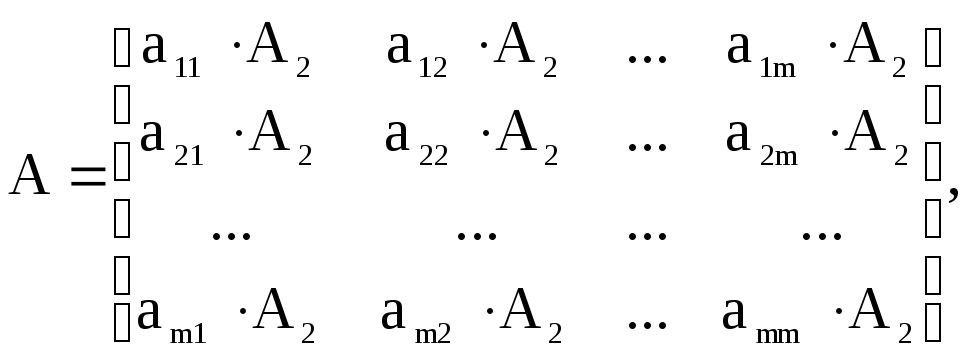
где скалярно умножается на матрицу А₂. равно 0, если , и равно А₂, если .

Пример 2.2.6.Выполнение операции прямого произведения графов изображено на рис. 2.2.12.

Очевидно, что соответствие между элементами множеств и определяет изоморфизм графов и , что справедливо и в общем случае.

Рис. 2.2.12

Составим матрицы смежности вершин исходных графов и .

, .

Согласно следствию из теоремы 2.2.6 и замечанию, матрица смежности вершин графа имеет вид:

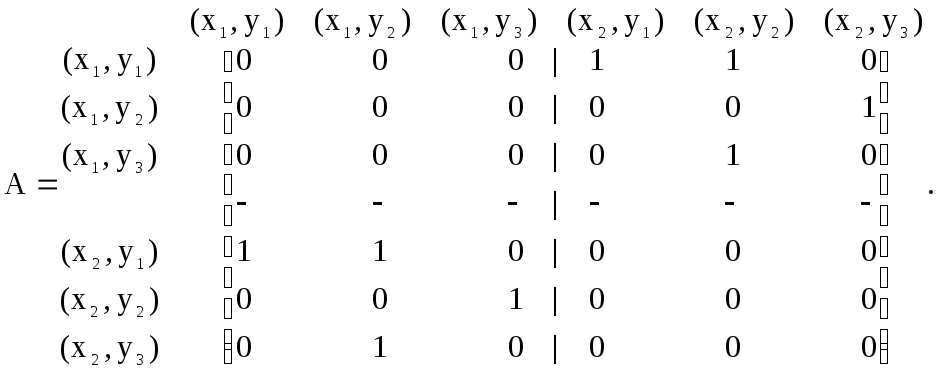
Нетрудно убедиться в том, что матрица смежности вершин А соответствует графу , изображённому на рис. 2.2.12.

Операция прямого произведения графов обладает следующими свойствами, которые следуют из определения, а также свойств декартова произведения множеств и справедливы для любых одновременно ориентированных или неориентированных графов с непересекающимися множествами вершин:

1. – свойство коммутативности;

2. –свойство ассоциативности.

Операцию прямого произведения можно распространить по индукции на любое конечное множество ориентированных или неориентированных графов с попарно не пересекающимися множествами вершин:

.