5. Розробка моделі виміру координат цілі по даним двопозиційної рлс

Н а рис. 5.1 наведене розташування ДП РЛС і цілі в декартовій системі координат пов'язаної із прийомною підсистемою. Показано координати передавальної системи й вимірювані параметри цілі в сферичній системі координат.

Рис.5.1

Як відзначалося вище, азимут і кут місця цілі виміряються прийомною підсистемою ДП РЛС прямим способом. При цьому рівняння виміру для й на k- му кроці мають вигляд:

(5.1)

(5.2)

де , – обмірювані значення азимута й кута місця цілі відповідно; , – справжні значення азимута й кута місця цілі відповідно; , – помилки виміру азимута й кута місця, що є білими гаусовськими шумами з нульовими середніми й дисперсіями , відповідно.

Рівняння виміру різниці відстаней Δ, які проходять перевідбитий від цілі сигнал і прямій сигнал від передавальної підсистеми на k-му кроці має вигляд:

(5.3)

де – вимірюване значення різниці відстаней, які проходять перевідбитий сигнал від цілі та прямий сигнал від передавальної підсистеми; – справжнє значення різниці відстаней, що визначається по формулі

- справжня відстань між прийомною підсистемою й ціллю, – справжня відстань між передавальною підсистемою й ціллю; – база ДП РЛС, що покладається відомої точно й не змінюється в часі; – помилка виміру різниці відстаней, яка є білим гаусовським шумом з нульовим середнім і дисперсією .

Дальність до цілі в ДП РЛС виміряється непрямим способом. Рівняння виміру дальності до цілі на k-му кроці має вигляд [8]:

,

(5.4)

де _, - координати передавальної підсистеми, які покладаються відомими точно й не змінюються в часі.

Зв'язок між вимірами ДП РЛС, виконаними в сферичній системі координат і координатами цілі в декартовій системі координат описуються рівняннями:

(5.5)

(5.6)

(5.7)

Визначимо помилки виміру ДП РЛС у декартовій системі координат. Рівняння виміру дальності до цілі (5.4) є нелінійним. Розкладаючи нелінійні функції у вираженні (5.4) у ряд Тейлора щодо справжніх значень і обмежуючись розглядом лінійних членів можна записати лінеарізоване рівняння виміру дальності до цілі у вигляді:

(5.8)

де – справжнє значення дальності до цілі; – помилка виміру дальності до цілі, що визначається по формулі

коефіцієнти визначаються на основі виразів:

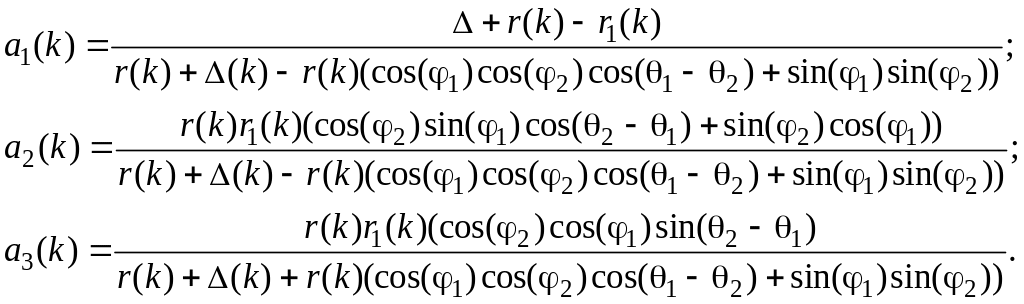
Рівняння (5.5)-(5.7), що описують зв'язок між вимірами ДП РЛС, виконаними в сферичній системі координат і координатами цілі в декартовій системі координат також є нелінійними. Підставимо вирази (5.1), (5.2), (5.8) у рівняння (5.4)-(5.6). Розкладаючи нелінійні функції в рівняннях (5.5)-(5.7) у ряд Тейлора щодо справжніх значень і обмежуючись розглядом лінійних членів можна записати лінеарізовні рівняння виміру РЛС у декартовой системі координат у вигляді:

(5.9)

(5.10)

(5.11)

де – помилки вимірів по відповідних осях декартовій системи координат, які визначаються по формулах

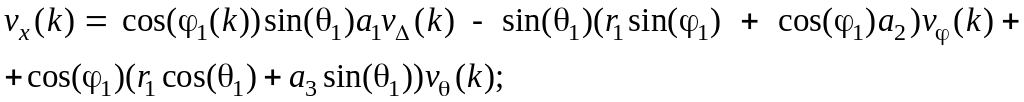
(5.12)

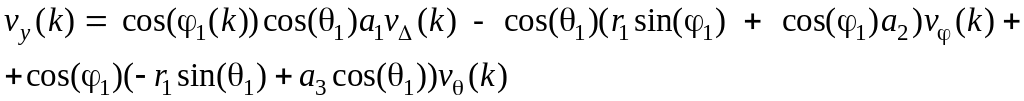
(5.13)

(5.14)

З виразів (5.12) - (5.14) треба, що помилки виміру в декартовій системі координат є функціями сферичних координат цілі й не є стаціонарними.

Оскільки помилки виміру ДП РЛС мають нульові математичні очікування з виразів (5.12) - (5.14) треба , щоб середні значення помилок вимірів також дорівнюють нулю. За методикою обчислення других моментів випадкових величин /2/, можна також показати, що дисперсії й взаємні кореляції помилок вимірів в декартовій системі координат описуються виразами:

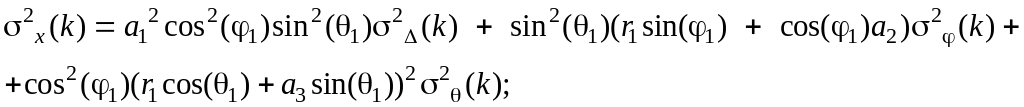
(5.15)

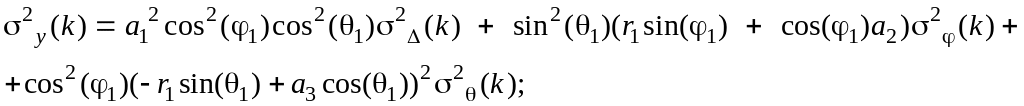
(5.16)

(5.17)

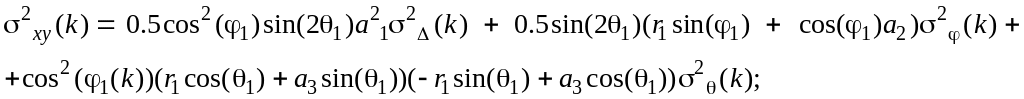(5.18)

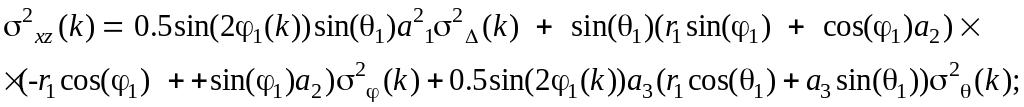(5.19)

(5.20)

Аналіз отриманих точносних характеристик ДП РЛС виконаний для випадку вимірення координат цілі на площині ХОY, при цьому кути місця , і дисперсія помилки виміру кута місця покладалися рівними нулю, а =80м, На рис 5.2,а в полярній системі координат (R, ) показане умовне розташування приймача (0 м, ), передавача (25000 м, ) і цілі, що переміщається по окружності R=50000 м. На рис 5.2,б і 5.2,у показані залежності СКВ помилок визначення координат цілі по осях декартової системи координат X, Y, а на мал. 5.2,г залежність модуля коефіцієнта взаємної кореляції цих помилок від кута приходу перевідбитого сигналу. На мал. 5.2,г суцільна лінія відповідає позитивним значенням коефіцієнта взаємної кореляції , а штрихова – негативним значенням.

Рис. 5.2,а Рис. 5.2,б

Рис. 5.2,в Рис. 5.2,г

Як треба з отриманих результатів, СКВ помилок визначення координат цілі по осях декартової системи координат X, Y і коефіцієнт взаємної кореляції залежать від кута приходу перевідбитого сигналу. Основний внесок у помилки визначення координат цілі в декартовій системи координат вносить помилки виміру азимута . Відповідно СКВ помилки досягає максимального значення в області кутів , а СКВ помилки - в області кутів . Із збільшенням дальності до цілі СКВ помилок визначення координат цілі збільшуються. При цьому характер їхньої зміни при розглянутому положенні приймальні й передавальній підсистемам залишається сталим.

Як треба з мал. 5.2,г, існує значна кореляція між помилками виміру в декартовій системі координат. Мінімальні значення кореляції помилок досягається в області кутів . Це обумовлено тим, що основний внесок у помилки виміру по осях декартової системи координат вносять різні помилки , , які є незалежними.

На мал. 5.3,а показаний другий випадок прийому сигналу, коли ціль перебуває між передавачем і приймачем

Рис. 5.3,а Рис. 5.3,б

Рис. 5.3,в Рис. 5.3,г

Як і в попередньому випадку на мал. 5.3,б, 5.3,в і 5.3,г показані залежності СКВ помилок визначення координат цілі по осях декартової системи координат X, Y і коефіцієнта взаємної кореляції від кута приходу перевідбитого сигналу. Невизначеність координат при куті пояснюється одночасним приходом прямого й перевідбитого сигналу, від передавача й цілі відповідно, внаслідок чого в рівнянні виміру дальності (5.4) з'являється невизначеність обчислення.

Як видно з наведеного аналізу помилки визначення координат цілі в декартовій системі координат є функціями її сферичних координат і є нестаціонарними. Зі збільшенням дальності до цілі СКВ помилок визначення координат цілі збільшуються, при цьому основний внесок вносять помилки виміру кутових координат. Існує значна кореляція між помилками виміру в декартовій системі координат, що необхідно враховувати при розробці алгоритмів вторинної обробки радіолокаційної інформації.

Отримані в розділах 4 і 5 модулі руху цілі (4.8) і лінеарізовані рівняння ДП РЛС (5.9)-(5.14) дозволяють застосувати для рішення завдань траєкторної фільтрації апарат калманівської фільтрації.