ЛЕКЦИЯ 04

Тема лекции: Политропные процессы. Реальные рабочие тела, пары

План лекции: 1. Понятие политропного процесса и основные соотношения.

2. Частные случаи политропных процессов.

3. Твердое, жидкое и газообразное (парообразное) состояние вещества». p-v диаграмма изменения состояния.

4. Тепловые характеристики паров.

1. Понятие политропного процесса и основные соотношения

Введём в рассмотрение коэффициент энергетической направленности термодинамического процесса, определяемый выражением:

(4-1)

который показывает, как часть подведённого тепла идет на изменение внутренней энергии

Запишем 1-ый закон термодинамики:

, отсюда

где - величина  показывает какая часть подводимого тепла идёт на совершение работы.

Процессы, в которых в течении всего времени = const носят название политропных процессов.

Величины  и  очень удобны для установления эффективности тех или иных термодинамических процессов (чем больше  и меньше , тем эффективнее процесс).

Однако использование этих величин для описания и анализа процесса затруднительно, поэтому получим уравнение политропного процесса через его показатель n и свяжем с ним величины  и .

Запишем уравнение 1-го закона термодинамики в форме:

и

Произведём замену: ; ;

, тогда можно записать

(а) и

(б) , деля (а) на (б) получим

(4-2)

Для политропного процесса с , с_р и с_V - постоянные величины, тогда для этого процесса n=const

Из выражения (4-2) получим

(4-3)

(4-3) – дифференциальное уравнение политропы.

Интегрируя (4-3) найдём

, или

(4-4)

(4-4) – интегральное уравнение политропы.

Найдём взаимосвязь между  и n.

Из (4-1) получим, что

, откуда (4-5)

Подставив (4-5) в (4-2) получим:

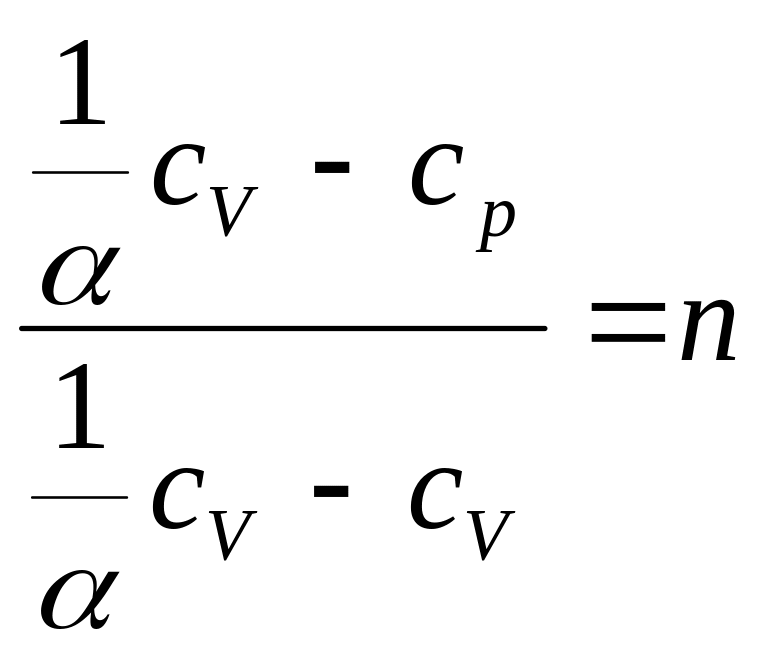, числитель и знаменатель разделим на c_v , получим:

, приводим к общему знаменателю, получим

(4-6)

Разрешая (4-6) относительно  найдём что

(4-7)

Подставляя (4-7) в (4-5), получим, что (4-8)

- теплоёмкость политропного процесса.

Найдём соотношение между параметрами в политропном процессе.

Уравнение политропы (4-4) запишем в виде:

, найдём

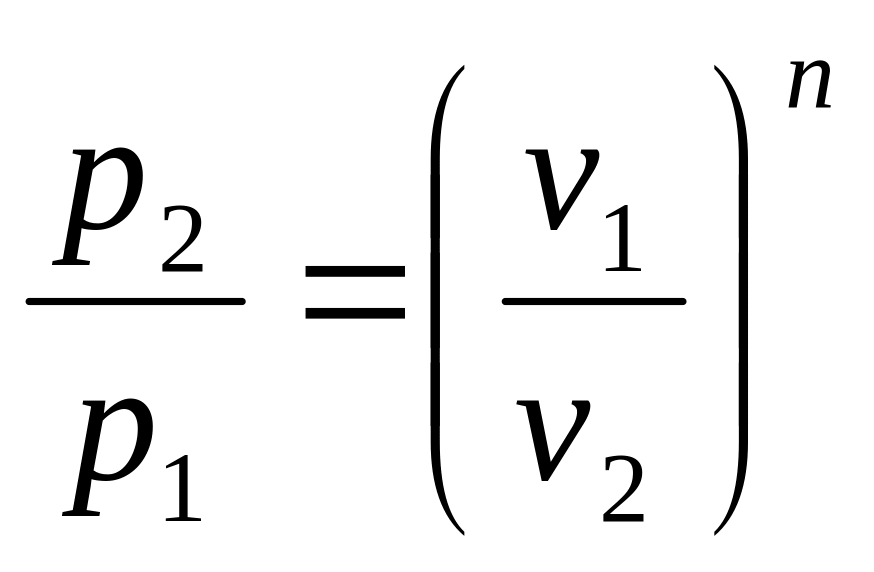(в)

Используя уравнение состояния можно найти, что

(г)

Подставляя (г) в (в), найдём:

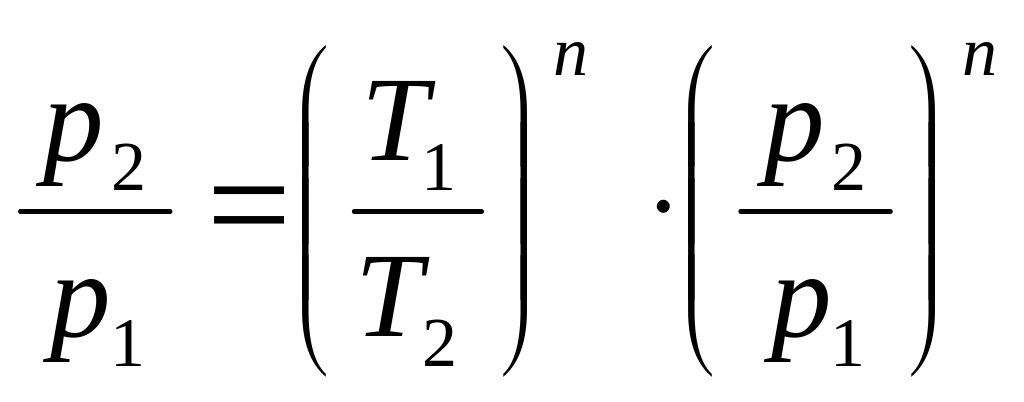, или 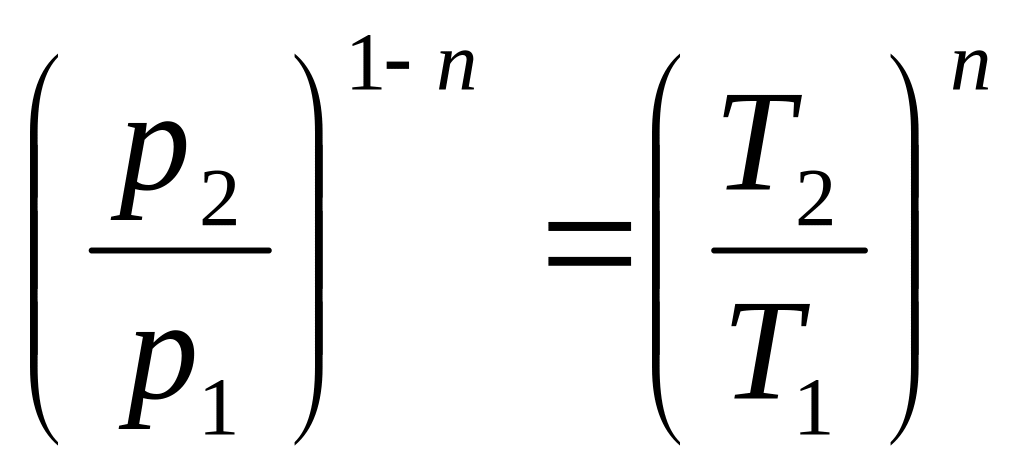откуда

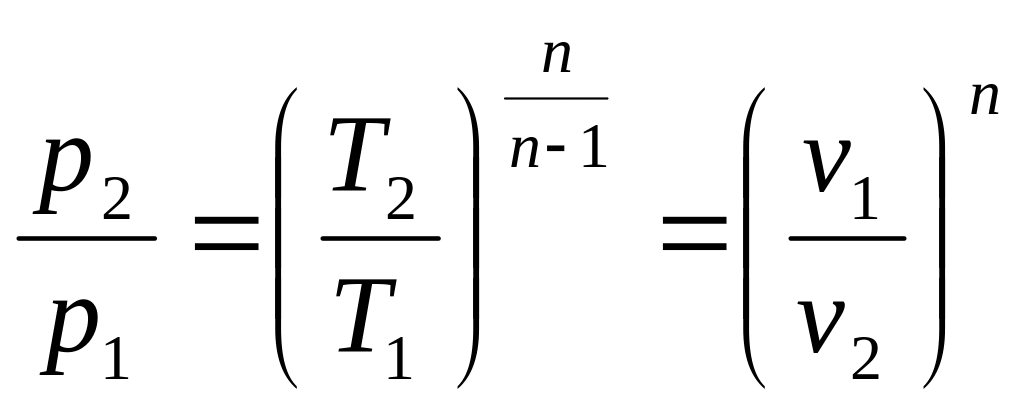, или используя (в), получим

(4-9)

В другом виде соотношение между параметрами в политропном процессе будет:

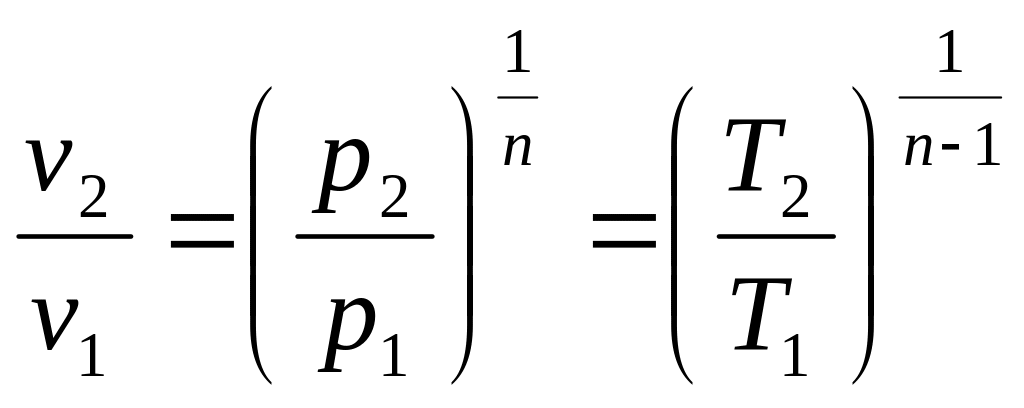(4-10),

или относительно , получим:

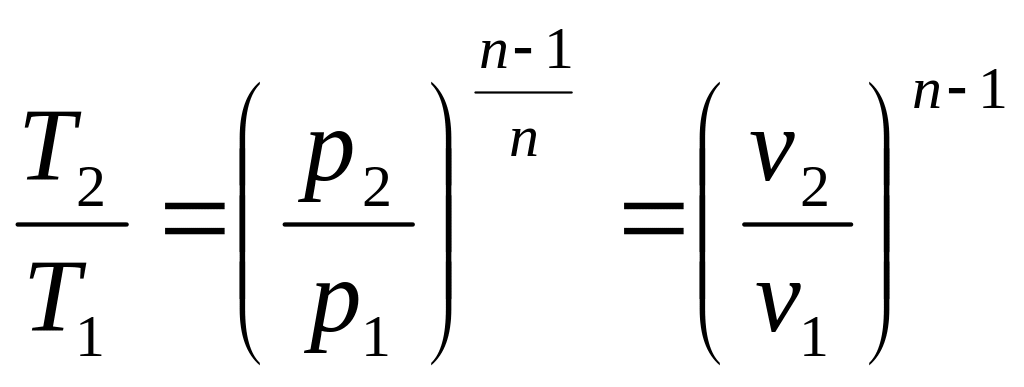(4-11)

Работа политропного процесса может быть найдена из общего определения работы

, из уравнения (4-4) политропы

, откуда

Интегрируя последнее выражение, найдем, что

(д)

Внесём в скобки в уравнении (д) выражение для А, получим, что

(4-12)

(4,12) - выражение для работы политропного процесса

(4-13)

или, выражая подведённое тепло:

(4-14)

При известном показателе политропы n и при известном изменении температуры в процессе, тепло политропного процесса определяется выражением

(4-15)