
- •2.Жидкости,основные физ-кие св-ва. Неньютоновские жидкости.
- •3.Силы, действующие в жидкости.
- •4.Гидростатические давление, его свойства.
- •5.Дифференциальные уравнения равновесия жидкостей.
- •6.Основные уравнения гидростатики(оуг), его геометрическая и энергетическая интерпретация.
- •7.Силы гидростатического давления действующие на плоские поверхности конечного размера.
- •8.Определение центра избыточного давления.
- •9. Силы гидростатического давления действующие на криволинейные поверхности.
- •10.Плавание тел - общие сведения. Определение подъемной силы, действующей на тело, погруженное в жидкость.
- •11.Основные задачи гидродинамики. Виды движ-я жид-ти. Струйная модель потока.
- •12.Гидравлические уравнения неразрывности для элементарной струйки и потока жидкости.
- •13.Дифференциальные уравнения движения идеальной жидкости , их интегрирование. Уравнение Бернулли для элементарной струйки жидкости.
- •14.Распространение ур-я Бернули для струйки на поток жидкости.
- •15. Геометрическая и энергетическая интерпритация ур-я Бер-и для потока реальной жид-ти.
- •16.Общие сведенья о потере напора.Режимы движ-я жид-ти.Осн-е ур-я равномерного движ-я жид-т.
- •17.Распред-е скоростей в сечении потока,потери напора по длине при ламинарном движ-и,потеря давления.
- •18.Общие сведенья о турбулентном потоке.
- •19.Зоны сопротивления движ-ю жид-ти.
- •20.Коэф-т гидравлического трения.Ф-лы для его опр-я.
- •21.Потеря напоро по длине при тур-ом движ-и. Ф-ла шези,ее практическое использование.Потеря давления по длине.
- •Формула Шези имеет вид
- •22.Местные потери напора и местные потери давления.
- •23.Истечение жидкостей через отверстия и насадки – основные задачи и их решения.
- •24.Равномерное движение воды в каналах, задачи при расчете каналов, их решение расчет каналов замкнутого поперечного сечения.
- •25.Установившееся неравномерное движ-е жид-тив водотоках.Задачи и их решение. Расчет кривой свободной пов-ти воды.
- •26. Расчет и построение кривой свободной поверхности воды в естественных водотоках.
- •27. Гидравлический прыжок – основные задачи расчетов, их решение.
6.Основные уравнения гидростатики(оуг), его геометрическая и энергетическая интерпретация.
Основным законом (уравнением) гидростатики называется уравнение
![]() ,
,
где
![]() —
гидростатическое
давление (абсолютное или
избыточное) в произвольной точке
жидкости,
—
гидростатическое
давление (абсолютное или
избыточное) в произвольной точке
жидкости,
![]() — плотность жидкости,
— плотность жидкости,
![]() — ускорение
свободного падения,
— ускорение
свободного падения,
![]() —
высота
точки над плоскостью сравнения
(геометрический напор]),
—
высота
точки над плоскостью сравнения
(геометрический напор]),
![]() —
гидростатический напор].
—
гидростатический напор].
Уравнение показывает, что гидростатический напор во всех точках покоящейся жидкости является постоянной величиной.
Иногда основным законом гидростатики называют принцип Паскаля[4].
Основное уравнение гидродинамики имеет геометрический и физический смысл:
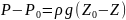
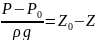
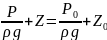
Каждое полученное слагаемое имеет линейное значение, поэтому ОУГ имеет геометрический и физический смысл.
Геометрический заключается в следующем:
 -
геометрический
напор
-
геометрический
напор
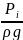 – Пьезометрический
напор
– Пьезометрический
напор
Физический смысл гидростатики заключается – это уравнение показывает запас потонциальной энергии , которое обладает рассматриваемый объем житкости.
7.Силы гидростатического давления действующие на плоские поверхности конечного размера.

На
плоской поверхности
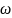 выбираем элементарную площадку
выбираем элементарную площадку
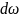 и определим силу
и определим силу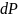 действующую на эту площадку
действующую на эту площадку
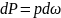 тарную
площадку
,
которое опре
тарную
площадку
,
которое опре
Где P – давление на элемеделяется по основному закону кинематики
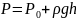 .
.
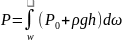 =
=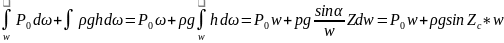
H=Z*sina
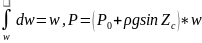 ,
,
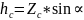
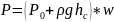
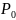 -внешнее
давление,
-внешнее
давление,
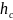 – Глубина погружения центра тяжести,
w-
площадь поверхности плоскй.
– Глубина погружения центра тяжести,
w-
площадь поверхности плоскй.
Если
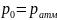 не учитывается
не учитывается
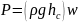
Если
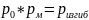

Если
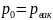

8.Определение центра избыточного давления.
Центр давления силы атмосферного давления p0S будет находиться в центре тяжести площадки, поскольку атмосферное давление передаётся на все точки жидкости одинаково. Центр давления самой жидкости на площадку можно определить из теоремы о моменте равнодействующей силы. Момент равнодействующей
силы относительно оси ОХ будет равен сумме моментов составляющих сил относительно этой же оси.
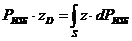 ,
откуда
,
откуда 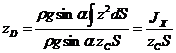 где:
где: ![]() -
положение центра
избыточного давления на вертикальной
оси,
-
положение центра
избыточного давления на вертикальной
оси, ![]() -
момент инерции площадки S относительно
оси ОХ.
-
момент инерции площадки S относительно
оси ОХ.
Центр давления (точка приложения равнодействующей силы избыточного давления) расположен всегда ниже центра тяжести площадки. В случаях, когда внешней действующей силой на свободную поверхность жидкости является сила атмосферного давления, то на стенку сосуда будут одновременно действовать две одинаковые по величине и противоположные по направлению силы обусловленные атмосферным давлением (на внутреннюю и внешнюю стороны стенки). По этой причине реальной действующей несбалансированной силой остаётся сила избыточного давления.
При расчете конструкций, воспринимающих давление жидкости необходимо знать не только силу давления, но и точку ее приложения. Попробуем предположить, что результирующая сила давления приложена в геометрическом центре.
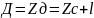 ,
где
,
где
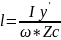
9. Силы гидростатического давления действующие на криволинейные поверхности.
Давление жидкости на цилиндрическую поверхность.Пусть жидкость заполняет резервуар, правая стенка которого представляет собой цилиндрическую криволинейную поверхность АВС (рис.2.2), простирающуюся в направлении читателя на ширину b. Восстановим из точки А перпендикуляр АО к свободной поверхности жидкости. Объем жидкости в отсеке АОСВ находится в равновесии. Это значит, что силы, действующие на поверхности выделенного объема V, и силы веса взаимно уравновешиваются.

Представим, что выделенный объем V представляет собой твердое тело того же удельного веса, что и жидкость (этот объем на рис.2.2 заштрихован). Этот объем называется телом давления. Левая поверхность этого объема (на чертеже вертикальная стенка АО) имеет площадь Sx = bH, являющуюся проекцией криволинейной поверхности АВС на плоскость yOz.Cила гидростатического давления на площадь Sx равна Fx = γSxhc.С правой стороны на отсек будет действовать реакция R цилиндрической поверхности. Пусть точка приложения и направление этой реакции будут таковы, как показано на рис.2.2. Реакцию R разложим на две составляющие Rx и Rz.Из действующих поверхностных сил осталось учесть только давление на свободной поверхности Р0. Если резервуар открыт, то естественно, что давление Р0 одинаково со всех сторон и поэтому взаимно уравновешивается.На отсек АВСО будет действовать сила собственного веса G = γV, направленная вниз.Спроецируем все силы на ось Ох:
Fx - Rx = 0 откуда Fx = Rx = γSxhc
Таким образом, вертикальная составляющая давления жидкости на криволинейную поверхность равна весу жидкости в объеме тела давления.Составляющая силы гидростатического давления по оси Oу обращается в нуль, значит Ry = Fy = 0.Таким образом, реакция цилиндрической поверхности в общем случае равна
![]()
а поскольку реакция цилиндрической поверхности равна равнодействующей гидростатического давления R=F, то делаем вывод, что
![]()
Направление
силы давления по отношению к горизонту
жидкости определяется углом ![]() ,
причем
,
причем ![]() .
.
