Понятие об условной вероятности
Если при вычислении р(А) на него не накладывается никаких других условий, кроме комплекса условий Q, то такая вероятность будет безусловной, но часто р(А) нужно найти при условии, что событие В произошло. Такие вероятности называются условными р(А/В) или рВ(А).
П
усть
событию В
благоприятствует k
возможных результатов, а событию АВ
r
возможных результатов испытаний. Пусть
В
произошло. А
может произойти только тогда, когда
осуществится одно из r
возможных результатов.
,
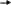где n
– общее число возможных результатов.
Аналогично рассуждая можно получить
условную вероятность наступления В:
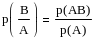
Из этих формул
можно получить теорему умножения
вероятностей:
Вероятность произведения двух событий равна произведению вероятности одного из этих событий на условную вероятность другого события при условии, что первое событие произошло. Для независимых событий: p(AB)=p(A)∙p(B) – вероятность произведения равна произведению вероятностей. Пусть В может произойти вместе с одним из событий А1,А2, …, Аn, причем ВАi и BAj, i≠j. В реализуется с Аi. При этом:
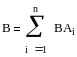
В соответствии с теоремой умножения вероятностей можно получить формулу полной вероятности.
Теорема Байеса
Пусть В может произойти в результате осуществления одной из гипотез А1,А2, …, Аn. Гипотеза – это одно из несовместимых событий полной группы. Пусть известны вероятности этих гипотез р(А1), р(А2), …, р(Аn). Известны вероятности событий по этим гипотезам р(В/А1), р(В/А2), …, р(В/Аn). Такие вероятности называются априорными. Пусть испытание произошло. В результате можно переоценить вероятность гипотез, так как известно событие, в результате которого появилось В. Такая вероятность называется апостериорной.
Эта переоценка реализуется по формуле Байеса:
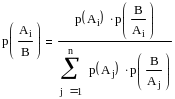
Если вероятность событий по каждой из гипотез В/Аi считается одинаковой и равной: 1/n, то можно значительно упростить формулу. Тогда апостериорные вероятности гипотез пропорциональны вероятностям событий по каждой гипотезе.
Случайные величины и их законы распределения
Если рассматривать генеральную совокупность, то представление о ней дат выборочная совокупность или выборка. Любой изучающий признак выборки является случайной величиной, но не всякая случайная величина является признаком. Признак – это переменная величина которая может принимать то или иное значение в результате опытов. Такие величины называются случайными. Любое непрерывное значение случайной величины называется её возможным значением. В выборке случайная величина принимает не все значения, а некоторое конечное число этих значений, то есть вариантов. Следует отличать вариант, или элемент выборки, от возможного значения случайной величины. Выборка может не охватывать всех возможных значений. Все множество признаков в соответствии с теорией множеств можно разделить на две группы:
Определяемые на дискретных множествах: список.
Определяемые на непрерывных множествах, то есть задание интервалами или неравенствами. Случайные величины имеет свой закон распределения. Для случайных величин закон распределения можно задать в виде таблицы соответствия между ее возможными значениями и их вероятностями
x |
x1 |
x2 |
… |
xn-1 |
xn |
p(x) |
p(x1) |
p(x2) |
… |
p(xn-1) |
p(xn) |
Так как события, состоящие в том, что дискретная случайная величина примет возможное значение, являются несовместимыми, то они образуют полную группу, а значит:
.
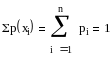Cуществует графическая интерпретация закона распределения, которая может быть представлена многоугольником распределения.
p
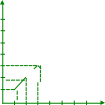
x
Механическая интерпретация закона распределения – это распределение веса (массы) равного единице в точках x1, x2, …, xn.
Пример: пусть дискретной случайной величиной будет количество дефекта при контроле 3 деталей. Построить ряд распределения и многоугольник распределения.
х0 – событие, состоящее в том, что ни одна деталь не дефектна
х1 – событие, состоящее в том, что одна деталь дефектна
х2 – событие, состоящее в том, что две детали дефектны
х3 – событие, состоящее в том, что три детали дефектны
x |
x0 |
x1 |
x2 |
x3 |
p(x) |
0,125 |
0,375 |
0,375 |
0,125 |
p(x)=m/n
p(x0)=1/8=0,125
p(x1)=3/8=0,375
p(x2)=3/8=0,375
p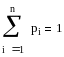
(x3)=1/8=0,125
Поле исходов: 8 исходов. От нуля изделий до трех.
Для непрерывной случайной величины задание таблицей неприемлемо, так как: во-первых, нельзя перечислить все возможные значения случайной величины; во-вторых, вероятность каждого возможного значения равна нулю. Существует универсальная форма задания закона распределения, которая пригодна и для непрерывных случайных величин и для дискретных случайных величин. Закон распределения модно задать функцией распределения F(x) – это вероятность того, что случайная величина x примет значение меньше некоторого текущего значения: F(x)=p(X<x). Это интегральный закон распределения, а F(x) – интегральная функция распределения. В соответствии со свойствами F(x) непрерывная случайная величина – это случайная величина, интегральная функция которой непрерывно дифференцируема.