Содержание

1. Введение

2. Основные аксиомы теории вероятностей, или аксиоматика Колмогорова (1903 – 1987)

3. Аксиомы, определяющие вероятность

4. Законы тождества

5. Определения вероятности

6. Понятие об условной вероятности

7. Теорема Байеса

8. Случайные величины и их законы распределения

9. Свойства функции распределения

10. Плотность распределения

1. Свойства плотности распределения

11. Числовые характеристики случайных величин

1. Математическое ожидание числа появления события в одном опыте. Закон распределения

2. Свойства математического ожидания

12. Характеристики рассеяния

1. Свойства дисперсии

13. Стандартные распределения дискретных случайных величин

14. Проверка статистических гипотез

15. Алгоритм проверки статистических гипотез

16. Стандартные распределения непрерывных случайных величин

17. Этапы моделирования непрерывных случайных величин

18. Локальная и интегральная теоремы Лапласа

19. Система случайных величин

20. Интегральная F(x)

21. Дифференциальная f(x) для непрерывных двумерных случайных величин

22. Моменты двумерной выборки

23. Центральная предельная теорема

24. Метод статистических испытаний, или метод Монте-Карло

25. Задача «о случайном блуждании»

26. Статистические оценки параметров распределения случайных величин

27. Доверительные границы

28. β- и γ- распределения и функции

29. χ²-распределение или распределение Пирсона

1. Плотность χ²-распределения

29. Распределение Стьюдента (Госсета), или t-распределение

30. Распределение Фишера, или f-распределение. Модели дисперсионного анализа

31. 1. Однофакторный дисперсионный анализ

    2. Двухфакторный дисперсионный анализ

32. Модели непараметрической статистики

33. Краткие выводы по курсу

Введение

Первые работы по теории вероятностей были выполнены в 16 веке, в частности, итальянскими математиками. Тарталья составил таблицу количества очков при бросании игральных костей, то есть анализировалось количество исходов. Кардано в работе «Об азартной игре» дал оценку вероятностей этих событий. Галилей создал основы комбинаторики, а также составил таблицу смертности, где указал вероятную продолжительность жизни. В начале 18 века была опубликована работа Иакова Бернулли (1654-1705), где было дано математическое обоснование закона больших чисел. Бернулли доказал, что многократная реализация совокупности одних и тех же событий при неизменных внешних условиях (в комплексе внешних условий Q) приводит к устойчивой вероятности этих событий. Вероятность – это степень уверенности в наступлении того или иного события. Вероятность рассматривается в рамках поля исходов. Наблюдения рассматриваются в рамках. В отличие от опыта испытание может происходить без наблюдателя. Любые явления можно считать испытаниями, если в них реализуются одни и те же условия. События являются результатом испытаний. Событие – это любая ситуация, которую можно наблюдать, и которая может возникнуть в результате опыта. Теория вероятностей – это математическая наука о закономерностях случайных величин. Теория вероятностей – это наука, где все исходы можно предусмотреть. Во многих случаях информацию можно получить, не зная данных обо всей предметной области (генеральной совокупности). Тогда наблюдения проводят за выборочной совокупностью, или выборкой. Выборочный метод – это основа математической статистики, или науки о закономерностях и методах изучения массовых явлений. Впервые массовые наблюдения в России были проведены в 70^е годы 19 века. В 1901 году Борткевич доказал, что теоретической основой выборочного метода является исчисление вероятностей. В 1906 году английский статистик Боули показал методику определения случайных ошибок выборочного наблюдения. Любая выборка изучается по какому-либо признаку. Признак – это то или иное свойство, присущее всем элементам статистической совокупности. Признаки могут быть количественными и качественными. Количественные – измеряемые признаки. Качественные могут существовать или отсутствовать. Количественные признаки называются параметрами и могут менять свое значение, то есть варьировать.

Те или иные выводы можно получить, используя различные виды отбора:

• это отбор без разбиения генеральной совокупности на части – простой случайный бесповторный отбор,

• простой случайный повторный отбор,

• отбор, требующий разбиения генеральной совокупности:

• типический отбор

• механический

• серийный отбор.

• объекты отбираются из каждой «типической» части, где признак заметно варьирует (оборудование различного типа, студенты разных лет обучения).

• общая совокупность механически делится на столько групп, сколько объектов должно войти в выборку и из каждой группы отбирается один объект.

• объекты отбираются сериями, которые подвергаются сплошному обследованию (методики сплошного контроля). Здесь наблюдаемый признак колеблется незначительно.

На практике реализуются схемы комбинированного отбора. Например, общая совокупность разбивается на серии одинакового объема. Далее простым случайным отбором выбираются несколько серий. Затем простым случайным отбором извлекаются отдельные объекты. Кроме способов отбора характеристики выборки зависят от объема выборки, то есть от количества ее элементов.

Основные аксиомы теории вероятностей, или аксиоматика Колмогорова (1903 – 1987)

Случайные события, исход которых будет известен тогда, когда оно произойдет, не является первичным понятием, а определяется через более простые понятия. Пусть существует пространство событий U. Далее строится система событий F, в которую включаются всевозможные подмножества из U. Элементы F называются случайными событиями. К F предъявляется два требования:

• В F как элемент включается U.

• Если в F входят события А и В, то элементами F будут события А+В, АВ, Ā, .

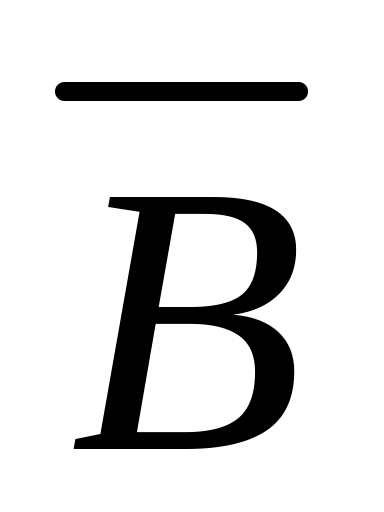Если система удовлетворяет двум этим требованиям, то поле событий назевается булевским (Дж. Буль, 1815 – 1864). Сумма событий – это новое событие, состоящее в наступлении хотя бы одного из исходных событий. Произведение событий, то есть новое событие, состоит в наступлении обоих событий. Отрицание – противоположное событие. Разностью событий называется событие, состоящее в наступлении события А и ненаступления события В.

Существует понятие, что одно событие (например, А) влечет за собой другое событие (например, В). А‹В, В›А.

Выделяется достоверное событие U=A+Ā, которое неизбежно произойдет в результате каждого испытания. Другим событием является невозможное событие, которое никогда не может произойти. События A и В являются несовместимыми, если их совместное появление невозможно (V=AĀ, V=AB).

Если событие А представлено суммой попарно несовместимых событий A=B₁+B₂+…+B_n. B_iB_j=V, то событие А подразделяется на частные случаи. B₁+B₂+…+B_n=U, то B₁, B₂, …, B_n образуют полную группу событий.

Таким образом, в системе двух событий А и В элементами системы являются (А+В, АВ, А-В), а также U и V, то есть система является полем событий.

Если добавляется ещё одно событие, если A₁+A₂+…+A_n являются элементами F, то F будут A₁+A₂+…+A_n и A₁*A₂*…*A_n тогда система F будет называться Гореловым полем событий. Если А и В не содержат в своём составе одинаковых элементов из множества событий то F cодержит в своём составе S в качестве элементов по F должно содержать , или пустое множество, или не возможное событие. Таким образом элементарные действия над событиями не выводят математиков за пределы системы случайных событий F.