14. Уравнение движения машинного агрегата в энергетической и дифференциальной формах.

В результате приведения сил и масс реальную схему механизма заменяют упрощенной динамической моделью с вращающимся или поступательным звеном приведения

Уравнение движения показывает зависимость силовых параметров M_n (или F_n) от инерционных I_n (m_n) или кинематических q, V или w, a или 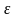. Уравнение движения может записываться в дифференциальной или интегральной формах.

Уравнение в дифференциальной форме основано на равенстве дифференциалов элементарных работ dA и дифференциалов кинетической энергии dT в любой момент времени: dA=dT.

Покажем для вращающегося звена приведения:

; ; ;

;

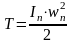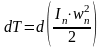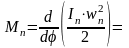
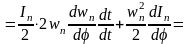
Аналогично можно получить для поступательного звена приведения

26.Кпд при последовательном и параллельном соединении механизмов.

КПД называется отношение абсолютной величины работы сил полезных (производственных) – сопротивлений к работе движущих сил А_дв за полный цикл уста­новившегося движения

η=

К.П.Д. — один из основных критериев, характеризую­щих степень механического совершенства машины. Он показывает, какая часть подводимой к машине энергии используется по прямому назначению, т. е. затрачивается на выполнение определенного технологического процесса. Остальная энергия расходуется на преодоление вредных сопротивлений (сил трения, сил сопротивления окружаю­щей среды и пр.). Следовательно,

(2)

-работа сил вредных сопротивлений. С учетом зависимости (2) формула (1) принимает вид:

К.п.д. зависит от выбора схемы механизма и его конструктивного выполнения, качества изготовления и монтажа, смазки и т. п. Кроме того, к.п.д. одной и той же ма­шины зависит также от режима ее работы — скорости и нагрузки. С возрастанием полезной нагрузки от нуля (холостой ход) до максимальной величины к.п.д. сначала возрастает от нуля до максимума (оптимальный режим)., а затем уменьшается. Для каждой машины существует также наивыгоднейшая скорость, при которой к.п.д. до­стигает максимума.

Изменение к.п.д. машины в зависимости от режима ее работы затрудняет определение его расчетным путем. По­этому при расчетах обычно учитывается зависимость к.п.д. машины только от к.п.д. отдельных ее частей (меха­низмов, передач, кинематических пар) и от способа их соединения. Для многих кинематических пар и некото­рых простейших механизмов разработаны аналитические методы определения к.п.д. В некоторых случаях поль­зуются практически установленными средними значения­ми к.п.д.

Если п механизмов соединены последовательно и из­вестны к.п.д. каждого механизма - то об­ щий к.п.д. определяется по формуле

ŋ=ŋ₁ŋ₂ŋ₃…ŋ_n

η=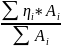

Если отдельные механизмы включены параллельно ,и к каждому из них подводится соответственно работа 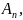то общий к.п.д. равен

Общий к.п.д. смешанного соединения определяется путем совместного использования формул последовательного и параллельного соединений.

Все приведенные выше зависимости имеют смысл только для установившегося движения машины. Причем, если установившееся движение периодическое, то к.п.д. определяется как отношение работ, производимых сила­ми за время одного или нескольких циклов работы ма­шины.