37. Линейные преобразования в арифметических-мерных пространствах.

Отображение векторного пространства называется линейным оператором, если для любых векторов , и для любого числа выполняются условия:

1) ;

2) .

Теорема 2. Всякий линейный оператор однозначно определяется некоторой матрицей .

Выразим векторы через векторы базиса .

Обозначим

,

Тогда

Отсюда .

Таким образом, действие оператора на произвольный вектор

полностью определяется умножением координатной строки вектора на матрицу .

38. Собственные векторы.

Собственным вектором линейного преобразования (или соответствующей матрицы ) называется такой вектор , что . Число называется собственным значением оператора для вектора . После линейного преобразования векторы и являются коллинеарными.

Пусть для некоторого собственного вектора и собственного значения . Тогда , или . Так как , то . Последнее уравнение называется характеристическим.

Пример 3. Найти все собственные значения и собственные векторы линейного преобразования пространства имеющего матрицу

Решение. Составим характеристическое уравнение .

В нашем случае

.

Откуда , и .

Случай 1. . Тогда для собственного вектора получим матричное равенство , или

Перемножая матрицы слева и сравнивая элементы, получим систему

которая равносильна уравнению с двумя неизвестными .

39. Модель международной торговли.

Соврем. факты в мировой эк-ке свидетельствуют о след. направлениях в международной торговле:

· росте торговли интеллектуалоемкими товарами;

· сближении торговли между индустриальными странами;

· росте внутриотраслевой торговли (импорта и экспорта) между странами.

Стандартная модель расширила круг до совокупного спроса и предложения. Для простоты понимается, что существуют две страны(1 и 2) И два товара (А и В). Модель сравнительных преимуществ рассматривала ситуацию в условиях постоянных издержек замещения (т.е. для производства дополнительной единицы товара А надо пожертвовать постоянным количеством товара Б). Это означало ситуацию полной специализации стран на товарах своего относительного преимущества. Стандартная модель исходит из предпосылки о растущих издержках замещения, закономерности, известной из общей экономической теории и более соответствующей существующим экономическим реалиям.

40. Квадратичные формы и их преобразования методом Лагранжа.

Квадратичной формой от переменных называется однородный многочлен второй степени от этих переменных. В общем виде квадратичную форму можно записать как

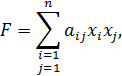
где – матрица квадратичной формы. Если обозначить через , то квадратичная форма будет иметь вид .

Алгоритм Лагранжа. с матрицей

Если хотя бы один из диагональных элементов , то делается переход к новым переменным: и для . В результате получим квадратичную форму относительно переменных , в которой не будет смешанных произведений переменных, содержащих . Если все коэффициенты матрицы вида равны нулю, то для какого –

нибудь слагаемого делается переход к новым переменным по формулам и для и . В результате в квадратичной форме появятся квадраты переменных и можно будет исключать из смешанных переменных либо , либо .