
- •Вопросы к экзамену по высшей математике.
- •Декартова и полярная системы координат.
- •Расстояние между двумя точками на плоскости.
- •Общее уравнение прямой на плоскости.
- •Гипербола.
- •Парабола.
- •Матрицы и их виды.
- •Умножение матриц и его свойства.
- •Элементарные преобразования матриц.
- •Ранг матрицы.
- •Определители 2-го и 3-го порядков.
- •Обратная матрица и ее свойства.
- •Вычисление обратной матрицы с помощью элементарных преобразований.
- •Теорема Кронекера - Копелли.
- •Правило Крамера.
- •Метод Гаусса.
- •Метод обратной матрицы.
- •31. Векторы и линейные операции над ними.
- •Линейные операции над векторами.
- •32. Скалярное произведение векторов и его свойства.
- •33. Векторное произведение векторов и его свойства.
- •34. Смешанное произведение векторов и его свойства.
- •35. Арифметические - мерные векторные пространства и их примеры.
- •36. Базис векторного пространства, примеры.
- •37. Линейные преобразования в арифметических-мерных пространствах.
- •38. Собственные векторы.
- •39. Модель международной торговли.
- •40. Квадратичные формы и их преобразования методом Лагранжа.
- •41. Знакопостоянные квадратичные формы. Критерий Сильвестра.
- •42. Функции и методы их задания, свойства: четность, периодичность, монотонность.
- •43. Предел функции и его свойства.
- •44. Бесконечно малые и беск.Большие функции.
- •45. Связь между пределом и бесконечно малыми фун-ми.
- •52. Точки разрыва первого рода
- •53. Точки разрыва второго рода.
- •54. Признаки существования функций.
- •55. Элементарные функции и их непрерывность.
- •56. Производная функции и ее геометрический, физический и экономический смысл.
- •57. Связь между непрерывностью и дифференцируемостью функций.
- •64. 65. Понятие дифференциала функции
- •66. Применение дифференциала в приближенных вычислениях
- •67. Производные и дифференциалы высших порядков
- •Порядок исследования иногда целесообразно выбирать исходя из конкретных особенностей данной функции. 77. Формулы Маклорена и Тейлора
- •78. А.Функции нескольких переменныхОсновные понятия.
- •79. В.Частные производные первого порядка.
- •82.Экстремум функции двух переменных.
- •85 Комплексные числа.
- •86. Форма записи комплексного числа
- •87. Формула Муавра и извлечение корней из комплексных чисел
- •90.В.Таблица основных неопределённых интегралов.
- •91,92. В.Понятие об основных методах интегрирования.
Элементарные преобразования матриц.
Элементарными преобразованиями матриц являются:
Перестановка местами двух любых её строк (столбцов).
Умножение элементов какой-нибудь строки (столбца) на некоторое не нулевое число.
Прибавление ко всем элементам строки (столбца) соответствующих элементов другой строки (столбца), умноженных на одно и то же число.
Две
матрицы ![]() называются эквивалентными,
если одна из них получается из другой
с помощью элементарных преобразований
называются эквивалентными,
если одна из них получается из другой
с помощью элементарных преобразований![]()
Любую матрицу с помощью элементарных преобразований можно привести к ступенчатому виду.
________________________________________________________________________
Ранг матрицы.
Пусть дана матрица размерности ![]()

Выделим в ней ![]() строк
и
столбцов.
строк
и
столбцов.
![]() .
Из элементов, стоящих на пересечении
строк
и
столбцов
составим определитель
– го порядка. Все такие о Минор, порядок
которого равен рангу матрицы, называют
базисным минором. У каждой матрицы
может быть несколько базисных миноров.
.
Из элементов, стоящих на пересечении
строк
и
столбцов
составим определитель
– го порядка. Все такие о Минор, порядок
которого равен рангу матрицы, называют
базисным минором. У каждой матрицы
может быть несколько базисных миноров.
Свойства ранга матрицы.
1. При транспонировании матрицы её ранг не меняется.
2. Если из матрицы убрать нулевую строку (нулевой столбец), то ранг матрицы не изменится.
3. Ранг матрицы не меняется при её элементарных преобразованиях.
4. Ранг матрицы равен числу не нулевых строк в её ступенчатом виде.
пределители называют минорами матрицы.
_____________________________________________________________
Определители 2-го и 3-го порядков.
Определитель - квадратная числовая таблица, вычисляемая по определенным правилам.
Если
 ,
то
,
то  . Так
. Так 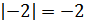 .
.Если
 ,
то
,
то  .
.
Так ![]() .
.
Если
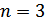 ,
то
,
то

![]() .
Так
.
Так
 .
.
 При вычислении
определителей 3-го порядка удобно
пользоваться правилом треугольников.
С плюсом берутся произведения элементов
стоящих на главной диагонали и элементы,
стоящие в вершинах следующих треугольников.
При вычислении
определителей 3-го порядка удобно
пользоваться правилом треугольников.
С плюсом берутся произведения элементов
стоящих на главной диагонали и элементы,
стоящие в вершинах следующих треугольников.

С минусом берутся произведения элементов, стоящих на второй диагонали и в вершинах следующих треугольников.

Второй метод заключается в том, что рядом с определителем справа записываются первый и второй столбцы и тогда с плюсом берутся произведения элементов, стоящих на главной диагонали и двух ей параллельных, с минусом – произведения элементов, стоящих на второй диагонали и двух ей параллельных.
_________________________________________________________
Определитель n – го порядка.
Вычисление определителей более высоких порядков осуществляется путем использования их свойств.
ОБЩИЙ ПОДХОД: опред-ль = сумме произведений элементов какой-либо строки(столбца) на их алгебраические дополнения
_______________________________________________________________________
Алгебраические дополнения.
Алгебраическим
дополнением
элемента
![]() определителя называют число
определителя называют число ![]() .
Например
.
Например
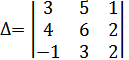 ,
,
![]() .
.
_________________________________________________________________________
Вычисление определителей разложением по элементам строки или столбца.
!!!!!!!!!!!!!!!!
Свойства определителей.
Свойства определителей.
1. Определитель не изменится, если
его строки заменить столбцами и наоборот,
т. е. ![]() .
.
2. Определитель меняет знак при перестановке любых двух его строк (столбцов).
3. Определитель, имеющий две равные строки (столбца), равен 0.
4. Общий множитель строки (столбца) можно выносить за знак определителя, например
![]() .
.
5. Если элементы какой-нибудь строки (столбца) представимы в виде суммы двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, например

6. Определитель не изменится, если к какой-нибудь строке (столбцу) прибавить соответствующие элементы другой строки (столбца), умноженные на некоторое ненулевое число.
 (I=I+II).
(I=I+II).
7. Определитель треугольной матрицы равен произведению её диагональных элементов.
8. Определитель равен сумме произведений элементов какой-нибудь его строки (столбца) на их алгебраические дополнения. Например
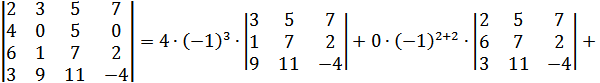
 .
.
Для вычисления определителя мы использовали разложение по второй строке, так как она содержит большее число нулевых элементов.
9. Сумма произведений элементов какой-нибудь строки (столбца) на соответствующее алгебраическое дополнение другой строки (столбца) равна 0.
___________________________________________________________________
