Вопросы к экзамену по высшей математике.

1. Декартова и полярная системы координат.

Декартова система координат - пара взаимно перпендикулярных прямых с заданными направлением и масштабом. Вертикальная прямая – ось (ось ординат); горизонтальная – ось (ось абсцисс). Каждая точка на плоскости определяется двумя числами , (рис. 1), называемыми координатами .

Полярная система координат состоит из точки которая называется полюсом, и оси, задающей некоторое первоначальное направление. Оно совпадает с направлением оси Положение любой точки определяется расстоянием от неё до полюса и углом между прямой, содержащей точку и проходящей через полюс, и первоначальным направлением

___________________________________________________________________________

2. Расстояние между двумя точками на плоскости.

Пусть в декартовой системе координат даны две точки и (рис. 5). Тогда расстояние можно найти по формуле

.

________________________________________________________________________________

3. Д еление отрезка в данном отношении.

Пусть в декартовой системе координат даны две точки - и (рис. 6). Координаты точки отрезка , такой, что находятся по формулам

_______________________________________________________________________________

4. Уравнение прямой, проходящей через данную точку.

У равнение прямой через угловой коэффициент имеет вид где , - угол наклона прямой с положительным направлением оси - точка пересечения прямой с осью (рис.8).

5. У равнение прямой, проходящей через две точки.

Пусть дана точка с координатами . Тогда уравнение прямой, проходящей через точку и имеющей угловой коэффициент (рис. 11) имеет вид

__________________________________________________________________________

6. У гол между двумя прямыми.

Пусть заданы две прямые и (рис. 17). Тогда

, , и угол между этими прямыми можно вычислить по формуле откуда

___________________________________________________________________________

7. Условия параллельности и перпендикулярности двух прямых.

• Условие параллельности

Е сли две прямые и параллельны, то угол между ними равен нулю и тогда Следовательно, , или .

• Условие перпендикулярности

Е сли две прямые и взаимно перпендикулярны (рис. 19), то угол между ними равен и не существует. А так как и дробь

не существует тогда и только тогда, когда её знаменатель равен нулю, т.е. тогда, когда выполняется равенство . Это и есть условие перпендикулярности двух прямых. Выразив один угловой коэффициент через другой, получим

8. Общее уравнение прямой на плоскости.

Уравнение вида называется общим уравнением прямой.

а) Если , то уравнение будет иметь вид . Прямая, определяемая этим уравнением, проходит через начало координат, так как координаты удовлетворяют этому уравнению.

б) Если , то уравнение примет вид или

Уравнение не содержит переменной , а определяемая этим уравнением прямая, параллельна оси .

в) Если , то уравнение примет вид , откуда

Обозначим

получим - уравнение прямой через угловой коэффициент .

___________________________________________________________________________

9. Уравнение прямой в отрезках по осям.

Пусть график некоторой прямой отсекает на осях и отрезки и соответственно (рис. 15). Тогда уравнение прямой имеет вид

__________________________________________________________________________

10. Нормальное уравнение прямой.

Если - расстояние от полюса до прямой, то уравнение прямой вида называется нормальным (рис. 21).

Замечание. Чтобы общее уравнение прямой записать в нормальном виде необходимо его разделить на выражение и заменить

________________________________________________________________

11. Р асстояние от точки до прямой.

Пусть дано общее уравнение прямой и дана точка , не лежащая на прямой. Тогда расстояние от точки до этой прямой (рис. 22) вычисляется по формуле

12. Уравнение прямой в полярной системе координат.

Пусть дана система полярных координат с полюсом в точке и прямая, проходящая на расстоянии от полюса (рис. 20). Тогда уравнение прямой будет иметь вид

______________________________________________________________________

13. Окружность и эллипс.

• Окружность с центром в точке 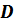радиуса 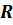- множество всех точек плоскости, удаленных от точки на расстояние .

Если центр окружности имеет координаты (рис. 1), то каноническое уравнение окружности имеет вид

Если , то центр окружности находится в начале координат и каноническое уравнение имеет вид

• Эллипс.

Эллипс - множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.

Если фокусы эллипса и , лежат на оси (рис. 2), то каноническое уравнение имеет вид

Если , то эллипс превращается в окружность . Числа и называются большой и малой осями эллипса. Величина ( , если называется эксцентриситетом эллипса. У эллипса всегда . Если , (случай окружности) то , следовательно, и . Если , то фокусы эллипса расположены на оси (рис. 3). Прямые ( , если ) называются директрисами эллипса (рис. 4).