22) Поля и формы в пространстве.
Если
– дуальный базис по отношению к
,
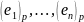то:
.
Эта функция называется дифференциальной
формой. Векторное поле – это функция
,
которая каждой точке
ставит в соответствие вектор
.
Если
– значение векторного поля, то оно
определяется:
,
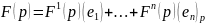где
–координатные
функции поля.Пусть задано дифференцируемое
отображение
.
Тогда определено линейное преобразование:
;
В свою очередь, это линейное отображение
индуцирует линейное отображение:
,
которое определяется следующим образом:
.
Здесь,
,
а
–
любые векторы из пространства
.
Вышеуказанная формула называется
формулой переноса дифференциальных
форм. Она представляет собой вариант
формулы замены переменной. При этом,
функция
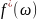называется прообразом дифференциальной
формы
.
Следующая теорема описывает свойства
отображения
.
Теорема
19.1: Пусть
отображение
–
дифференцируемо. И пусть
- скалярная функция. Тогда: 1)
;
2)
;
3)
;
4)
.
Док-во:
Пусть
.
.
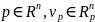Поскольку
– любой, равенство доказано. Остальные
пункты доказываются аналогично.
Теорема доказана.
23) Потенциал.
Теорема
20.1: Для
операции дифференцирования форм
определены свойства: 1)
;
2) Если
– форма
-й
степени, то дифференциал
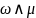равен:
;
3)
.Коротко:
;
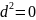4)
где:
– дифференцируемая функция, а
– форма в пространстве
.
Док-во:
Первый пункт очевиден. Второй пункт
очевиден если
–скалярная
функция. Также, равенство очевидно для
формы вида:
;
Рассмотрим форму:
;
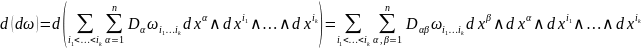; Для
имеем 2 слагаемых:
;
.
Эти два слагаемых отличаются лишь знаком
и в сумме дают 0, поэтому и вся сумма
равна нулю. Последний пункт доказывается
индукцией по степени дифференциальной
формы. Для формы 0-й степени это сделать
нетрудно. Предположим, что утверждение
верно для любой формы
-й
степени. Индуктивный переход достаточно
сделать для формы
,
где
–форма
-й
степени:
.
Теорема
доказана.
Также дадим определения: 1)Форма
называется замкнутой если
.
2) Форма
называется точной если существует такая
форма
,
что
.
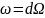3)
называется
потенциалом или первообразной для
.
Лемма Пуанкаре (20.1): Если
– замкнутая форма на открытом звездном
относительно начала координат множестве,
то она точна на этом множестве.
24) Теорема Стокса.
Теорема
Стокса(22.1):
Пусть
– форма
-й
степени на
,
и
–
-мерная
сингулярная цепь в
.
Тогда:
.
Док-во:
Предположим, что
.
Форма
-й
степени состоит из суммы форм вида:
;
Достаточно доказать теорему Стокса для
этих форм. Для этого заметим:
; Рассмотрим:
; Далее, рассмотрим:
; Теперь, к последнему интегралу применим
теорему Фубини и формулу Ньютона-Лейбница:
.
Как следствие, получаем равенство:
.
Теорема Стокса доказана для стандартного
-мерного
куба. Пусть теперь
-произвольный
сингулярный
-мерный
куб. Тогда:
.
Теорема доказана для произвольного
сингулярного куба. Пусть теперь
– произвольная сингулярная цепь:
;
.
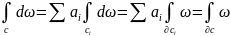Теорема доказана.
25) Поверхности.
Пусть
– открытые множества в
.
Дифференцируемое отображение
,
имеющее дифференцируемое обратное
отображение, называется диффеоморфизмом.
Подмножество
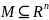называется
-мерной
поверхностью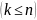
в
(
-мерным
многообразием), если выполняется
следующее условие: Для любой точки
существуют открытые множества
и диффеоморфизм
,
обладающий свойством:
.
Фактически, это означает, что
является частью пространства
.
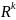Теорема
22.3: Для каждой
точки
-мерной
поверхности
,
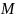выполняется следующее «координатное
условие»: Существует открытое множество
и открытое множество
,
а также, дифференцируемое взаимно-однозначное
отображение
,
для которого имеют место два свойства:
;
;
Функция
называется системой координат в
окрестности точки
.
Док-во:
Будем действовать в рамках определения.
Пусть
;
Определим на
функцию
,
положив:
.
Далее, рассмотрим функцию
,
которая определяется:
;
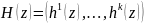И далее, рассмотрим композицию:
.
Для любых
мы имеем равенство:
.
Далее,
.
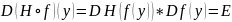Поскольку ранг единичной матрицы в
данном случае равен
,
условие достигнуто.
Теорема доказана.