
- •1) Евклидово n-мерное пространство.
- •2) Подмножества в евклидовом пространстве.
- •3) Функции и непрерывность.
- •6) Правила дифференцирования скалярных функций.
- •7) Частные производные.
- •8) Непрерывно дифференцируемые функции.
- •9) Обратная функция.
- •10) Неявные функции.
- •11) Производные и дифференциалы высших порядков.
- •12) Интеграл по параллелепипеду.
- •13) Мера и объем 0.
- •14) Интегрируемые функции.
- •15) Свойства кратного интеграла.
- •16) Теорема Фубини.
- •17) Разбиение единицы.
- •18) Несобственные интегралы.
- •22) Поля и формы в пространстве.
- •23) Потенциал.
- •24) Теорема Стокса.
- •25) Поверхности.
- •27) Теорема Стокса для ориентированной поверхности
- •28) Элемент площади и площадь поверхностей.
14) Интегрируемые функции.
Лемма
11.3: Пусть – замкнутый параллелепипед и функция
– замкнутый параллелепипед и функция
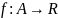 ограничена. Если для любого значения
выполняется неравенство:
ограничена. Если для любого значения
выполняется неравенство:
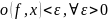 .
То существует разбиение
параллелепипеда
,
для которого выполняется неравенство:
.
То существует разбиение
параллелепипеда
,
для которого выполняется неравенство:
 .
.
Док-во:
Поскольку для любого значения
выполняется неравенство:
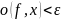 ,
существует некоторый замкнутый
параллелепипед
,
существует некоторый замкнутый
параллелепипед
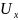 ,
содержащий точку
в своей внутренности, такой, что для
него выполняется неравенство:
,
содержащий точку
в своей внутренности, такой, что для
него выполняется неравенство:
 .
Поскольку
– множество компактное, существует
конечное число параллелепипедов
.
Поскольку
– множество компактное, существует
конечное число параллелепипедов
 ,
покрывающих множество
.
Пусть
– такое разбиение параллелепипеда
,
каждый сегмент
которого, целиком лежит внутри
,
покрывающих множество
.
Пусть
– такое разбиение параллелепипеда
,
каждый сегмент
которого, целиком лежит внутри
 .
Очевидно, что:
.
Очевидно, что:
 .
.
 .
.
Лемма доказана.
Теорема
12.1:
Функция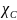 интегрируема
на
тогда
и только тогда, когда граница множества
интегрируема
на
тогда
и только тогда, когда граница множества имеет меру 0. Док-во: Предположим, что
– некоторая внутренняя точка множества
.
Тогда она входит в
вместе с некоторым замкнутым
параллелепипедом. Тогда, очевидно, что
функция
непрерывна и обращается в единицу. Пусть
теперь точка
принадлежит внешности множества
.
Тогда найдется параллелепипед, который
лежит вне
.
На этом параллелепипеде
принимает значение 0 и, также непрерывна.
Рассмотрим ситуацию, когда
принадлежит границе
.
В этом случае, какой бы параллелепипед,
содержащий точку
мы не взяли, в этом параллелепипеде
найдутся точки как принадлежащие
,
так и не принадлежащие. Очевидно, что в
этом случае
является точкой разрыва функции
.
Таким образом, множество точек разрыва
совпадает с границей
имеет меру 0. Док-во: Предположим, что
– некоторая внутренняя точка множества
.
Тогда она входит в
вместе с некоторым замкнутым
параллелепипедом. Тогда, очевидно, что
функция
непрерывна и обращается в единицу. Пусть
теперь точка
принадлежит внешности множества
.
Тогда найдется параллелепипед, который
лежит вне
.
На этом параллелепипеде
принимает значение 0 и, также непрерывна.
Рассмотрим ситуацию, когда
принадлежит границе
.
В этом случае, какой бы параллелепипед,
содержащий точку
мы не взяли, в этом параллелепипеде
найдутся точки как принадлежащие
,
так и не принадлежащие. Очевидно, что в
этом случае
является точкой разрыва функции
.
Таким образом, множество точек разрыва
совпадает с границей
 .
Отсюда следует утверждение теоремы.
.
Отсюда следует утверждение теоремы.
Теорема доказана.
15) Свойства кратного интеграла.
Определение кратного интеграла совершенно аналогично определению определенного интеграла Римана, поэтому его свойства повторяют свойства интеграла по отрезку.
Теорема
: Пусть
–
ограниченное, измеримое по Жордану
множество, и
 – интегрируемые на
функции, для каждого
удовлетворяющие неравенству:
– интегрируемые на
функции, для каждого
удовлетворяющие неравенству:
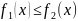 .
Тогда:
.
Тогда:
 .
.
Док-во:
Предположим сначала, что
 –замкнутый
параллелепипед, и
– произвольное его разбиение. Для любого
сегмента
этого разбиения, очевидно, выполняется
неравенство:
–замкнутый
параллелепипед, и
– произвольное его разбиение. Для любого
сегмента
этого разбиения, очевидно, выполняется
неравенство:
 .
Поэтому
.
Поэтому
 ,
откуда:
,
откуда:
 .
Поскольку последнее неравенство
выполнено для любого разбиения
,
то:
.
Поскольку последнее неравенство
выполнено для любого разбиения
,
то:
 .
Тем самым, неравенство 8 установлено
для случая, когда
–замкнутый
параллелепипед. Пусть теперь
– ограниченное, измеримое по Жордану
множество, расположенное в замкнутом
параллелепипеде
.
Тем самым, неравенство 8 установлено
для случая, когда
–замкнутый
параллелепипед. Пусть теперь
– ограниченное, измеримое по Жордану
множество, расположенное в замкнутом
параллелепипеде
 .
Доопределим функции
.
Доопределим функции
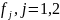 тождественным нулем на множестве
тождественным нулем на множестве
 .
Очевидно, функции
.
Очевидно, функции
 интегрируемы на
,
и для каждого
интегрируемы на
,
и для каждого
 выполняется неравенство:
выполняется неравенство:
 .
Следовательно,
.
Следовательно,
 .
.
Теорема доказана.
Теорема
о замене переменной в кратном интеграле:
Пусть
-открытое
множество, и
 –такая взаимно однозначная функция,
что:
–такая взаимно однозначная функция,
что:
 .
Тогда:
.
Тогда:
 ,
для любой интегрируемой функции
,
для любой интегрируемой функции
 .
.
16) Теорема Фубини.
Теорема
Фубини : Пусть
и
 –замкнутые
параллелепипеды, и пусть функция
–замкнутые
параллелепипеды, и пусть функция
 интегрируема. Также, пусть функция
интегрируема. Также, пусть функция
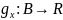 определена по правилу:
определена по правилу:
 .
И далее, определим функции:
.
И далее, определим функции:
 ;
;
 .
Тогда функции
.
Тогда функции
 и
и
 интегрируемы на параллелепипеде
и имеют место равенства:
интегрируемы на параллелепипеде
и имеют место равенства:
 ;
;
 .
.
Док-во:
Рассмотрим
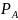 – разбиение параллелепипеда
,
с сегментами
– разбиение параллелепипеда
,
с сегментами
 и
и
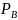 – разбиение
с
сегментами
– разбиение
с
сегментами
 .
Разбиения
и
,
совместно, порождают разбиение
параллелепипеда
.
Сегментами этого разбиения являются
параллелепипеды вида:
.
Разбиения
и
,
совместно, порождают разбиение
параллелепипеда
.
Сегментами этого разбиения являются
параллелепипеды вида:
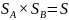 .
Далее, имеем:
.
Далее, имеем:
 ;
Теперь заметим, что для любого
;
Теперь заметим, что для любого
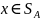 верно:
верно:
 .
Поэтому:
.
Поэтому:
 .
Приведенное неравенство справедливо
для любого
.
Отсюда получается:
.
Приведенное неравенство справедливо
для любого
.
Отсюда получается:
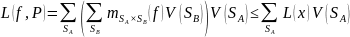 Таким образом:
Таким образом:
 .
Данное неравенство может быть продолжено:
.
Данное неравенство может быть продолжено:
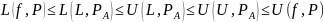 .
Последнее неравенство доказывается
как и первое. Поскольку функция
интегрируема на
,
супремум ее нижних сумм Дарбу будет
равен:
.
Последнее неравенство доказывается
как и первое. Поскольку функция
интегрируема на
,
супремум ее нижних сумм Дарбу будет
равен:
 ;
Отсюда получается:
;
Отсюда получается:
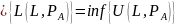 .
Таким образом, получается что функция
.
Таким образом, получается что функция
 интегрируема и верно равенство:
интегрируема и верно равенство:
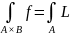 .
Равенство 13.6 установлено. Для функции
получаем аналогичный результат:
.
Равенство 13.6 установлено. Для функции
получаем аналогичный результат:
 .
Таким образом,
– интегрируема.
.
Таким образом,
– интегрируема.
Теорема доказана.
