11) Производные и дифференциалы высших порядков.

Производным отображением порядка или -м дифференциалом отображения в точке называется отображение, касательное в этой точке к производному отображению порядка 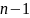от . Таким образом: . Дифференциал функции порядка обозначается: . Тогда: .

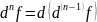Теорема : Если для отображения форма определена, то она симметрична относительно любой пары точек своих аргументов. Док-во: Пусть 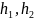– два произвольных фиксированных вектора пространства . Поскольку открыто в , при всех достаточно близких к нулю значениях определена следующая вспомогательная функция: 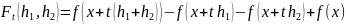. Рассмотрим еще одну вспомогательную функцию: , заведомо определенную для векторов , коллинеарных вектору и таких, что . Заметим, что: . Заметим также, что коль скоро функция в точке имеет второй дифференциал она обязана быть дифференцируема по крайней мере в некоторой окрестности точки . Мы будем считать, что параметр настолько мал, что аргументы в правой части определяющего функцию 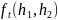равенства лежат в указанной окрестности точки . Воспользуемся этими замечаниями и следствием теоремы о конечном приращении в следующих выкладках: . По определению производного отображения можно записать: . . Учитывая это, предыдущую выкладку можно продолжить и после арифметических упрощений получить: . Но это равенство означает: 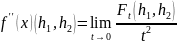. Поскольку очевидно, , то отсюда уже следует: .

Теорема доказана.

12) Интеграл по параллелепипеду.

Разбиением отрезка называется последовательность вещественных чисел таких, что . По аналогии с этим вводится определение для параллелепипеда. В общем случае, для параллелепипеда , если разбивает отрезок на частей …, разбивает отрезок на частей, то параллелепипед разбит на параллелепипедов. Каждый такой параллелепипед будем называть сегментом разбиения . Стоит сказать, что при любом разбиении , верно неравенство: . Лемма 10.2: Для любых двух разбиений верно неравенство: .

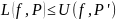Док-во: Рассмотрим продолжение разбиений и : . Например, его можно построить таким образом: . Имеем неравенство: . Лемма доказана.

Теорема 10.3: Функция 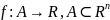, ограниченная в параллелепипеде интегрируема в нем тогда и только тогда, когда для любого значания существует такое разбиение параллелепипеда , при котором выполняется неравенство: .

Док-во: Если выполнено неравенство из теоремы, то, очевидно, что в неравенстве 10.2 имеет место равенство и функция интегрируема. Достаточность установлена. Необходимость. Пусть – интегрируемая функция. Значит, в неравенстве 10.2 имеет место равенство. Из свойств супремума и инфинума следует, что существуют разбиения , такие, что: . Рассмотрим разбиение , являющееся продолжением разбиений и . Для этого разбиения тем более выполняется равенство: .

Теорема доказана.

13) Мера и объем 0.

Говорят, что множество имеет меру 0 если для любого существует такое покрытие множества замкнутыми прямоугольниками , суммарный объем которых удовлетворяет условию: . Легко видеть, что это определение можно также сформулировать для открытых прямоугольников.

Теорема 10.3: Пусть , где – множество меры 0. Если в этом объединении присутствует конечное или счетное число слагаемых, то множество имеет меру 0.

Док-во: Поскольку множество имеет меру 0, для него существует покрытие замкнутыми прямоугольниками, суммарный объем которых удовлетворяет неравенству: . В силу определения множества , оно покрывается совокупностью всех прямоугольников, входящих в состав таблицы. Заметим, что следуя стрелкам все эти прямоугольники можно занумеровать в последоватлеьность. При этом очевидно: .

Теорема доказана.

Лемма 11.1:Если вещественные числа 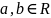удовлетворяют неравенству: , то отрезок не может иметь объем 0. Точнее говоря, для любого конечного покрытия отрезка отрезками 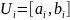имеет место неравенство: 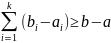. Доказательство леммы очевидно. Из данной леммы следует, что отрезок с положительной длиной, не может иметь меру 0.