
- •1) Евклидово n-мерное пространство.
- •2) Подмножества в евклидовом пространстве.
- •3) Функции и непрерывность.
- •6) Правила дифференцирования скалярных функций.
- •7) Частные производные.
- •8) Непрерывно дифференцируемые функции.
- •9) Обратная функция.
- •10) Неявные функции.
- •11) Производные и дифференциалы высших порядков.
- •12) Интеграл по параллелепипеду.
- •13) Мера и объем 0.
- •14) Интегрируемые функции.
- •15) Свойства кратного интеграла.
- •16) Теорема Фубини.
- •17) Разбиение единицы.
- •18) Несобственные интегралы.
- •22) Поля и формы в пространстве.
- •23) Потенциал.
- •24) Теорема Стокса.
- •25) Поверхности.
- •27) Теорема Стокса для ориентированной поверхности
- •28) Элемент площади и площадь поверхностей.
9) Обратная функция.
Теорема
об обратной функции (7.2):
Пусть функция
непрерывно дифференцируема на некотором
открытом множестве содержащем точку
и пусть при этом ее производная в этой
точке равна нулю. Тогда существует
множество
 ,
содержащее точку
,
такое, что функция
,
действующая из
в
,
содержащее точку
,
такое, что функция
,
действующая из
в
 взаимно однозначна и имеет обратную
функцию
взаимно однозначна и имеет обратную
функцию ,
дифференцируемую на
.
При этом выполняется равенство:
,
дифференцируемую на
.
При этом выполняется равенство:
 .
.
Док-во:
Обозначим через
 линейное отображение:
линейное отображение:
 ,
совпадающее с дифференциалом функции
.
Заметим, что если теорема верна для
функции
,
совпадающее с дифференциалом функции
.
Заметим, что если теорема верна для
функции
 ,
то она верна и для функции
и при этом:
,
то она верна и для функции
и при этом:
 .Воспользуемся
тем, что функция
дифференцируема в точке
.
.Воспользуемся
тем, что функция
дифференцируема в точке
.
 .
Отсюда вытекает неравенство:
.
Отсюда вытекает неравенство: .
Поскольку
.
Поскольку
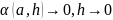 то мы можем выбрать такой параллелепипед
,
содержащий точку
в своей внутренности, чтобы:
то мы можем выбрать такой параллелепипед
,
содержащий точку
в своей внутренности, чтобы:
 .
Из этих рассуждений следует, что в этом
параллелепипеде выполняется неравенство:
.
Из этих рассуждений следует, что в этом
параллелепипеде выполняется неравенство:
 ;
Кроме того, мы можем считать, что в
параллелепипеде
выполняется неравенство:
;
Кроме того, мы можем считать, что в
параллелепипеде
выполняется неравенство:
 ;
;
 ;
Заметим, что поскольку
;
Заметим, что поскольку
 – единичная матрица,
– единичная матрица,
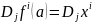 .
Значит последнее соотношение можно
переписать в виде:
.
Значит последнее соотношение можно
переписать в виде:
 ;
Для функции
;
Для функции
 мы получаем неравенство:
мы получаем неравенство:
 .
Из этого получаем:
.
Из этого получаем: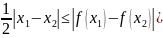 ).
Рассмотрим множество
всех точек
).
Рассмотрим множество
всех точек
 ,
таких, что
,
таких, что
 :
:
 .
Заметим, что если
.
Заметим, что если
 то выполняется неравенство:
то выполняется неравенство: .
Теперь докажем, что для каждого
существует единственная точка
.
Теперь докажем, что для каждого
существует единственная точка
 такая, что:
такая, что:
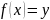 .
С этой целью рассмотрим функцию:
.
С этой целью рассмотрим функцию:
 .
Докажи дифференцируемость функции
.
Докажи дифференцируемость функции
 на множестве
.
Для этого воспользуемся дифференцируемостью
функции
на множестве
.Дадим
приращение:
на множестве
.
Для этого воспользуемся дифференцируемостью
функции
на множестве
.Дадим
приращение: .
Тогда:
.
Тогда:
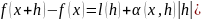 ).
Здесь,
).
Здесь,
 – линейное отображение. Рассмотрим
обратное линейное отображение
– линейное отображение. Рассмотрим
обратное линейное отображение
 .
Применим его к обеим частям равенства
8.3. При этом:
.
Применим его к обеим частям равенства
8.3. При этом:
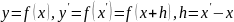 ;
Учтем, что:
;
Учтем, что:
 .
Получим:
.
Получим:
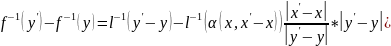 ).
Равенство 8.4 означает дифференцируемость
функции
).
Равенство 8.4 означает дифференцируемость
функции
 в точке
в точке
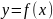 .
А поскольку
– произвольная точка пространства
,
то
– произвольная точка пространства
.
Остается заметить, что функция
совпадает с
– линейным отображением, обратным
отображению
.
Поэтому матрица
.
А поскольку
– произвольная точка пространства
,
то
– произвольная точка пространства
.
Остается заметить, что функция
совпадает с
– линейным отображением, обратным
отображению
.
Поэтому матрица
 совпадает с матрицей, обратной матрице
отображения
совпадает с матрицей, обратной матрице
отображения
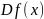 :
:
 .
.
Теорема доказана.
10) Неявные функции.
Рассмотрим
функцию
 ,
определенную равенством:
,
определенную равенством:
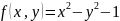 .
И пусть
.
И пусть
 – точка на плоскости
,
удовлетворяющая равенству:
– точка на плоскости
,
удовлетворяющая равенству:
 .
При условии:
.
При условии:
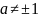 существуют интервалы
существуют интервалы
 ,
обладающие тем свойством, что для каждого
,
обладающие тем свойством, что для каждого
 существует единственное значение
существует единственное значение
 такое, что
такое, что
 .
Тем самым получена однозначная функция
.
Тем самым получена однозначная функция
 ,
определенная равенством:
,
определенная равенством:
 ,
такая, что:
,
такая, что:
 .
Если
.
Если
 то функция имеет вид:
то функция имеет вид: .
Такая функции дифференцируемая на
множестве
и называется неявной. Теорема о неявной
функции (9.1): Пусть функция
.
Такая функции дифференцируемая на
множестве
и называется неявной. Теорема о неявной
функции (9.1): Пусть функция
 непрерывно дифференцируема на некотором
открытом множестве, содержащем точку
непрерывно дифференцируема на некотором
открытом множестве, содержащем точку
 и
.
Если матрица
и
.
Если матрица
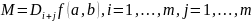 невырожденная (
невырожденная ( ),
то существуют открытые множества
),
то существуют открытые множества
 и
и
 , такие, что для каждого значения
существует единственное значение
, такие, что для каждого значения
существует единственное значение
 ,
для которого выполняется равенство:
.
При этом функция
– дифференцируема.
,
для которого выполняется равенство:
.
При этом функция
– дифференцируема.
Док-во:
Определим функцию
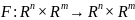 следующим равенством:
следующим равенством:
 .
Заметим, что:
.
Заметим, что: .
.
 .
Функция
.
Функция
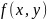 удовлетворяет условиям теоремы об
обратной функции. По этой теореме,
существует открытое множество, содержащее
точку
удовлетворяет условиям теоремы об
обратной функции. По этой теореме,
существует открытое множество, содержащее
точку
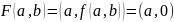 ,
а также открытое множество, содержащее
точку
,
а также открытое множество, содержащее
точку
 ,
причем множество
можно выбрать в виде:
,
причем множество
можно выбрать в виде:
 , таким, что функция
, таким, что функция
 имеет дифференцируемую обратную функцию:
имеет дифференцируемую обратную функцию:
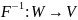 .
При этом очевидно, что:
.
При этом очевидно, что:
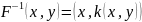 потому что такой же вид имеет прямая
функция. Далее, определим функцию
потому что такой же вид имеет прямая
функция. Далее, определим функцию
 .
Заметим:
.
Заметим:
 .
Далее, имеем:
.
Далее, имеем:
 .
Получено равенство:
.
Получено равенство:
 .
Дифференцируемость функции
.
Дифференцируемость функции
 следует из теоремы об обратной функции.
следует из теоремы об обратной функции.
Теорема доказана.
