1) Евклидово n-мерное пространство.

Евклидовым пространством называется множество всевозможных n-численных последовательностей вещественных чисел 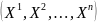. Последовательность называется точкой в пространстве . При этом число называется -й координатой точки. Часто элементы называются векторами, а само пространство векторным пространством. Это следует из того, что над -мерными последовательностями можно определить операции сложения и умножения на число. Линейные векторные пространства имеют размерность . Это значит, что в этом пространстве существует базис из векторов. Обычно выбирается стандартный базис: . Здесь, единица находится в i-й позиции. Выражение называется скалярным или внутренним произведением векторов и кратко записывается: .Таким образом, по определению скалярного произведения, мы имеем: . Скалярное произведение обладает рядом свойств, описываемых теоремой:

Теорема 1.2: Если а также это произвольные векторы пространства , то имеют место свойства:

1) Симметричность: ;

2) Полилинейность: ;

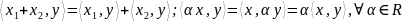3) Положительная определенность: . Равенство достигается в случае, когда ;

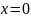4) ;

5) Поляризационное тождество: . Первые четыре пункта очевидны. Докажем пятое равенство.

Док-во: .

Свойство доказано.

2) Подмножества в евклидовом пространстве.

Отрезку на числовой оси есть свой аналог в плоскости – прямоугольник: , который определяется как множество всех пар 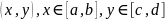. В частности, можно рассматривать замкнутые параллелепипеды вида: . Данная конструкция называется замкнутым параллелепипедом в пространстве . Рассмотрим также открытые параллелепипеды: .Множество 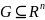называется открытым если каждую свою точку оно содержит в себе с некоторым открытым параллелепипедом (окрестностью). Дополнение к открытому множеству является множеством замкнутым: .

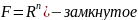Лемма 2.2:Пусть 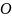– некоторое открытое покрытие рассмотренного выше множества 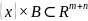. Тогда существует такое открытое множество , содержащее точку , что множество покрывается конечным числом открытых множеств из . Из леммы следует теорема:

Теорема 2.1:Если множества являются компактными, принадлежащими пространствам и соответственно, то множество компактно в пространстве .

Док-во: Пусть – произвольное открытое покрытие множества . Для каждой точки 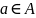рассмотрим множества . Согласно лемме 2.2, для этого множества существует такое открытое множество , что 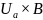покрывается конечным числом открытых множеств из .Очевидно, что открытые множества , покрываюткомпактное множество . Следовательно, существует конечное число множеств покрывающих множество . Множества очевидно, покрывают множество , но каждое из них покрывается конечным числом открытых множеств из . Поэтому этими открытыми множествами из покрывается и множество .

Теорема доказана.

3) Функции и непрерывность.

Функцией , действующей из пространства в пространство называется правило, по которому каждому ставится в соответствие некоторая точка из пространства . Соответствующая точка из обозначается: 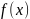. При этом записывается так: . Пусть дана функция . У неё имеется координатных функций: . Эти функции определены по правилу: . В таком случае, называется вектор-функцией. Наоборот, если имеются координатных функций: , то из них можно составить вектор функцию по правилу: .В качестве простейшей функции можно рассмотреть тождественное отображение: . Определим её координатную функцию: . Такая функция называется проецированием. Функция называется непрерывной в точке 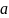если её предел в этой точке равен . Функция называется непрерывной на множестве если она непрерывна в каждой точке этого множества. Из сказанного вытекает теорема:

Теорема 3.1: Пусть . Функция непрерывна на множестве тогда и только тогда, когда для каждого открытого множества существует открытое множество такое, что .

Док-во: Пусть функция непрерывна и . Тогда . Поскольку – открытое множество, точка принадлежит ему вместе с некоторой окрестностью . Так как функция непрерывна в точке , существует такая окрестность 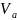точки , что . Далее, рассмотрим открытое множество: . Очевидно, что .

Теорема доказана.

4) Дифференцируемая функция.

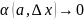Дадим определение функции , дифференцируемой в точке : Функция называется дифференцируемой в точке если верно равенство: . Где – производная функции в точке , – приращение аргумента, а при . Формуле можно придать векторный характер: . Функция называется дифференцируемой в точке если существует такое линейное отображение пространства мерных веторов в пространство мерных векторов, приложенных в точке , для которого выполняется вышесказанное равенство при некоторой функции 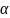, обладающей свойством: .

Теорема 4.1: Если функция дифференцируема в точке , то существует единственная линейная функция удовлетворяющая равенству .

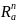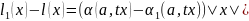Док-во: Предположим, что существует еще одна функция удовлетворяющая равенству: . Тогда: . Пусть – произвольный вектор пространства . Выберем значение и подставим его в предыдущее равенство. В силу линейности, можно сократить: . и 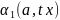здесь стремятся к нулю при 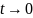, тогда: . Значит, .

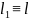Теорема доказана.

Лемма 4.1: Для линейного отображения существует значение , такое, что .

Док-во: В пространстве выберем стандартный базис и разложим вектор по этому базису: . И к этому разложению применим функцию 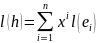. Пусть теперь . Тогда: . .

Лемма доказана.

5) Основные правила дифференцирования.

Теорема о дифференцировании сложной функции(4.2):Если функция дифференцируема в точке 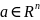, а функция дифференцируема в точке , то сложная функция дифференцируема в точке и выполняется равенство: .

Док-во: Поскольку функция дифференцируема в точке , для нее выполняется равенство: . И так как дифференцируема в точке : 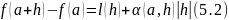В силу леммы 4.1(Для линейного отображения существует значение , такое, что ), из этого следует неравенство: Положим, . Заметим, что в силу (5.3), при 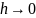. Далее, сделаем преобразования: В силу леммы 4.1: И поэтому: . Это, наряду с неравенством (5.3) позволяет сказать, что выражение в больших скобках представляет собой бесконечно малую функцию и, следовательно, поскольку композиция является линейной, формула 5.4 означает чтофункция дифференцируемаи дифференциал её совпадает с . Очевидно, что тогда выполняется равенство из теоремы.

Теорема доказана.

Теорема 5.1: 1) Если функция является постоянной (существует вектор ), её дифференциал равен нулю . 2) Если 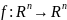– линейное отображение, то эта функция дифференцируема в любой точке и в пространстве . 3) Если функция дифференцируема в точке , то в этой точке дифференцируема каждая ее координатная функция. Верно и обратное. При этом выполняется символическое равенство: . Пункты 1 и 2 очевидны.