Зависимость n2 от ω для случая трёх резонансных частот

Сказанное выше относится к электронам внешних оболочек атомов (оптическим электронам). Именно они взаимодействуют с излучением оптического диапазона. Электроны внутренних оболочек имеют очень высокие собственные частоты, и поле световой волны на них практически не влияет. Данные электроны эффективно взаимодействуют с рентгеновским излучением.

Из рис. 7 видно, что в некоторых областях спектра n<1, или v>c. Это обстоятельство не противоречит специальной теории относительности, основывающейся на утверждении, что скорость передачи сигнала не может превзойти с. Передача сигнала связана с распространением энергии в пространстве. Скорость распространения световой энергии, так называемая групповая скорость u ,отличается от фазовой, характеризующей скорость перемещения поверхности постоянной фазы. Соответствующие расчеты показывают, что групповая скорость оказывается меньше с в области нормальной дисперсии. В области аномальной дисперсии понятие групповой скорости теряет смысл, однако и в данном случае скорость передачи энергии меньше с.

3.Методика выполнения работы

3.1.Определение показателя преломления веществ по углу наименьшего отклонения

Рассмотрим метод определения показателя преломления, применимый для прозрачных веществ. Метод состоит в измерении угла отклонения лучей при прохождении света через призму, изготовленную из исследуемого материала. На призму направляется параллельный пучок лучей, поэтому достаточно рассмотреть ход одного из них (S₁) в плоскости, перпендикулярной линии пересечения преломляющих граней призмы (рис.8).

Ход луча через призму рассчитывается на основании законов преломления света. При преломлении на первой грани призмы АС получим

(14)

где n – показатель преломления материала призмы для данной длины волны света.

Угол падения луча на вторую грань призмы находится из треугольника EDF:

i₂ = φ – r₁ (15)

Угол преломления r₂ можно найти из закона преломления

sin r₂ = n ∙ sin i₂ (16)

Из формул (13), (14), (15) получаем выражение для определения показателя преломления, содержащее углы i₁, r₂, φ, которые можно измерить:

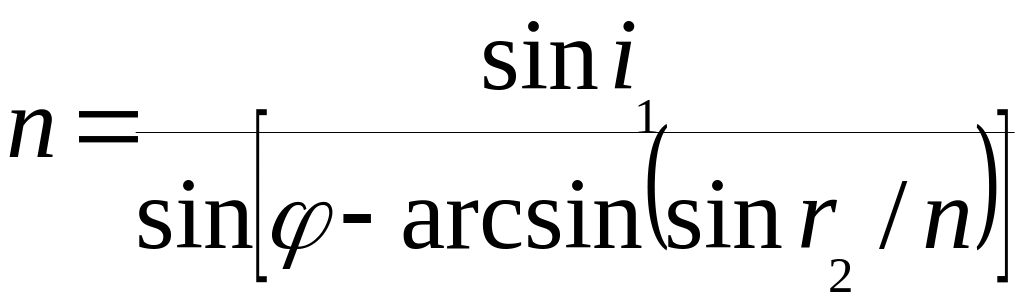₍₁₇₎

Ход лучей в призме

Рис.8. S₁─направление луча, падающего на призму,

S₂─ направление луча, вышедшего из призмы,

А₁─направление нормали к грани, на которую падает луч S₁,

А₂─ направление нормали к грани, из которой выходит луч S₂,

i₁, i₂ - углы падения,

r₁, r₂ - углы преломления на границах раздела АС и АВ соответственно,

φ - преломляющий угол призмы,

δ - угол отклонения выходящего из призмы луча относительно первоначального направления.

Измерения и вычисления упрощаются, а точность определения n возрастает, если сократить число измеряемых углов. Этого можно достигнуть при симметричном ходе лучей через призму, при котором выполняются следующие равенства:

i₁ = r₂ , r₁ = i₂ (18)

На практике вместо углов i₁, r₂ удобнее измерять угол отклонения лучей от своего первоначального направления δ. Этот угол можно найти из рассмотрения четырёхугольника НFDЕ. Действительно, так как угол HED = i₁ = r₂ = углу HFD, то сумма углов четырёхугольника равна:

2π = (π - δ) + (π - φ) + i₁+ r₂ (19)

Из выражения (17) для симметричного хода лучей получаем:

i₁ = (δ + φ) / 2 , (20)

а из выражения (14) имеем

r₁ = φ / 2 . (21)

Подставляя в формулу (14) значения i₁ и r₁ из (20) и (21), получим формулу для определения показателя преломления при симметричном ходе лучей через призму:

⁽²²⁾

Можно показать, что при симметричном ходе лучей угол отклонения будет наименьшим. Таким образом, добиваясь минимального отклонения лучей призмой, мы тем самым устанавливаем призму симметрично по отношению к падающему и выходящему лучам.

Следовательно, определение показателя преломления вещества сводится к измерению преломляющего угла призмы и угла наименьшего отклонения лучей.