Обусловленность матрицы

Рассмотрим вопрос об устойчивости решения относительно изменения элементов матрицы.

Теоретическое решение системы  дается формулой  ,

где  - матрица, обратная к  . Обратную матрицу называют устойчивой, если малым изменениям в элементах матрицы соответствуют малые изменения в элементах обратной матрицы. Очевидно, что необходимым условием устойчивости обратной матрицы является то, чтобы определитель матрицы не был бы близок к нулю. Но это условие не является достаточным. В качестве меры близости к вырожденности матрицы  рассматривают числа обусловленности:

,

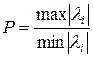где  - собственное значение матрицы  ; и  .

Матрицу называют плохо обусловленной, если соответствующая ей обратная матрица неустойчива.

Чем больше числа обусловленности, тем хуже обусловленность матрицы.

На практике этим определением обусловленности воспользоваться достаточно трудно, т.к. это связано с нахождением обратной матрицы и собственных значений матрицы. Поэтому обычно ограничиваются проверкой условия  . Для этого систему нормируют, т.е.  -е уравнение системы делят на величину 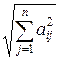 , а затем определитель полученной матрицы сравнивают с единицей. Малость указанного определителя по сравнению с единицей является признаком плохой обусловленности системы.

25. Приближенное вычисление интеграла. Метод прямоугольников

Многие инженерные задачи, задачи физики, геометрии и многих других областей человеческой деятельности приводят к необходимости вычислять определенный интеграл вида

, (1),

где f(x) — подынтегральная функция, непрерывная на отрезке [а; b].

Пусть задана подынтегральная функция f(х), необходимо найти определенный интеграл, который вычисляется по форму­ле Ньютона — Лейбница

= F(b)-F(a). (2)

Если же интеграл от данной функции не может быть вычислен по формуле (2), или если функция f(х) задана графически или таблицей, то для вычисления определенного интеграла применяют приближенные формулы. Для приближенного вычисления инте­грала (2) существует много численных методов, таких как:

• метод прямоугольников;

• трапеций;

• Симпсона и др.

При вычислении интеграла следует помнить, каков геомет­рический смысл определенного интеграла.

*

Если f(x) ≥ 0 на отрезке [а; b], то  численно равен площади фигуры, ограниченной графиком функции y=f(x), от­резком оси абсцисс, прямой х= а и прямой х= b(рис. 1). Та­ким образом, вычисление интеграла равносильно вычислению площади криволинейной трапеции.

Рис. 1. Геометрический смысл интеграла

Разделим отрезок [а; b]на п равных частей, т. е. на п эле­ментарных отрезков. Длина каждого элементарного отрезка  .

Точками деления будут: х0 = а; х1 = а + h; х2 = a + 2h, ..., ; хn-1 = a + (n-1)h; хn = b. Эти числа будем называть узлами. Вы­числим значения функции f(x) в узлах, обозначим их у0, у1, у2, ..., уn. Стало быть, y0=f(a), у1 =f(x1), у2=f(x2),..., yn=f(b). Числа у0, у1, у2, ..., уn являются ординатами точек графи­ка функции, соответствующих абсциссам х0, х1, х2, ..., хn (рис. 2).

Рис. 2. Методы левых (а) и правых (б) прямоугольников

Из рис. 2. видно, что площадь криволинейной трапеции приближенно заменяется площадью многоугольника, составлен­ного из п прямоугольников. Таким образом, вычисление опреде­ленного интеграла сводится к нахождению суммы n элементар­ных прямоугольников

 

(3)

Формула (3) называется формулой левых прямоугольни­ков, (4) — правых прямоугольников, (5) — формулой сред­них прямоугольников (рис. 3).

 (5)

 

Рис. 3. Метод средних прямоугольников

 

Алгоритм вычисления интеграла по формуле левых прямо­угольников показан на рис. 4.

Рис. 4. Схема алгоритма вычисления интеграла

25. Приближенный метод решения интегралов.

Метод прямоугольников (правых, средних, левых).

Многие инженерные задачи, задачи физики, геометрии и многих других областей человеческой деятельности приводят к необходимости вычислять определенный интеграл вида где f(x) -данная функция, непрерывная на отрезке [a; b]. Если неопределенный интеграл данной функции мы найти не умеем, или по какой-либо причине не хотим воспользоваться формулой Ньютона-Лейбница или если функция f(x) задана графически или таблицей, то для вычисления определенного интеграла применяют приближенные формулы. Для приближенного вычисления интеграла можно использовать метод прямоугольников. При вычислении интеграла следует помнить, каков геометрический смысл определенного интеграла. Если f(x)>=0 на отрезке [a; b], то  численно равен площади фигуры, ограниченной графиком функции y=f(x), отрезком оси абсцисс, прямой x=a и прямой x=b (рис. 1.1) Таким образом, вычисление интеграла равносильно вычислению площади криволинейной трапеции

Разделим отрезок [a; b] на n равных частей, т.е. на n элементарных отрезков. Длина каждого элементарного отрезка  .Строим прямоугольники. Это можно делать несколькими способами:

Ле вые прямоуголики (слева на право)

Правые прямоугоники (построение справа на лево)

Средние прямоугольники (посредине)

Из рис. 1.2 следует, что площадь криволинейной трапеции приближенно заменяется площадью многоугольника, составленного из n прямоугольников. Таким образом, вычисление определенного интеграла сводится к нахождению суммы n элементарных прямоугольников.

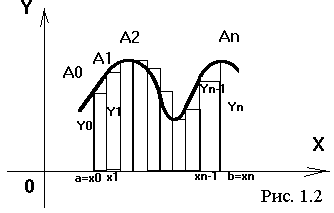
Формула средних прямоугольников.

Sсредих= (Sправых + Sлевых) /2

(1.5)

26. Метод трапеций. Идея аналогична. Отрезок интегрирования разбивается на несколько промежуточных отрезков, и график подынтегральной функции приближается ломаной линией:

Таким образом, наша площадь приближается суммой площадей трапеций (красный цвет). метод трапеций даёт значительно лучшее приближение, чем метод прямоугольников (при одинаковом количестве отрезков разбиения). И, естественно, чем больше более мелких промежуточных отрезков мы рассмотрим, тем будет выше точность.

Рассмотрим определенный интеграл  , где   – функция, непрерывная на отрезке  .  Проведём разбиение отрезка   на   равных отрезков: . При этом, очевидно:   (нижний предел интегрирования) и   (верхний предел интегрирования). Точки   также называютузлами.

Тогда определенный интеграл можно вычислить приближенно по формуле трапеций: 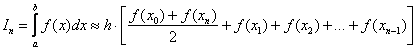, где:  – длина каждого из маленьких отрезков или шаг;  – значения подынтегральной функции в точках 

27. Метод Симпсона (метод парабол). Это более совершенный способ – график подынтегральной функции приближается не ломаной линией, а маленькими параболками. Сколько промежуточных отрезков – столько и маленьких парабол. метод Симпсона даст ещё более точное приближение, чем метод прямоугольников или трапеций. Рассмотрим определенный интеграл  , где   – функция, непрерывная на отрезке  .  Проведём разбиение отрезка   на чётное количество равных отрезков. Чётное количество отрезков обозначают через  .Итак, наше разбиение имеет следующий вид:

Термины аналогичны терминам метода трапеций: Точки   называют узлами.

Формула Симпсона для приближенного вычисления определенного интеграла имеет следующий вид: 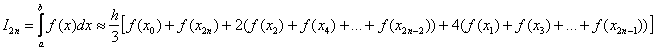где:  – длина каждого из маленьких отрезков или шаг;  – значения подынтегральной функции в точках  .

Детализируя это нагромождение, разберу формулу подробнее:  – сумма первого и последнего значения подынтегральной функции;  – сумма членов с чётными индексами умножается на 2;  – сумма членов с нечётными индексами умножается на 4.