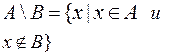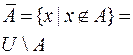Множества

1.

а) Множеством называется совокупность некоторых элементов, объединенных каким-либо общим признаком. 

б) Мощность множества — характеристика множеств , обобщающая понятие количества элементов конечного множества.

В) Рассмотрим операции над множествами, которые позволяют из уже имеющихся множеств образовывать новые множества.

Для любых двух множеств   и   определены новые множества, называемые объединением, пересечением, разностью и симметрической разностью:

 — объединение,  — пересечение,  — разность,  — симметрическая разность,

г) Диаграмма Венна (как правило, общепринятое название - диаграмма Эйлера — Венна) — схематичное изображение всех возможных пересечений нескольких (часто — трёх) множеств.

Название операции	Обозначение	Изображение	Определение	Символическая запись	Лог. операции
Пересечение множеств			Те и только те элементы, которые принадлежат одновременно А и В		Λ
Объединение множеств			Те и только те элементы, которые принадлежат хотя бы одному из множеств А или В		V
Разность множеств			Те и только те элементы, которые не принадлежат В
Дополнение к множеству А			Те и только те элементы, которые не принадлежат А (т.е. дополняют его до универсального U)
Симметрическая разность			Те и только те элементы, которые принадлежат одному из множеств: А либо В, но не являются общими элементами

2.

Табличный способ задания логической функции

Таблица 2.1 – Таблица истинности функции 4 – х переменных

х1	х2	х3		х4	F

Наборы могут обозначаться десятичными или шестнадцатеричными числами. Для нашей таблицы: 2, 4, 7, 8, 9, 10, 12, 13,15 или 2, 4, 7, 8, 9, A, C, D, F.

Таблица 2.1 называется таблицей истинности.

Число двоичных наборов от количества переменных находится в следующей зависимости:

2ⁿ ,

где n – число переменных.

Примечание: недостаток табличного представления булевой функции: при увеличении числа переменных размер таблицы резко увеличивается.

Это - частный способ табличного представления логических функций. В частности – карты Карно.

Таблица 2.2 – Матричный способ представления

3.

Булеан

 

Множество всех подмножеств множества М называется булеаном и обозначается 2^М:

2^М: = А  А  М.

 

 

ТЕОРЕМА          

Для конечного множества М  2^М  = 2^М .

 

 

Доказательство

 

Индукция по М. База: если М = 0, то М =  и 2^ = . Следовательно, 2^ =  =1 = 2⁰ = 2^.

Индукционный переход: пусть М М < k  2^М = 2^М. Рассмотрим М = а₁,…, а_k , М = k. Положим

М₁: = Х  2^М  а_k  Х и М₂: = Х  2^М  а_k  Х.



 Имеем 2^М = М₁ U М₂  и М₁ ∩ М₂ = . По индукционному предположению М₁ = 2^k –1, М₂ = 2^k –1. Следовательно, 2^М = М₁ + М₂ = 2^k  -1 + 2^k –1 = 2 ∙ 2^k –1 = 2^k = 2^М.

 

Пересечение, объединение и разность подмножеств множества U (универсума) являются подмножествами множества U. Множество всех подмножеств множества U с операциями пересечения, объединения, разности и дополнения образует алгебру подмножеств множества U.

4.

1. Коммутативность объединения	1’. Коммутативность пересечения
2. Ассоциативность объединения	2’. Ассоциативность пересечения
3. Дистрибутивность объединения относительно пересечения	3’. Дистрибутивность пересечения относительно объединения
4. Законы действия с пустым и универсальным множествами	4’. Законы действия с пустым и универсальным множествами
5. Закон идемпотентности объединения	5’. Закон идемпотентности пересечения
6. Закон де Моргана	6’. Закон де  Моргана
7. Закон поглощения	7’. Закон поглощения
8. Закон склеивания	8’. Закон склеивания
9. Закон Порецкого	9’. Закон Порецкого
10. Закон двойного дополнения

5.

Декартово произведение двух множеств — это множество, элементами которого являются всевозможные упорядоченные пары элементов исходных множеств.

Отношения

6.

а) Отношение - один из способов задания взаимодействия между элементами множества.

б)Бинарные отношения используются для определения взаимосвязей, которыми характеризуются пары элементов множества А и В.

в) Инфиксная нотация — это форма записи математических и логических формул, в которой операторы записаны в инфиксном стиле между операндами на которые они воздействуют .

7.

Обратное отношение: R¯¹={(a,b)|(b,a) принадлежит R};

Дополнение отношения: ͞R={(a,b)|(b,a) не принадлежит R};

Универсальное отношение: U={(a,b)|a принадлежит A, b принадлежит B}.

8.

• Рефлексивность: 

• Антирефлексивность (иррефлексивность): 

• Корефлексивность: 

• Симметричность: 

• Антисимметричность: 

• Асимметричность:  . Асимметричность Транзитивность: 

• Связность: 

9.

1)Отношение R на множество М называется отношением нестрогого порядка, если оно может быть представлено в виде: , где R₁- строгий порядок на М, а Е– диагональное отношение.

2)Отношение R на множестве М называется отношением строгого порядка, если оно антирефлексивно и транзитивно.

3)Отношение порядка  , являющееся полным, то есть таким, что

называется полным порядком.

4) Бинарное отношение   на множестве   называется отношением частичного порядка¹⁾, если оно удовлетворяет свойствам

1. рефлексивности:   для всех  ;

2. антисимметричности:         для всех  ;

3. транзитивности:         для всех  .

• 5)Бинарное отношение   на   называется предпорядком (или квазипорядком), если оно транзитивно и рефлексивно, то есть

  1. 

  2. 

6)Замыканием отношения   относительно свойства   называется такое множество  , что:

1. .

2.  обладает свойством  .

3.  является подмножеством любого другого отношения, содержащего   и обладающего свойством  .

Другими словами,   — минимальное надмножество  , выдерживающее  .

10.

1)Линейный порядок можно определить как слабый порядок, для которого классы безразличия содержат ровно по одному элементу.

2)

а) минимальный элемент — это такой элемент  , что для любого   элементы   и   не сравнимы или  .

б) Элемент   называют максимальным элементом множества  , если для всякого   имеет место одно из двух: или  , или   и   не сравнимы.

3)

Диаграмма Хассе — вид диаграмм, используемый для представления конечного частично упорядоченного множества в виде рисунка его транзитивного сокращения. Конкретно, для частично упорядоченного множества   диаграмма представляет каждый элемент   как вершины на плоскости и отрезки или кривые, идущие вверх от элемента   к элементу  , если   и не существует элемента  , для которого  . Эти кривые могут пересекаться, но не должны проходить через вершины, если только они не являются концами линии. Такая диаграмма с помеченными вершинами однозначно определяют частичный порядок.

11. Соответствие между множествами. Свойства соответствий: область определения, область значений, сечения.

Пусть есть два множества А={1,2,3} и B={a,b}. Обычное умножение этого кала даст нам шесть элементов в сумме: А х В = {(1.а)(1.b)(2.a)(2.b)(3.a)(3.b)} и эта загогулина будет иметь 2^6 различных подмножеств. И любое из этих подмножеств называется СООТВЕТСВИЕМ (обозн. буквой G). Вот так просто

Область определения соотвествия (или первая проекция):

Dom G = np₁G={x|(x,y) ∈ G}

(символ Dom означает – Domain – область)

Область значений соответствия (или вторая проекция):

Im G =np₂G={y|(x,y) ∈G}

(Im – Image – образ)

Сечение соответствия G по элементу X₀:

G|_x0={y|(x₀,y) ∈G}

Если нужно но Y₀ то меняем y из формулы выше на х

12. Способы задания соответствий: граф соответствия, булевы матрицы.

Соответствие – это тоже множество, и его можно задавать как и все множества перечислением элементов. Но еще есть способы: матрица и граф соответствия.

Пускай есть X={x,y,z} и Y={a,b} и возьмем рандомное (а согл. 11 Соотвествие – это любое множество из образованного после умножения двух множеств) соответствие которое равно G={(x,a),(x,b),(z,a)}

И вся суть графического отображения состоит в НАНЕСЕНИИ точек Соотв. Элементам множеств (а б х у z) и создание направл. графов в том случае, если они образуют пару

А еще можно в виде матрицы задать – где 0 это не пересекается, 1 – пересекается

Такие матрицы зовутся БУЛЕВЫМИ (1 или 0).Сами матрицы можно перемножать и складывать как завещал нурлан (по законам алгебры), однако элементы уже нужно через различные логические операции херачить – типо Конъюнкции или Дизъюнкции. И тут надо различать ЛОГИЧЕСКАЯ операция над матрицами или АЛГЕБРАИЧЕСКАЯ

13. Отображения. Образы и прообразы элементов.

Соответствие G ⊂ X x Y называется отображением, если область определения соотвествия совпадает с множеством X (Dom G=X или np₁ G=X). Отображение зовется функциональным, если любое сечение содержит только 1 элемент.

Если G – функциональное соответствие, то сечение G|_x0 называют образом элемента Х₀∈Х, а сечение G|_y0 называют прообразом элемента y₀=Y

Определение (по мне так попроще) с инета:

Пусть даны два множества X и Y. Такое соответствие, при котором каждому элементу  соответствует (единственный) элемент , называется отображением множества X в множество Y; в частности, если каждый элемент  соответствует по крайней мере одному элементу , то такое соответствие называется отображением X на Y.

     Если элементу x соответствует y, то y называется образом элемента x, а x - прообразом элемента y. Пишут:   или y = f(x). Множество A всех элементов  , имеющих один и тот же образ , называется полным прообразом элемента y.

14 Сюръективные, инъективные и биективные отображения.

Слова страшные, но по сути своей являются свойствами отображений.

Инъективным отображением называется отображение, для которого из неравенства x1 и x2 следует неравенство f(x1) и f(x2). Аналогично можно сказать, что из x1=x2 следует, f(x1)=f(x2). -> различные элементы множества Х должны иметь различные образы

Сюръективным называется отображение, для которого область определения совпадает с множеством значений отображения. Аналогично можно сказать, что полный прообраз не является пустым множеством для любого y из множества значений отображения.-> f сюръективно, если каждый элемент y ∈ Y имеет хоть 1 прообраз.

Биективным отображением называется отображение, обладающее признаками инъективности и сюръективности одновременно.

15 Композиция отображений. Транзитивное замыкание отображений

Пусть f – отображение множества A в множество B, g – отображение множества B в множество C. Композицией отображений f  и g называется отображение

h = g f,                                                  (1)

которое сопоставляет любому элементу a множества A элемент

h(a) = g(f(a))                                         (2)

множества C. Обратим внимание, что в обозначении операции композиции (1) первое выполняемое отображение пишется справа, второе – слева, что связано с записью (2).

Транзитивное замыкание – если аналогией и по-простому, то представьте, что есть

Медь -> используется в производстве Мат Платы

Экран -> используется в производстве телефона

Мат. Плата. -> используется в производстве телефона

Нигде не сказано, что медь используется в производстве телефона, но раз из него клепаем мат. Плату – соотв можно добавить

Медь -> используется в производстве телефона

Это если коротко и понятно о транзитивных замыканиях

16.

21. Формула Паскаля. Треугольник Паскаля

Биномиальные коэффициенты полезно выстроить в так называемый треугольник Паскаля

Каждая (n + 1)-ая строка этого треугольника состоит из биномиальных коэффициентов, получающихся при раскрытии скобок в выражении

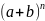
Вычислив несколько первых коэффициентов треугольника Паскаля, мы получим

Так как С(n, 0) = С(n, n) = 1, на внешних сторонах треугольника Паскаля всегда стоят единицы. Симметрия относительно вертикальной высоты треугольника следует из тождества:

С(n, k) = С(n, n — k;),

которое легко доказывается с помощью формулы для С(п^ к). Есть и другие закономерности, которые бросаются в глаза при взгляде на треугольник Паскаля. Например, сложив два последовательных числа, стоящих в строке треугольника, мы получим число из следующей строки, которое стоит между двумя сложенными. Это свойство известно как формула Паскаля:

С(n - 1, k - 1) + С(n - 1, k) = С(n, k), справедливая при О < k < n.

___Дополнительная инфа. Доказательство.________

Доказательство формулы состоит в последовательности преобразований:

22. Алгебраические операции (n-арная). Ранг операции.

4.1. Алгебраические операции и их свойства

Бинарные и n-местные алгебраические операции.

Пусть А – непустое множество.

Определение 4.1. Отображение множества А×А в А называется бинарной алгебраической операцией на множестве А.

Примерами бинарных алгебраических операций являются обычное сложение и умножение на множестве целых чисел, объединение и пересечение на булеане непустого множества.

Определение 4.2. Отображение множества 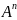в А называется n-арной алгебраической операцией на множестве А, а число n (n ≥ 1) – рангом операции.

Выделение некоторого элемента множества А называется нульарной операцией на множестве А, число 0 – рангом нульарной операции.

Определение 4.3. Частичная функция из множества в А называется частичной n-арной алгебраической операцией на множестве А.

23. Бинарные алгебраические операции (бао): нейтральный и смметричный элементы. Аддитивная и мультипликативная форма записи бао.

Нейтральные элементы

Пусть ∗ – бинарная алгебраическая операция на непустом множестве А.

Определение 4.7. Элемент е ∈ А называется нейтральным относительно операции ∗, если (∀a ∈ А) a ∗ e = e ∗ a = a.

Теорема 4.1. Если нейтральный элемент относительно операции ∗ существует, то он единственен.

Доказательство. Пусть e и e′ – нейтральные элементы относительно операции ∗.

Тогда e = e ∗ e′ = e′, то есть e = e′.

Симметричные элементы

Пусть ∗ есть бинарная алгебраическая операция на непустом множестве А и элемент е ∈ А – нейтральный элемент относительно ∗.

Определение 4.8. Элемент а ′ ∈ А называется симметричным к элементу а ∈ А относительно операции ∗, если а ∗ a' = a ′∗ a = е. В этом случае элемент а называется симметризуемым, а элементы а и а ′ – взаимно симметричными.

Теорема 4.2. Если операция ∗ ассоциативна и элемент a симметризуем, то существует единственный элемент, симметричный к а.

Доказательство. Пусть a ′ , a ″ есть элементы, симметричные к элементу a относительно ∗. Следовательно, a ∗ a ′ = a ′ ∗ a = e и a ∗ a ″ = a ″ ∗ a = e. Тогда в силу ассоциативности операции ∗ получаем a ′ = a ′ ∗ e = a ′ ∗ (a ∗ a ″ ) = (a ′ ∗ a) ∗ a ″ = e ∗ a ″ = a ″ , то есть a ′ = a ″ .

Аддитивная и мультипликативная форма записи бинарной алгебраической операции

Для обозначения бинарной алгебраической операции ∗ наиболее часто используются аддитивная и мультипликативная формы записи.

При аддитивной форме записи операцию ∗ называют сложением, а ее результат a ∗ b – суммой а и b. При этом вместо a ∗ b пишут а + b. Нейтральный элемент относительно сложения называют нулевым элементом (или нулем) и обозначают символом 0.

Элемент, симметричный к элементу а, называют противоположным к элементу а и обозначают через –а.

При мультипликативной форме записи операцию ∗ называют умножением, а ее результат а ∗ b – произведением а и b. При этом вместо а ∗ b пишут a ⋅ b. Нейтральный элемент относительно умножения называют единичным элементом (или единицей) и обозначают символом 1.

Элемент, симметричный к элементу а, называют обратным к элементу а и обозначают через .