3.2.7 Расчет т-образного косоура по трещиностойкости

Момент в расчетном сечении от практически постоянной комбинации равномерно распределенных нагрузок:

равен:

По /16/ для класса X0 предельно допустимая ширина раскрытия трещин .

Геометрические размеры сечения примем равными 400х270мм, толщина защитного слоя-15мм.

_{Арматура класса} S400 ( ). Диаметр продольной арматуры-_{5Ø12мм S400 с , диаметр поперечной арматуры- Ø=4мм с площадью .}

_{Бетон класс} ( модуль упругости 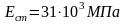(для марки по подвижности П1).

Рабочая высота сечения

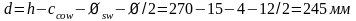
(0,6).

Проверяем ширину раскрытия трещин по упрощенной методике, пользуясь данными /16/. Для сечений прямоугольной формы, армированных арматурой класса S400 при 0,5 1,0 плечо внутренней пары сил определяется:

Z=0,8d=0,8x245=196мм

Напряжение в растянутой арматуре определяем по формуле:

.

По /16/ при и .

Принятый диаметр  .

Проверим ширину раскрытия трещин расчетным путем. Учитывая то обстоятельство, что момент рассчитан на практически постоянной комбинации равномерно распределенных нагрузок, при проверке раскрытия трещин используем эффективный модуль упругости:

.

Предельное значение коэффициента ползучести определим номограммы, приведенной на рис.4.16 /16/. При и  для сут. =1

.

Коэффициент приведения

Для сечений с трещиной при использовании двухлинейонй диаграммы деформирования высота сжатой зоны в общем случае может быть найдена из условия равенства статических моментов сжатой и растянутой зон сечения относительно нейтральной оси:

Тогда

.

При отсутствии расчетной арматуры в сжатой зоне .

.

Подставляя значение получаем:

.

Напряжение в арматуре:

.

Расчетную ширину раскрытия трещин определяем по формуле:

,

где -среднее расстояние между трещинами, определяемое по формуле:

при 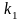=0,8 (для стержней периодического профиля), (при изгибе),

min: 

Средние относительные деформации арматуры определим по формуле:

При (для стержневой арматуры), (для практически постоянной комбинации нагрузок);

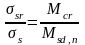
где - момент трещинообразования

,

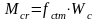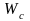- момент сопротивления бетонного сечения

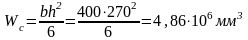
Тогда

Тогда при



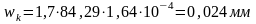
ая

Проверка по ширине раскрытия трещин выполняется.

3.2.8 Расчет т-образного косоура по деформациям

Максимальный прогиб в середине пролета свободно опертого косоура,, загруженного равномерно распределенной нагрузкой:

определим по формуле:

По таблице 11.1 /16/ коэффициент

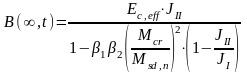
Для прямоугольного сечения

При

,

При и получаем:

Жесткость сечения с трещиной:

Прогиб в середине пролета

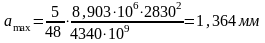
Допустимый прогиб

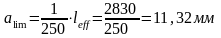2



Максимальный прогиб в середине балки не превышает допустимый, т.е. проверка выполняется.