3.1.5 Расчет и конструирование нижнего пояса фермы

Нижний пояс работает на растяжение. Расчётное продольное усилие в нижнем поясе принимаем по таблице 3.1.3 сочетаний нагрузок:

(3 стержень). Нижний пояс фермы конструируем из стали марки С255. Расчётное сопротивление стали

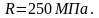
Требуемая площадь сечения нижнего пояса определяем /6, стр.10/:

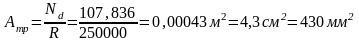
Принимаем два равнополочных уголка 32×4мм (уголок 32×32×4 – ГОСТ_851-86), суммарной площадью .

где, – площадь сечения нижнего пояса .

3.1.6 Расчет и конструирование средней стойки фермы

Растягивающая сила, действующая в среднем стержне (стойке) №15 равна: , взятая из таблицы 3.1.3 сочетания нагрузок КН1, как максимальная сила, действующая в стойках фермы. Т.к. стойка работает на растяжение, то сечение принимается из одиночной стальной арматуры. Принимаем арматуры класса S400 с нарезками на концах. Расчётное сопротивление стали .

Коэффициент концентрации напряжений в нарезке: определяется : .

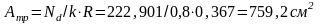В зависимости от полученной площади подбираем диаметр стальной арматуры: диаметр = 32 мм с расчётной площадью .

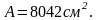Т.к. условие выполняется, следовательно принимаем подобранное сечение стойки.

3.1.7 Расчет и конструирование раскоса фермы

Все раскосы фермы работают на сжатие. Подбирается и проверяется сечение раскоса №19, так как в нём действует наибольшая сжимающая сила:

Длина раскоса №19: .

Расчётная длина раскоса определяется по формуле /4, форм. 3.10/:

где, – коэффициент, учитывающий закрепление элемента и нагрузку, действующую на элемент /4, табл. 3.1/.

Предварительно принимаем сечение раскоса /4, табл. 2.1/. Ширину сечения раскоса принимаем такую же как в верхнем поясе фермы 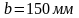, а толщину , в 4 слоя склеенных досок. Тогда высота сечения будет:

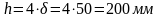
Соответственно, площадь поперечного сечения:

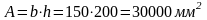
Гибкость раскоса определяем по формуле /4, форм. 3.9/:

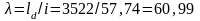
где, - радиус инерции сечения;

= 60,99 не превышает предельную гибкость = приведенной в таблице /5, табл. 7.2/.

В соответствии с /5, п. 7.1.4.2/ элементы с 35 следует проверять на устойчивость:

где, – расчетное сжимающее напряжение, определяемое по формуле 7 /4, форм.3.5/:

– расчётное значение сопротивление сжатию.

/4, табл. 6.5/

– коэффициент продольного изгиба, определяемый в зависимости от гибкости элемента.

При , определяем по формуле /5, форм. 7.14/:

Следовательно, подставив данные в формулу /4, форм. 3.5/ получим:

Условие выполняется, следовательно устойчивость сжатого раскоса обеспечена и принятое сечение оставляем для дальнейших расчетов.

3.2 Расчет и конструирование лестничного марша

3.2.1 Краткое описание конструкции

Лестница представляет собой конструкцию из монолитного железобетона, основными элементами которой являются ступени и Т-образный косоур. Ширина марша – 1500 мм, длина - 2950мм, угол наклона марша – 27^О. Класс бетона , класс арматуры S400, класс по условиям эксплуатации – X0. Толщина защитного слоя 20 мм.

3.2.2 Расчет и конструирование Т-образных косоуров

Т-образный косоур представляет собой балочный элемент, рассчитываемый на изгиб как свободно опертая балка на действующие нагрузки с учетом уклона марша.

Рис.3.2.2 К расчету Т-образного косоура

3.2.2.1. Определение расчетных длин

Расчетный полет l_ef косоура принимаем равным расстоянию между осями его опор (рис.3.2.3.)

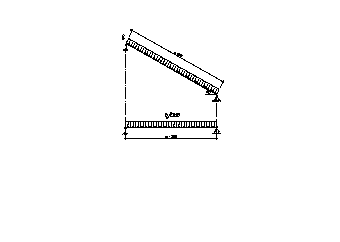
рис.3.2.3. Расчетная схема Т-образного косоура

1) Постоянная нагрузка от собственного веса Т-образного косоура равна:

,

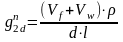где плотность бетона, кг/м³; = 2500 кг/м³ = 25кН/м³;

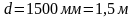
кН/м²